今回はシステムの運動方程式をニュートンの運動方程式以外の方法で求める方法を紹介します。
算出方法は異なりますが、求めた結果は同じになります。
ニュートンの運動方程式でシステムの運動を求める方法はこちらの記事を参考にしてください。

エネルギーを用いる方法
今回紹介する方法は、システムのエネルギーを用いて運動方程式を算出します。
システムのエネルギーには、
- 運動エネルギー(Kinetic Energy: KE)
- 位置エネルギー(Potential Energy: PE)
があります。
このエネルギーから
$$ L = KE – PE $$
とした時、この\(L\)をラグランジアン(Lagrangian)と言います。
このラグランジアン\(L\)を用いて、ラグランジュ方程式(Lagrangian Equation)を作成することができます。
$$ \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{x}(t)} \right) – \frac{\partial L}{\partial x(t)} = 0 $$
この式にラグランジアン\(L\)を代入すると、
$$ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}(t)} \left( KE – PE \right) \right) – \frac{\partial}{\partial x(t)} \left( KE – PE \right) = 0 $$
となります。
ここで、
- 運動エネルギー\(KE\)は時間\(t\)と速度\(\dot{x}(t)\)の関数で、
- 位置エネルギー\(PE\)は時間\(t\)と速度\(x(t)\)の関数
だとすると、
$$ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}(t)} \left( KE(\dot{x}(t),t) – PE(x(t),t) \right) \right) – \frac{\partial}{\partial x(t)} \left( KE(\dot{x}(t),t) – PE(x(t),t) \right) = 0 $$
$$ \Rightarrow \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}(t)} KE(\dot{x}(t),t) \right) + \frac{\partial}{\partial x(t)} PE(x(t),t) = 0$$
とすることが出来ます。
この関係式を用いて運動方程式を求めていきます。
質量-ばねシステムの場合
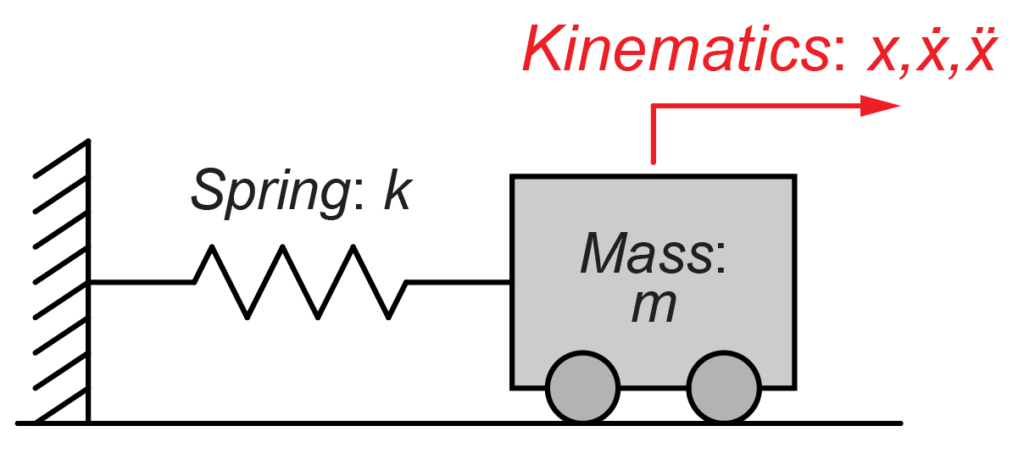
この質量-ばねシステムを例に運動方程式を求めていきます。
質量\(m\)とその速度\(\dot{x}(t)\)による運動エネルギー\(KE\)は、
$$ KE = \frac{1}{2} m \dot{x}^2 $$
となります。
ばね\(k\)による位置エネルギー\(PE\)は、
$$ PE = \frac{1}{2} k x^2 $$
となります。
これらのエネルギーを先ほどの関係式に代入すると、
$$ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}} \left( \frac{1}{2} m \dot{x}^2 \right) \right) + \frac{\partial}{\partial x} \left( \frac{1}{2} k x^2 \right) = 0$$
となります。
この式を解くと、
$$ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}} \left( \frac{1}{2} m \dot{x}^2 \right) \right) + \frac{\partial}{\partial x} \left( \frac{1}{2} k x^2 \right) = 0 $$
$$ \Rightarrow \frac{d}{dt} \left( m \dot{x} \right) + k x = 0 $$
$$ \Rightarrow m \ddot{x} + k x = 0 $$
となります。
ラグランジュ方程式を用いてシステムのエネルギーから運動方程式を求めることが出来ました。
ニュ―トンの運動の法則との比較
このシステムをニュートンの運動の法則を用いて運動方程式を求めると、
$$ m \ddot{x}(t) + k x(t) = 0 $$
となります。
詳しくはこちらの記事を参考にしてください。
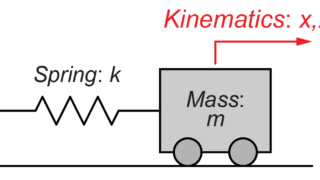
これより、今回紹介した方法で求めた運動方程式は、ニュートンの法則を用いて求めたものと同じになると分かりました。
まとめ
今回は、システムのエネルギーからラグランジュ方程式を用いて運動方程式を求める方法を紹介しました。
次回は今回紹介した方法を用いて実際にシステムの運動を求めていきたいと思います。























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
