実際に入力あり質量-ばね-ダンパーモデルの運動を計算する

今回は、実際に質量-ばね-ダンパーシステムを用いて、入力として力が質量にかかっている場合のシステムの運動を計算していきたいと思います。

入力あり質量-ばね-ダンパーシステムについての詳細は、こちらの記事を参考にしてください。

入力ありの質量-ばね-ダンパーモデルの運動を求める 今回は、質量-ばね-ダンパーモデルを用いて、入力として力が質量に与えられている場合のシステムの運動を考えます。 入...

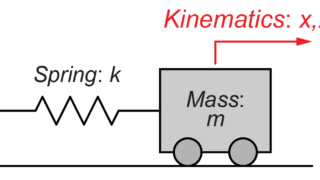
入力あり質量-ばね-ダンパーシステム

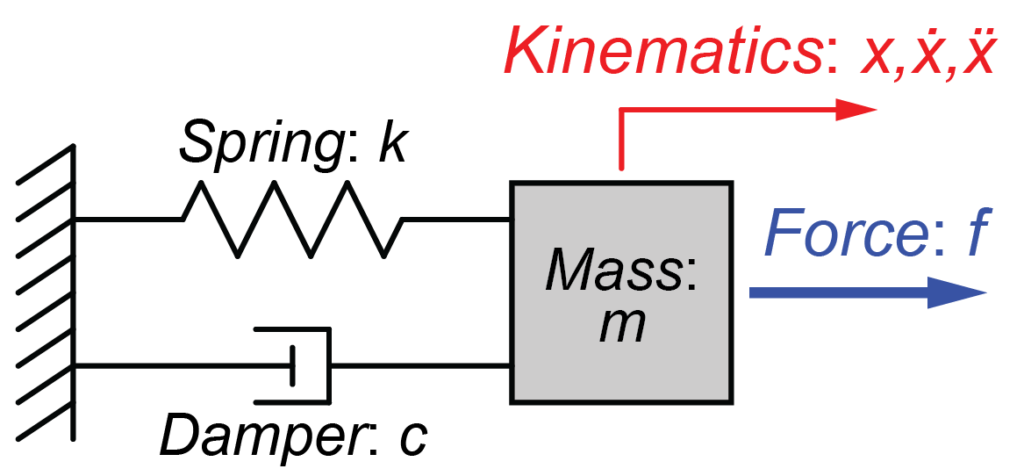
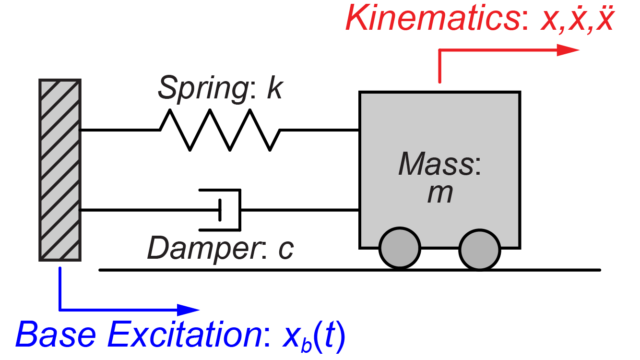
今回はこちらの入力あり質量-ばね-ダンパーモデルを用いて、システムの運動を求めていきます。

各パラメータの値は、質量\(m=5[kg]\)、ダンパー\(c=10[\frac{N}{m/s}kg]\)、ばね\(k=100[\frac{N}{m}]\)とします。

このシステムについて、力\(f(t)\)が

$$ f(t) = F_0 \sin \left( \omega t \right) = 10 \sin \left( 5 t \right) $$

と入力された場合のシステムの運動を計算していきます。

実際に具体例を用いて計算することで、システムの運動の様子が理解しやすくなると思います。

システムの運動方程式を解く

このシステムの運動方程式をニュートンの運動の法則

$$ \Sigma F = m a $$

を用いて求めます。

質量\(m\)にかかる力\(F\)の合計は、

$$ F = f(t) – c \dot{x}(t) – k x(t) $$

と表すことが出来るため、このシステムの運動方程式は加速度\(a=\ddot{x}(t)\)を用いて、

$$ m \ddot{x}(t) + c \dot{x}(t) + k x(t) = F_0 \sin \left( \omega t \right) $$

となります。

今回のパラメータをこの運動方程式に代入し、変位\(x(t)\)について解くことで、システムの運動を求めます。

システムの運動を求める

力あり質量-ばね-ダンパーシステムの運動方程式について、変位\(x(t)\)についての一般解は、

$$ x(t) = \underbrace{ e^{-\frac{c}{2 m}t} \left( C_1 \cos \left( \omega_d t \right) + C_2 \sin \left( \omega_d t \right) \right) }_{Transient Response} + \underbrace{ K_1 \sin \left( \omega t \right) + K_2 \cos \left( \omega t \right) }_{Steady State Response}$$

と表すことが出来ます。

過度応答（Transient Response）

過度応答\(x(t)\)とその速度\(\dot{x}(t)\)は

$$ x(t) = K_1 \sin \left( \omega t \right) + K_2 \cos \left( \omega t \right) $$

$$ \dot{x}(t) = K_1 \omega \cos \left( \omega t \right) – K_2 \omega \sin \left( \omega t \right) $$

と表されます。

この2式より、\(C_1\)と\(C_2\)を求めていきます。

時刻\(t\)で変位\(x(t)=0\)なので、

$$ x(0) = K_1 \sin \left( \omega \cdot 0 \right) + K_2 \cos \left( \omega \cdot 0 \right) = 0 $$

$$ \Rightarrow K_2 = 0 $$

となります。

時刻\(t\)で速度\(\dot{x}(t)=0\)なので、

$$ \dot{x}(0) = K_1 \omega \cos \left( \omega \cdot 0 \right) – K_2 \omega \sin \left( \omega \cdot 0 \right) = 0 $$

$$ \Rightarrow K_1 = 0 $$

となります。

これより、過度応答\(x(t)\)は、

$$ x(t) = 0 $$

となります。

この結果からも分かりますが、今回の例では初期条件による過度応答は無視できるので、
定常応答のみを考慮していきます。

定常応答

定常応答\(x(t)\)とその速度\(\dot{x}(t)\)と加速度\(\ddot{x}(t)\)は

$$ x(t) = K_1 \sin \left( \omega t \right) + K_2 \cos \left( \omega t \right) $$

$$ \dot{x}(t) = K_1 \omega \cos \left( \omega t \right) – K_2 \omega \sin \left( \omega t \right) $$

$$ \ddot{x}(t) = – K_1 \omega^2 \sin \left( \omega t \right) – K_2 \omega^2 \cos \left( \omega t \right) $$

と表されます。

この3式を運動方程式に代入し、\(K_1\)と\(K_2\)を求めていきます。

\(K_1\)と\(K_2\)について解くと、

$$ K_1 = F_0 \frac{k – m \omega^2}{\left( k – m \omega^2 \right)^2 + \left( c \omega \right)^2} = -0.08 $$

$$ K_2 = F_0 \frac{- c \omega}{\left( k – m \omega^2 \right)^2 + \left( c \omega \right)^2} = -0.16 $$

となります。

これより、このシステムの定常応答\(x(t)\)は、

$$ x(t) = -0.08 \sin \left( 5 t \right) -0.16 \cos \left( 5 t \right) $$

と表すことが出来ます。

横軸を時間\(t\)、縦軸を変位\(x\)としてグラフにすると下の図のようになります。

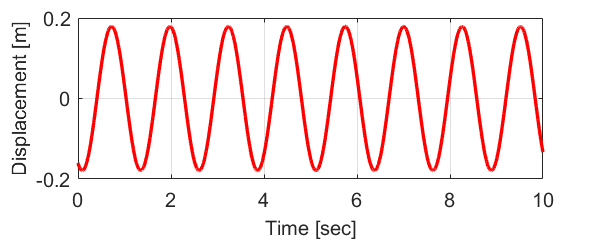
まとめ

今回は、入力ありの質量-ばね-ダンパーシステムについて、実際の例を用いてシステムの運動を算出する方法を紹介しました。

今回のシステムでは入力\(f(t)\)に応じて、システムが運動（振動）することが分かりました。