フーリエ変換を用いることで、時間による関数で与えられている信号に含まれる周波数成分を求めることが出来ます。
このフーリエ変換を行うためのプログラムは多く存在しますが、より理解を深めるために自分でプログラムを作ってみることにしました。
今回の記事では、実際にフーリエ変換を行うプログラムを作成し、動作を確認していきたいと思います。
フーリエ変換とは
フーリエ変換とは、時間t[sec]で与えられた関数f(t)を角周波数ω[rad/sec](または周波数f[Hz])の関数F(ω)に変換する手法のことを言います。
フーリエ変換の基本式
このフーリエ変換の基本式は
$$ F(\omega) = \int_{-\infty}^{\infty} f(x) e^{- i \omega x} dx $$
で与えられます。
このフーリエ変換の基本式は、角周波数ωの代わりに周波数kを用いて
$$ F(k) = \int_{-\infty}^{\infty} f(x) e^{-2\pi i k x} dx $$
と表すこともできます。
個人的には、周波数の方が角周波数より扱いやすいので、今回の記事では2つ目の式を用いていきたいと思います。
離散フーリエ変換
実際に取り扱う信号は、連続的な信号ではなく、一定間隔でサンプリングされた離散的な信号の場合が多いです。
この様な離散信号のフーリエ変換を行う方法として、離散フーリエ変換があります。
この離散フーリエ変換の基本式は、
$$ F(k) = \frac{1}{N} \displaystyle \sum_{ n = 0 }^{ N-1 } f(n) {W_N}^{kn} $$
で表されます。
ここで、基本式に含まれるWNは
$$ W_N = e^{-j \frac{2\pi}{N}} $$
で与えられます。
この任意の離散フーリエ変換の式を基に、与えられた離散信号に含まれる任意の周波数成分を求める式は
$$ F(\omega) = \frac{1}{N} \displaystyle \sum_{ n = 0 }^{ N-1 } f(n) e^{-j \omega T_s n} $$
となります。
フーリエ変換のプログラム
実際にMATLABで作成した離散フーリエ変換のプログラムについて説明します。
プログラム
離散フーリエ変換を行う関数:dft
function [Xk] = dft(xn,k,Ts) N = length(xn); for i = 1:length(k) Xk(i) = sum(xn.*exp(-1j*2*pi*k(i)*Ts.*(0:N-1)))/N; end end
解説
関数dft()に与える入力は、
- xn:変換したい離散信号
- k:求めたい周波数ベクトル
- Ts:離散信号のサンプリング間隔
です。
これらの値を入力として与えると、関数dft()内で
$$ F(\omega) = \frac{1}{N} \displaystyle \sum_{ n = 0 }^{ N-1 } f(n) e^{-j \omega T_s n} $$
の式を基に計算を行い
- Xk:離散フーリエ変換後の値
を出力します。
動作確認
動作確認のために
$$ x(t) = 2 \sin \left( 8 \pi t\right) + 3 \sin \left( 34 \pi t\right) $$
という信号を入力として与えた結果を下図に示します。
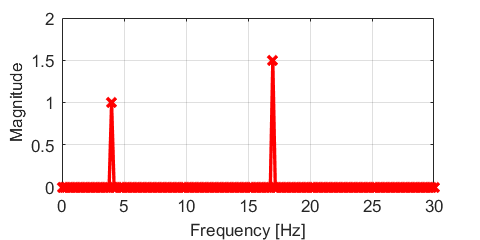
グラフをみると、4Hzと17Hzの周波数成分にピークが出ていることが分かります。
この離散フーリエ変換の結果より、入力信号には4Hzと17Hzの成分で構成されていることが分かりました。
実際に入力した離散信号の式は
$$ \begin{eqnarray} x(t) &=& 2 \sin \left( 8 \pi t\right) + 3 \sin \left( 34 \pi t\right) \\ &=& 2 \sin \left( 2 \pi 4 t\right) + 3 \sin \left( 2 \pi 17 t\right) \end{eqnarray}$$
のように4Hzと17Hzのsin波の足し合わせなので、この結果は正しいことが分かります。
絶対値が2分の1(半分)になっているのは、フーリエ変換の特性のためです。
※また機会(要望)があれば、詳しく説明したいと思います。
まとめ
今回は、フーリエ変換についての簡単な説明と、実際に作成したプログラムを紹介しました。
























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+

すみません、教えてください。
xnには右のワークスペースにてセルに
x(t)=2sin(8πt)+3sin(34πt)
の数値を作成しました。
その上でmatlabで実行すると
>> dft(xn,17,1)
左辺のインデックスが右辺とサイズが適合しないため、代入は実行できません。
エラー: dft (line 5)
Xk(i) = sum(xn.*exp(-1j*2*pi*k(i)*Ts.*(0:N-1)))/N;
と出てしまいますが、何か間違っている所あるでしょうか?
お教えください。よろしくお願い致します。
コメントありがとうございます。
x(t)を作成するためのtはどのように定義していますか?
また、その際のサンプリング時間Tsはどれくらいでしょうか?
dft(xn,17,1)と入力した場合、この入力信号xnのサンプリング時間Tsは1秒という事になります。
17Hzの信号の1周期は1/17で約58.8msです。
少なくともサンプリング時間は、この周期時間の半分よりも短くないとダメで、上手くフーリエ変換が出来ないです。
なので、入力信号のx(t)を作る際の時間tのサンプリング時間Tsを10msや1msにして試してみてください。
参考になれば幸いです。
すみません、色々としていたらxnの数値が転置していない事に気付き動きました。
このHPですと、4Hzと17Hzでもっとも大きな数字がピークが出るとのことですが
17Hzの計算結果は
> dft(xn,17,1)
このような記述でいいのでしょうか?
ちなみに、xnの元データは、1°ずつの数値を入力してありますので
0 2.8438 3.7212 2.2382 -0.1234
と入っております。
ご教授願います。よろしくお願い致します。
重ねてのご質問、ありがとうございます。
先に頂いたご質問の情報も併せて、実行プログラムを作成してみました。
Ts = 0.001;
t = 0:Ts:5-Ts;
xn = 2*sin(8*pi*t)+3*sin(34*pi*t);
dft(xn,17,Ts)
サンプリング時間Tsを1ms(0.001秒)として、5秒間の時間tを作成します。
そして時間tを用いて、入力信号xnを作成しています。
そして、入力信号xnと求めたい周波数17Hz、そしてサンプリング時間Tsを入力として関数dftを実行します。
このプログラムを実行することで、17Hzにおけるフーリエ変換の結果が得られると思います。
参考になれば幸いです。今後ともよろしくお願いいたします。
tajima さま
返信ありがとうございます。遅くなってしまいすみません。
実行プログラムの提示、ありがとうございます。
無事、結果を取得することが出来ました。
今現在、とある波形のフーリエ変換のプログラムを他言語で作っている
最中でして参考にさせて頂きたくいろいろとコメントさせて頂いた次第です。
その中でまだいくつか、分からないところや計算内容などがよく理解
できて居ない状況です。
もう少し疑問点を整理しますので、まとまり次第いくつか質問させて
頂きたいのですがよろしいでしょうか?
可能でしたらすみませんが、その時はよろしくお願い致します。
はじめまして
フーリエ変換について勉強中の学生です。現在、電圧波形V(t)を区分求積法にてフーリエ変換するプログラムを作成しているのですが、Tajima様の計算結果と同様に、出力波形の絶対値が元の波形の半分になりました。そこに疑問を持ち調べていたところ、ここにたどり着いた次第です。
>絶対値が2分の1(半分)になっているのは、フーリエ変換の特性のためです。
という一文が非常に気になります。ぜひ教えていただけないでしょうか。
よろしくお願いいたします。
コメント、ご質問ありがとうございます。
絶対値が2分の1(半分)になる理由には、ナイキスト周波数が影響しています。
ナイキスト周波数とは、サンプリングした値から信号を正しく復元できる最大の周波数のことで、サンプリング周波数の半分の周波数です。
例えば、サンプリング時間が1msの場合、サンプリング周波数は1kHzとなるため、ナイキスト周波数は500Hzとなります。
フーリエ変換では、サンプリング時間が1msの場合、出力結果は1kHzまで出力されます。
しかし、実際に入力信号をフーリエ変換した結果は、このナイキスト周波数500Hzを基準に対称(折りたたんだら重なる感じ)になります。
つまり、10Hzの入力信号をフーリエ変換した場合は、10Hzと990Hzにピークが出ます。
また、150Hzの入力信号の場合は、150Hzと850Hzにピークが出現します。
これは、500Hz以上は正しく復元できていないため生じる現象です。
そのため通常は、ナイキスト周波数以上の値は使用しません。
しかし、フーリエ変換の結果としては2つのピークで1つの入力信号を表しています。
例えば、10Hzと990Hzの2つのピークで10Hzを表します。
そのため、ナイキスト周波数以上の周波数成分990Hzを除いた場合、対象の入力信号の周波数成分10Hzに対する出力値は半分となります。
文字のみで長々となりましたが、参考になれば幸いです。
今度また図を用いて記事にまとめたいと思います。
ご返信ありがとうございます。遅くなり申し訳ありません。
tajima様のおかげで疑問を解消することができました。大変参考になるご回答を頂けて嬉しく思います。今回教えて頂いたことをプログラムに反映できるよう、書き直してみたいと思います。
ご教授いただきありがとうございました。