2リンクモデルのヤコビ行列を算出する方法

ヤコビ行列を用いることで、ロボットの「関節の速度」と「手先の速度」の関係を示すことが出来ます。

ヤコビ行列を使ってロボットの運動を計算する今回はヤコビ行列について説明したいと思います。ヤコビ行列を使うことで、ロボットの「関節の速度」と「手先の速度」の...

しかし、ヤコビ行列の算出式には偏微分が含まれていることで、一見すると難しく感じてしまう方も多くいます。

今回の記事では、2リンクモデルのヤコビ行列を算出する方法について説明したいと思います。

Contents

2リンクモデルと順運動学
2リンクモデルのヤコビ行列
- ヤコビ行列
- ヤコビ行列の算出
まとめ

2リンクモデルと順運動学

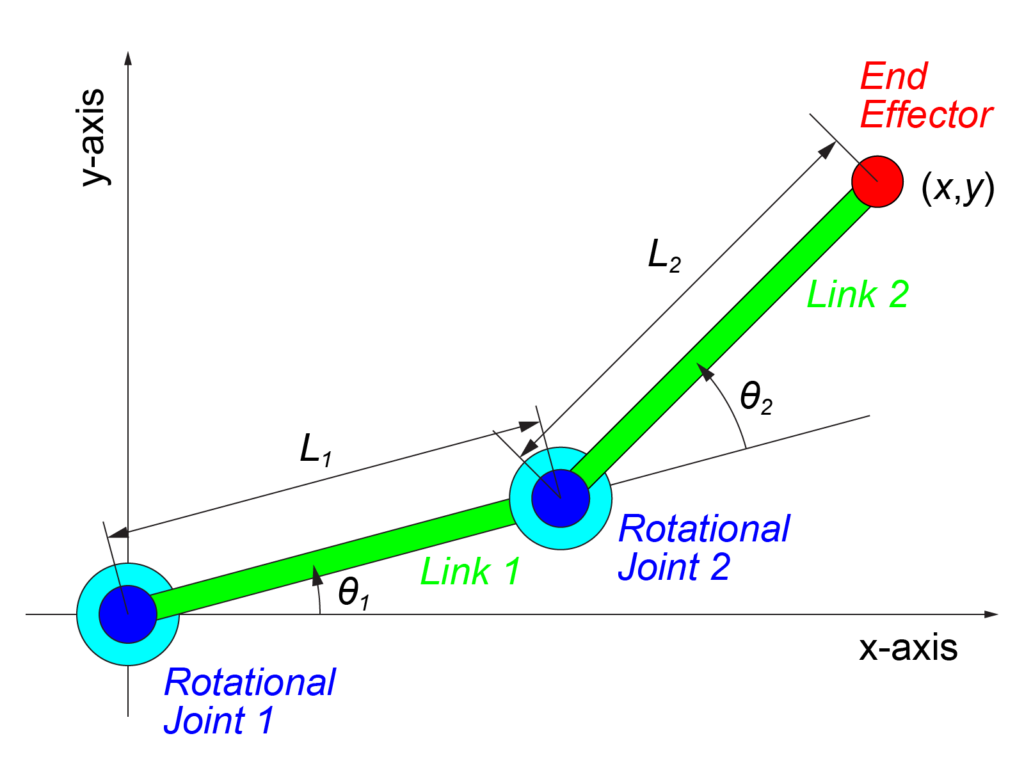
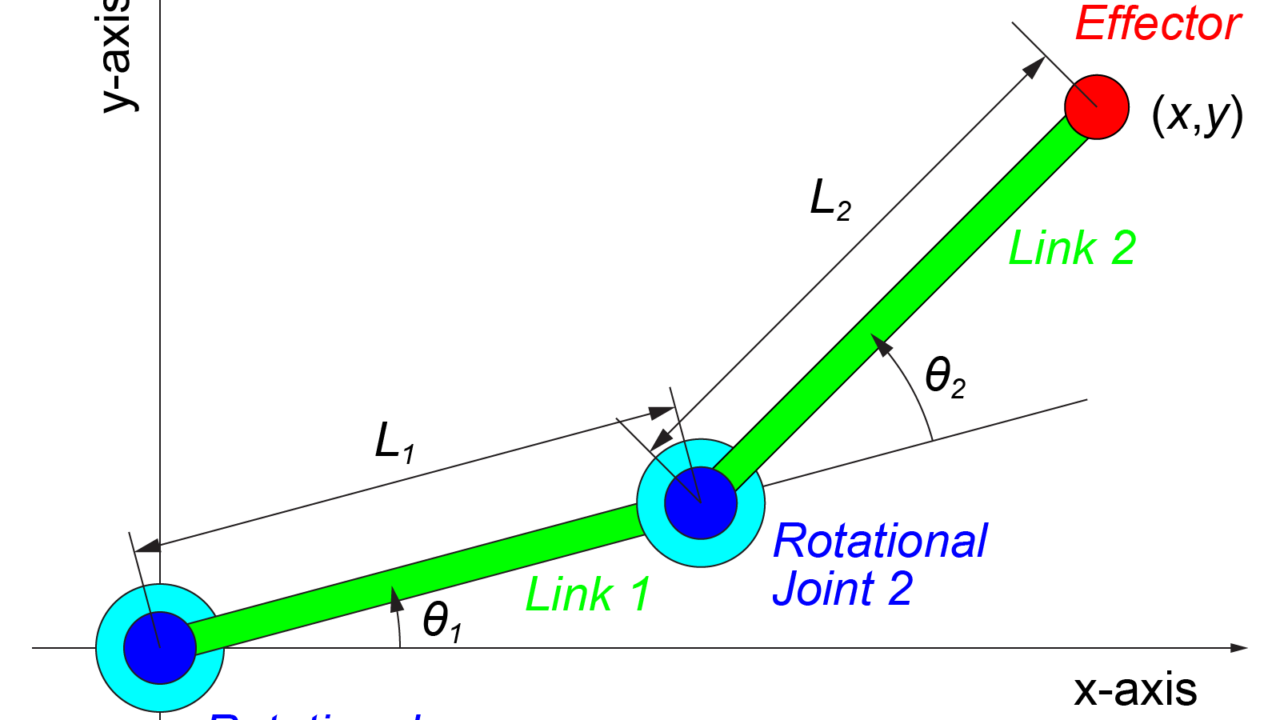
今回の記事で取り扱う2リンクモデルについて、「関節の変位（θ₁、θ₂）」から「ロボットの位置（x、y）」を求めるための順運動学の式は

$$ \begin{eqnarray} \left\{ \begin{array}{l} x &=& L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) \\ y &=& L_1 \sin \left( \theta_1 \right) + L_2 \sin \left( \theta_1 + \theta_2 \right) \end{array} \right. \end{eqnarray} $$

で表されます。

この順運動学の式について、それぞれの式を各変数で偏微分することで、ヤコビ行列を算出していきます。

順運動学の算出方法の詳細は、こちらの記事を参考にしてください。

２リンクモデルの運動学を求めてみよう！簡単に順運動学の式を算出する方法ロボット工学を学び、ロボットや機械を制御する際に、順運動学や逆運動学を理解することはとても重要です。以前の記事で...

2リンクモデルのヤコビ行列

算出した2リンクモデルの順運動学から、ヤコビ行列を求める流れを紹介します。

ヤコビ行列

ヤコビ行列は、順運動学の各式を各変数で偏微分したものを行列の形で表すことで求められます。

例えば、順運動学の式が2つ（f₁とf₂）で変数も2つ（x₁とx₂）ある場合について、ヤコビ行列の基本式は

$$ \boldsymbol{ J } = \begin{bmatrix} \frac{ \partial f_1 }{ \partial x_1 } & \frac{ \partial f_1 }{ \partial x_2 } \\ \frac{ \partial f_2 }{ \partial x_1 } & \frac{ \partial f_2 }{ \partial x_2 } \end{bmatrix} $$

のように表されます。

今回の2リンクモデルのケースでは、順運動学の式には「ロボットの位置（x、y）」の2式と「関節の変位（θ₁、θ₂）」の2変数があります。

よって、2リンクモデルのヤコビ行列は

$$ \boldsymbol{ J } = \begin{bmatrix} \frac{ \partial x }{ \partial \theta_1 } & \frac{ \partial x }{ \partial \theta_2 } \\ \frac{ \partial y }{ \partial \theta_1 } & \frac{ \partial y }{ \partial \theta_2 } \end{bmatrix} $$

を算出することで求めることが出来ます。

ヤコビ行列の算出

では、実際に2リンクモデルについて順運動学の式からヤコビ行列を求めていきたいと思います。

まず初めに、ロボットのx軸についての偏微分を考えます。

x軸の位置についての順運動学の式について、根元の関節の変位θ₁について偏微分すると

$$ \begin{eqnarray} \frac{ \partial x }{ \partial \theta_1 } &=& \frac{ \partial }{ \partial \theta_1 } \left\{ L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) \right\} \\ &=& – L_1 \sin \left( \theta_1 \right) – L_2 \sin \left( \theta_1 + \theta_2 \right) \end{eqnarray} $$

となります。

そして、2つ目の関節の変位θ₂について偏微分を行うと

$$ \begin{eqnarray} \frac{ \partial x }{ \partial \theta_2 } &=& \frac{ \partial }{ \partial \theta_2 } \left\{ L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) \right\} \\ &=& – L_2 \sin \left( \theta_1 + \theta_2 \right) \end{eqnarray} $$

と求めることが出来ます。

同様に、y軸ついての順運動学の式に対して、各関節の変位θ₁とθ₂について偏微分を行うと

$$ \begin{eqnarray} \frac{ \partial y }{ \partial \theta_1 } &=& \frac{ \partial }{ \partial \theta_1 } \left\{ L_1 \sin \left( \theta_1 \right) + L_2 \sin \left( \theta_1 + \theta_2 \right) \right\} \\ &=& L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) \\ \frac{ \partial y }{ \partial \theta_2 } &=& \frac{ \partial }{ \partial \theta_2 } \left\{ L_1 \sin \left( \theta_1 \right) + L_2 \sin \left( \theta_1 + \theta_2 \right) \right\} \\ &=& L_2 \cos \left( \theta_1 + \theta_2 \right) \end{eqnarray} $$

のように表すことが出来ます。

これより、2リンクモデルのヤコビ行列は求めた偏微分の式を代入して

$$ \begin{eqnarray} \boldsymbol{ J } &=& \begin{bmatrix} \frac{ \partial x }{ \partial \theta_1 } & \frac{ \partial x }{ \partial \theta_2 } \\ \frac{ \partial y }{ \partial \theta_1 } & \frac{ \partial y }{ \partial \theta_2 } \end{bmatrix} \\ &=& \begin{bmatrix} – L_1 \sin \left( \theta_1 \right) – L_2 \sin \left( \theta_1 + \theta_2 \right) & – L_2 \sin \left( \theta_1 + \theta_2 \right) \\ L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) & L_2 \cos \left( \theta_1 + \theta_2 \right) \end{bmatrix} \end{eqnarray}$$

と算出することが出来ました。