今回のシリーズでは、ロボットや自動運転車を制御する際にとても重要となる、ロボットや車の正確な位置を知る方法として、カルマンフィルタを用いたロボットの位置推定の方法を紹介しています。
前回の記事では、本シリーズで取り扱うカルマンフィルタを用いた自己位置推定の問題と線形動的システムについて説明しました。

今回は、この雑音が含まれている線形動的システムの自己位置推定問題を解くために、カルマンフィルタの基本的な式を紹介していきたいと思います。
取り扱う問題とシステム
前回の記事で紹介した本シリーズで取り扱うカルマンフィルタによるロボットの位置推定問題と線形動的システムについておさらいします。
自己位置推定問題
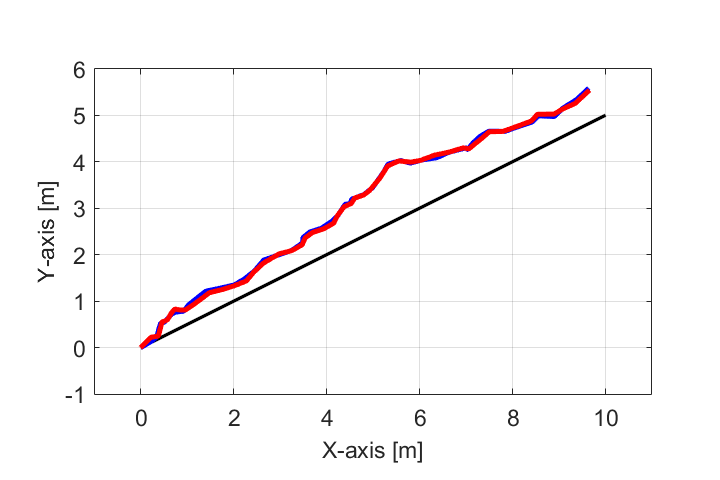
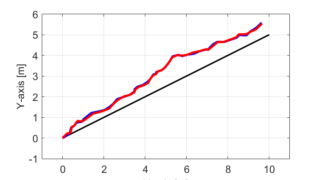
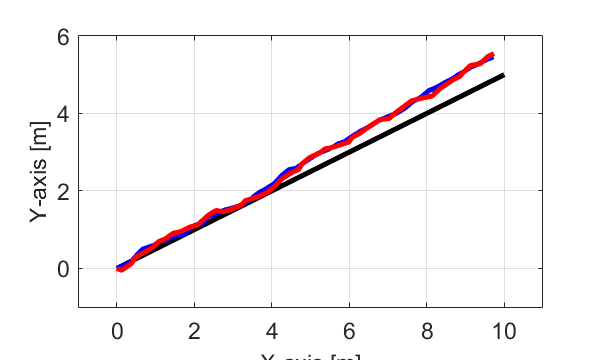
本シリーズでは、上の図で表されるように黒線の目標軌跡から青線のように実際の軌跡がずれた場合について、カルマンフィルタを用いて赤線のようにロボットの位置を推定する問題を考えています。
線形動的システム
本シリーズで取り扱う線形動的システムの状態空間モデルは
$$ \begin{eqnarray} \boldsymbol{x}_t &=& \boldsymbol{F}_t \boldsymbol{x}_{t-1} + \boldsymbol{B}_t \boldsymbol{u}_t + \boldsymbol{w}_t \\ \boldsymbol{z}_t &=& \boldsymbol{H}_t \boldsymbol{x}_{t} + \boldsymbol{v}_t \end{eqnarray} $$
のように、入力や観測に雑音(wやv)が含まれているモデルを考えます。
このように、状態方程式に雑音wが含まれていることから目標軌跡に対して実際の軌跡にズレが生じます。
また、出力方程式にも雑音vが含まれているため、正確なロボットの位置を得ることもできません。
このようなロボットの自己位置を推定する問題についてカルマンフィルタを用いた解法を考えていきます。
カルマンフィルタの基本式
カルマンフィルタを適用した位置推定を行うために、カルマンフィルタの基本的な式を紹介していきます。
カルマンフィルタを行う際の定義として、時刻tでのロボットの推定状態を\(\hat{\boldsymbol{x}}_{t|t}\)と置きます。
また、時刻tでの予測の不確かさを示す誤差共分散を\(\hat{\boldsymbol{P}}_{t|t}\)で表す事とします。
カルマンフィルタには大きく
- 予測ステップ
- 更新ステップ
の2つのステップがあります。
この2つのステップについて、基本式とその役割を紹介していきます。
予測ステップ
予測ステップは、1つ前の状態を用いて現在の状態を予測するステップです。
つまり、時刻t-1での推定状態\(\hat{\boldsymbol{x}}_{t-1|t-1}\)と誤差共分散\(\hat{\boldsymbol{P}}_{t-1|t-1}\)を用いて、時刻tでの推定状態と誤差共分散を予測していきます。
推定状態の予測
時刻t-1の推定状態\(\hat{\boldsymbol{x}}_{t-1|t-1}\)から予測した時刻tでのロボットの推定状態を\(\hat{\boldsymbol{x}}_{t|t-1}\)とします。
この推定状態\(\hat{\boldsymbol{x}}_{t|t-1}\)の算出は状態方程式を用いて表すと
$$ \hat{\boldsymbol{x}}_{t|t-1} = \boldsymbol{F}_t \hat{\boldsymbol{x}}_{t-1|t-1} + \boldsymbol{B}_t \boldsymbol{u}_t $$
となり、時刻t-1でのロボットの推定状態\(\hat{\boldsymbol{x}}_{t-1|t-1}\)から予測することが出来ます。
上の式からも分かるように、この時は先の線形動的システムの状態方程式で考慮していた雑音wtによる影響を含んでいません。
これは、未来に起こる雑音による誤差を実際に求めることは不可能なので、推定状態を予測する際はこの誤差を含めずに算出しています。
この雑音wtを除くことによる影響は、誤差共分散\(\hat{\boldsymbol{P}}\)を求める際に考慮します。
誤差共分散の予測
時刻tでの誤差共分散\(\hat{\boldsymbol{P}}_{t|t}\)を時刻t-1の状態から予測した誤差共分散\(\hat{\boldsymbol{P}}_{t|t-1}\)を求めていきます。
この誤差共分散\(\hat{\boldsymbol{P}}_{t|t-1}\)は
$$ \hat{\boldsymbol{P}}_{t|t-1} = \boldsymbol{F}_t \hat{\boldsymbol{P}}_{t-1|t-1} {\boldsymbol{F}_t}^T + \boldsymbol{Q}_t $$
のように、時刻t-1での誤差共分散\(\hat{\boldsymbol{P}}_{t-1|t-1}\)を用いて予測をしていきます。
ここで、この誤差共分散\(\hat{\boldsymbol{P}}_{t|t-1}\)は、推定状態の不確かさを表しています。
そして、推定状態を予測する際に雑音による影響を無視していることから、推定状態の不確かさが増大し、この誤差共分散も雑音を示す共分散行列Qtの分だけ大きくなります。
小まとめ
この2つの式
$$ \begin{eqnarray} \left\{ \begin{array} \hat{\boldsymbol{x}}_{t|t-1} = \boldsymbol{F}_t \hat{\boldsymbol{x}}_{t-1|t-1} + \boldsymbol{B}_t \boldsymbol{u}_t \\ \hat{\boldsymbol{P}}_{t|t-1} = \boldsymbol{F}_t \hat{\boldsymbol{P}}_{t-1|t-1} {\boldsymbol{F}_t}^T + \boldsymbol{Q}_t \end{array} \right. \end{eqnarray} $$
がカルマンフィルタの予測ステップにおける基本式です。
更新ステップ
更新ステップでは、予測した状態と観測の情報を用いて現在の状態を更新するステップです。
つまり、時刻\(t-1\)での推定状態\(\hat{\boldsymbol{x}}_{t-1|t-1}\)と誤差共分散\(\hat{\boldsymbol{P}}_{t-1|t-1}\)から予測した推定状態\(\hat{\boldsymbol{x}}_{t|t-1}\)と誤差共分散\(\hat{\boldsymbol{P}}_{t|t-1}\)に加えて、観測による情報\(\boldsymbol{z}_t\)用いて、時刻\(t\)での推定状態\(\hat{\boldsymbol{x}}_{t|t}\)と誤差共分散\(\hat{\boldsymbol{P}}_{t|t}\)を更新していきます。
観測残差の算出
実際に観測により得た情報ztと予測した推定状態\(\hat{\boldsymbol{x}}_{t|t-1}\)で得られるであろう観測情報から観測残差\(\tilde{\boldsymbol{y}}_t\)
$$ \tilde{\boldsymbol{y}}_t = \boldsymbol{z}_t – \boldsymbol{H}_t \hat{\boldsymbol{x}}_{t|t-1} $$
を求めます。
この観測残差\(\tilde{\boldsymbol{y}}_t\)は、ロボットが実際にセンサから得た観測情報ztと、出力方程式
$$ \boldsymbol{z}_t = \boldsymbol{H}_t \boldsymbol{x}_{t} $$
を用いてロボットが予測した推定状態\(\hat{\boldsymbol{x}}_{t|t-1}\)に存在したとしたら得られるであろう観測情報との差を表しています。
このとき、従来の出力方程式に含まれている雑音vによる影響は考慮せずに観測残差\(\tilde{\boldsymbol{y}}_t\)を求めています。
観測残差の共分散を算出
観測残差\(\tilde{\boldsymbol{y}}_t\)を求める際に用いた出力方程式から取り除いた雑音vによる影響として観測残差の共分散Stを求めていきます。
観測残差の共分散Stは、出力方程式の誤差共分散Rtと予測した誤差共分散\(\hat{\boldsymbol{P}}_{t|t-1}\)を用いて
$$ \boldsymbol{S}_t = \boldsymbol{R}_t + \boldsymbol{H}_t \boldsymbol{P}_{t|t-1} {\boldsymbol{H}_t}^T $$
と算出することが出来ます。
カルマンゲインの最適化
これまでに予測した誤差共分散\(\boldsymbol{P}_{t|t-1}\)と求めた観測残差の共分散StからカルマンゲインKtは
$$ \boldsymbol{K}_t = \boldsymbol{P}_{t|t-1} {\boldsymbol{H}_t}^T {\boldsymbol{S}_t}^{-1} $$
と算出することが出来ます。
このカルマンゲインKtを用いて、時刻tでの推定状態\(\hat{\boldsymbol{x}}_{t|t}\)と誤差共分散\(\hat{\boldsymbol{P}}_{t|t}\)を求めていきます。
推定値の更新
算出したカルマンゲインKtを用いて、予測ステップで求めた推定状態\(\hat{\boldsymbol{x}}_{t|t-1}\)を更新します。
時刻tでの推定状態\(\hat{\boldsymbol{x}}_{t|t}\)は
$$ \hat{\boldsymbol{x}}_{t|t} = \hat{\boldsymbol{x}}_{t|t-1} + \boldsymbol{K}_t \tilde{\boldsymbol{y}}_t $$
のように、カルマンゲインKtと観測残差\(\tilde{\boldsymbol{y}}_t\)を用いて、予測ステップで求めた推定状態\(\hat{\boldsymbol{x}}_{t|t-1}\)を更新することで算出します。
誤差の共分散の更新
同様に、予測ステップで求めた誤差共分散\(\hat{\boldsymbol{P}}_{t|t-1}\)をカルマンゲインKtを用いて更新します。
時刻tでの誤差共分散\(\hat{\boldsymbol{P}}_{t|t}\)は
$$ \hat{\boldsymbol{P}}_{t|t} = \left( \boldsymbol{I} – \boldsymbol{K}_t \boldsymbol{H}_t \right) \boldsymbol{P}_{t|t-1} $$
とカルマンゲインKtを用いて、予測ステップで求めた誤差共分散\(\hat{\boldsymbol{P}}_{t|t-1}\)を更新することで算出します。
小まとめ
これら5つの式
$$ \begin{eqnarray} \left\{ \begin{array} \tilde{\boldsymbol{y}}_t = \boldsymbol{z}_t – \boldsymbol{H}_t \hat{\boldsymbol{x}}_{t|t-1} \\ \boldsymbol{S}_t = \boldsymbol{R}_t + \boldsymbol{H}_t \boldsymbol{P}_{t|t-1} {\boldsymbol{H}_t}^T \\ \boldsymbol{K}_t = \boldsymbol{P}_{t|t-1} {\boldsymbol{H}_t}^T {\boldsymbol{S}_t}^{-1} \\ \hat{\boldsymbol{x}}_{t|t} = \hat{\boldsymbol{x}}_{t|t-1} + \boldsymbol{K}_t \tilde{\boldsymbol{y}}_t \\ \hat{\boldsymbol{P}}_{t|t} = \left( \boldsymbol{I} – \boldsymbol{K}_t \boldsymbol{H}_t \right) \boldsymbol{P}_{t|t-1} \end{array} \right. \end{eqnarray} $$
がカルマンフィルタの更新ステップにおける基本式になります。
まとめ
今回は、入力や出力に雑音が含まれている線形動的システムについて、ロボットの自己位置推定を行うためにカルマンフィルタの基本的な式を紹介しました。
次回は、このカルマンフィルタの基本式を用いて実際にロボットの位置推定を行いたいと思います。

合わせて読みたい
カルマンフィルタを使った自己位置推定についてのまとめ記事はこちら



























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
