２リンクモデルの運動学を求めてみよう！簡単に順運動学の式を算出する方法

ロボット工学を学び、ロボットや機械を制御する際に、順運動学や逆運動学を理解することはとても重要です。

以前の記事では、順運動学と逆運動学についての基本知識と簡単なモデルでの各運動学の算出結果を紹介しました。

ロボット工学の基礎　順運動学と逆運動学を理解するロボット工学を学ぶうえで必要な基本、『順運動学』と『逆運動学』について解説してきます。運動学の定義運動学...

今回からの記事では、少し複雑な例として2リンクモデルにおける運動学（順運動学と逆運動学）を求める方法を紹介したいと思います。

Contents

順運動学と逆運動学とは
2リンクモデルとは
順運動学の算出
まとめ

順運動学と逆運動学とは

前回のおさらいです。

運動学とは、ロボットの『関節の角度や長さ』と『位置や姿勢』との関係を表した式です。

この運動学には、下記の通り順運動学と逆運動学の2つがあります。

まず順運動学とは、「関節の変位（角度や長さ）から、ロボットの位置や姿勢を求める方法」を言います。

そして逆運動学とは、「ロボットの位置や姿勢から、関節の変位（角度や長さ）を求める方法」です。

この対の関係になっている順運動学と逆運動学の式は、ロボットを望み通りに制御するためにとても重要です。

運動学（順運動学と逆運動学）についての詳細は、こちらの記事を参考にしてください。

2リンクモデルとは

今回は、2つのリンク（Link）がそれぞれ回転関節（Rotational Joint）で接続された2リンクモデルを用いて運動学の算出を求めます。

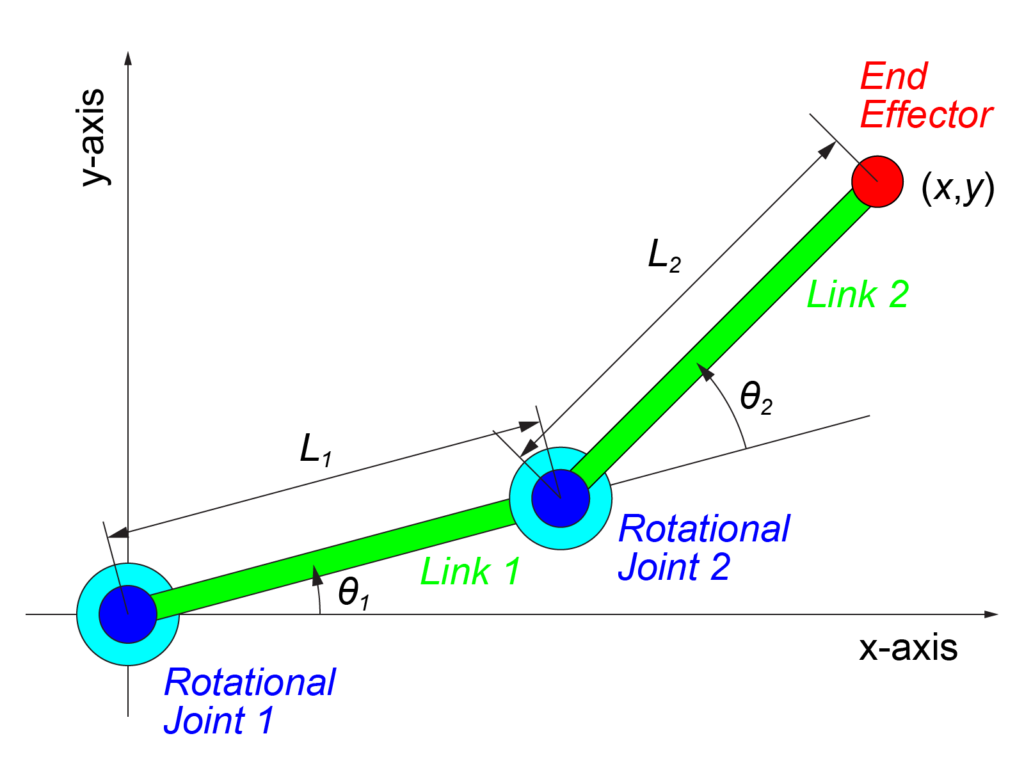
原点にある回転関節1にリンク1が接続され、そのリンク1の反対側に回転関節2とリンク2が接続されたモデルです。

今回取り扱うモデルについて、「関節の変位（角度や長さ）」は回転関節1と2の角度θ₁とθ₂で、「ロボットの位置や姿勢」はリンク2の手先の位置（End Effector）のxとyです。

また、各リンクの長さはそれぞれL₁とL₂として考えます。

この2リンクモデルについて、順運動学と逆運動学の式を求めていきます。

順運動学の算出

まず初めに、2リンクモデルの順運動学を求めていきます。

順運動学の式を求めるために、関節の変位である各関節角度θ₁とθ₂を用いて、ロボットの位置である手先の位置xとyを数式で表します。

リンク1について

まず原点にある回転関節1とリンク1より、原点からリンク1の先の回転関節2の位置x₁とy₁は

$$ \begin{eqnarray} \left\{ \begin{array}{l} x_1 &=& L_1 \cos \theta_1 \\ y_1 &=& L_1 \sin \theta_1 \end{array} \right. \end{eqnarray} $$

のように三角関数を用いて求められます。

リンク2について

つぎに、回転関節2を基準としたときのリンク2の先の位置を求めます。

リンク2の角度は、回転関節2に加えて回転関節1の角度も影響します。

よって、リンク2の角度θは

$$ \theta = \theta_1 + \theta_2 $$

のように、2つの回転関節の角度θ₁とθ₂を足し合わせた値となります。

これより、回転関節2の位置を基準とした時のリンク2の先の位置x₂とy₂は、

$$ \begin{eqnarray} \left\{ \begin{array}{l} x_2 &=& L_2 \cos \left( \theta_1 + \theta_2 \right) \\ y_2 &=& L_2 \sin \left( \theta_1 + \theta_2 \right) \end{array} \right. \end{eqnarray} $$

のように三角関数を用いて求められます。

モデル全体の式

最後に原点を基準としたロボットの手先の位置xとyを求めます。

ロボットの位置は、これまでに求めた2つのリンクや回転関節を用いて求めた距離の足し合わせで求められるため、

$$ \begin{eqnarray} \left\{ \begin{array}{l} x &=& x_1 + x_2 &=& L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) \\ y &=& y_1 + y_2 &=& L_1 \sin \left( \theta_1 \right) + L_2 \sin \left( \theta_1 + \theta_2 \right) \end{array} \right. \end{eqnarray} $$

となります。

よって、取り扱っている2リンクモデルの「関節の変位（θ₁、θ₂）」から「ロボットの位置（x、y）」を求めるための順運動学の式は

$$ \begin{eqnarray} \left\{ \begin{array}{l} x &=& L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) \\ y &=& L_1 \sin \left( \theta_1 \right) + L_2 \sin \left( \theta_1 + \theta_2 \right) \end{array} \right. \end{eqnarray} $$

で表されることが分かりました。