ロボットの軌跡生成：直線補間

軌跡生成（Trajectory Generation）とは、ロボットの状態（位置や姿勢）をある点から他の点に移動させるために、必要な各時間における位置および速度などの情報を作成することです。

今回は、1次元のx軸上でのみ動くロボットの直線補間（Linear Interpolation）について紹介します。

1次元の直線補間

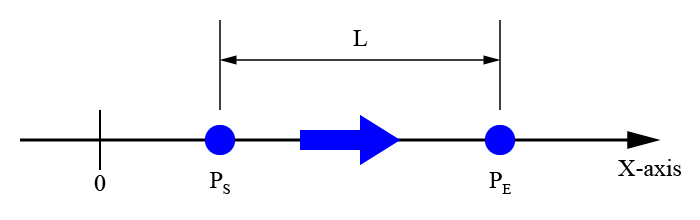※図を挿入

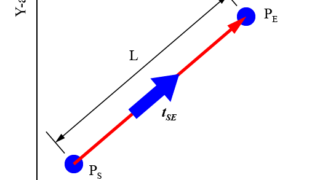
作成したいロボットの軌跡について、始点\(P_S\)を
$$ P_S = X_S $$
終点\(P_E\)を
$$ P_E = X_E $$
とします。

この2点を直線で補間する経路を求めていきます。

始点‐終点間の距離

ロボットが始点\(P_S\)から終点\(P_E\)まで直線で移動した場合の距離\(L\)を求めます。

1次元の座標軸上の2点間の距離\(L\)は、

$$ L = P_E – P_S = X_E – X_S $$

で求めることが出来ます。

ロボットの速度に対する移動時間

ロボットの速度が与えられた時に必要な時間を求めていきます。

2点間を移動するロボットの速度が早ければ、移動に必要な時間は短くなります。

反対に、ロボットの速度が遅ければ、その分移動に必要な時間が長くなります。

ロボットの速度を\(V[m/sec]\)とすると、ロボットが距離\(L[m]\)移動するために必要な時間\(T[sec]\)は、

$$ T = \frac{L}{V} $$

で求めることが出来ます。

移動時間に対するロボットの速度

ロボットに2点間の移動時間が与えられた時に必要な速度を求めていきます。

ロボットに与えられた移動時間が長ければ、必要なロボットの速度は遅くなります。

反対に移動時間が短ければロボットの速度を上げる必要があります。

ロボットに与えられた移動時間を\(T[sec]\)とすると、この時間内にロボットが距離\(L[m]\)移動するために必要な速度\(V[m/sec]\)は、

$$ V = \frac{L}{T} $$

で求めることが出来ます。

軌跡生成

求めた2点間の距離\(L\)、ロボットの速度\(V\)、移動時間\(T\)を基にして、ロボットの軌跡を生成出来ます。

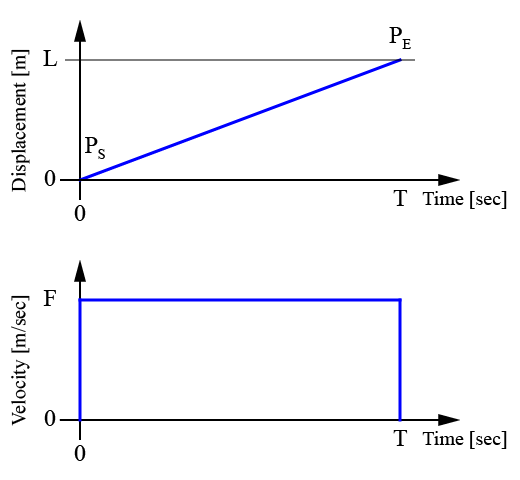
グラフのように求めたパラメータを用いることで、ロボットが2点間を結ぶ直線（距離\(L[m]\)）を等速（速度\(V[m/sec]\)）で移動（時間\(T[sec]\)）するために必要な軌跡を直線補間で求めることが出来ました。

まとめ

今回は1次元のx軸上のみを動くロボットを例に取り、2点間を線形補間した際のロボットの軌跡生成を行いました。

次回は、2次元のXY平面を移動するロボットについて、線形補間を用いて軌跡生成をする方法を紹介したいと思います。