可操作性楕円体を用いることで、ロボットの手先がどの方向にどれくらい動かしやすいかが分かります。
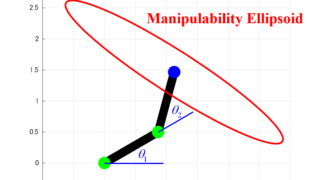
この可操作性楕円体は、システムのヤコビ行列を用いて算出することが出来ます。
今回からの記事では、2リンクモデルのロボットを用いて、実際にヤコビ行列から可操作性楕円体を求める方法を紹介します。
2リンクモデルとヤコビ行列
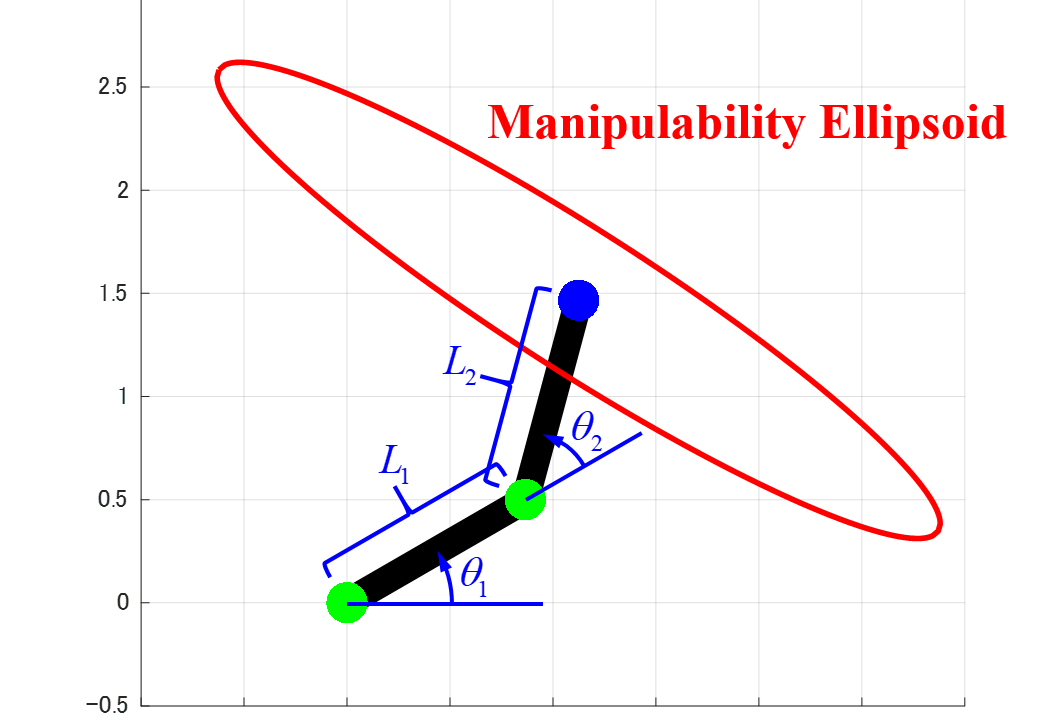
今回の記事では、下図のような2リンクモデルの可操作性楕円体を取り扱います。
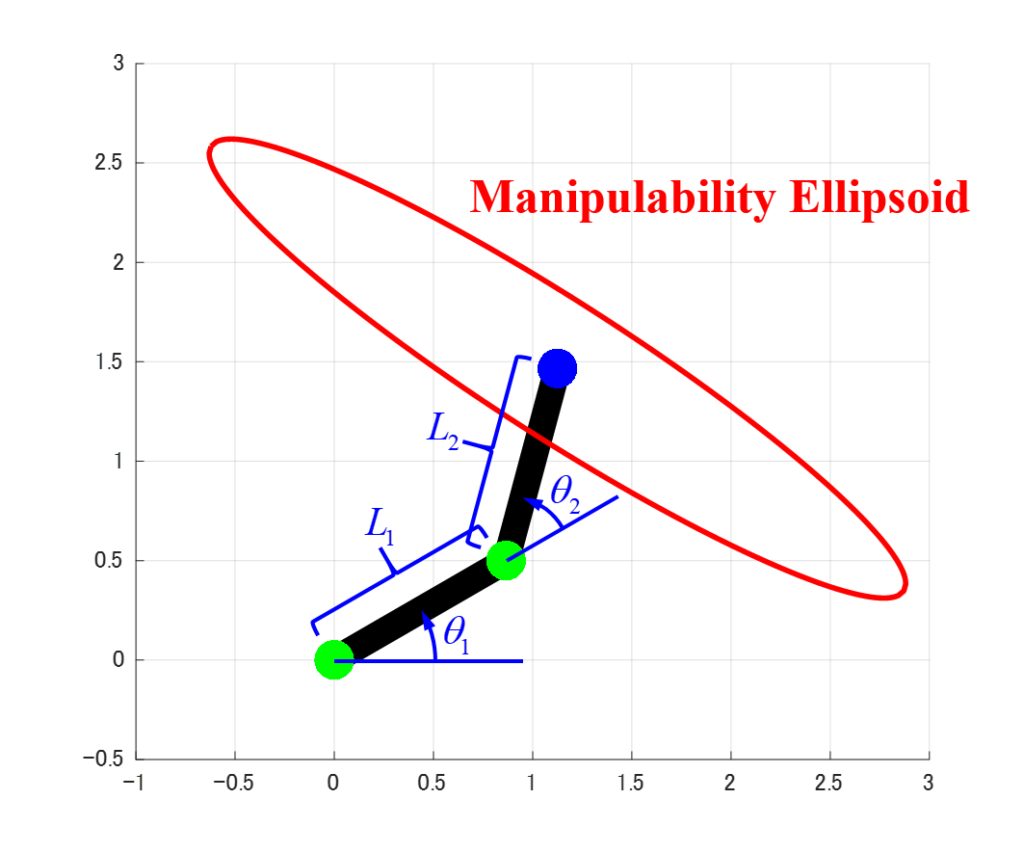
今回の記事で取り扱う2リンクモデルは、上図のように2つの回転関節により構成されたXY平面上で動作するロボットです。
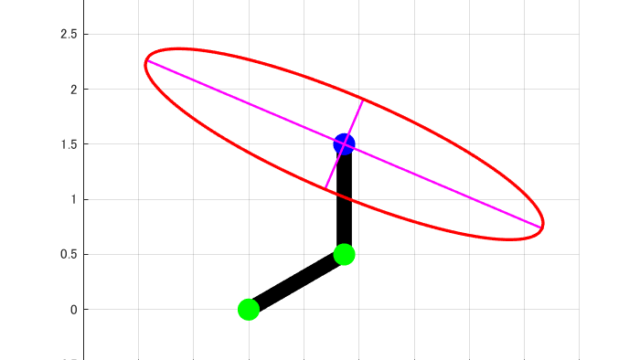
動作範囲がXY平面上のため、求める可操作性楕円体は平面の楕円形状になります。
この2リンクモデルの可操作性楕円体を求めるために必要となる、運動学の式とヤコビ行列について紹介します。
以前の記事でも紹介したため、既に分かっている人はおさらい程度に流してください。
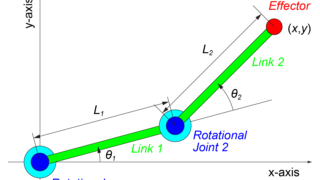

運動学
まず、取り扱う2リンクモデルについて、運動学を用いて関節状態θとロボット手先状態xの関係を求めます。
2リンクモデルの関節状態θ=[θ1, θ2]Tとロボット手先状態x=[x, y]Tの関係は
$$ \begin{eqnarray} \left\{ \begin{array}{l} x &=& L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) \\ y &=& L_1 \sin \left( \theta_1 \right) + L_2 \sin \left( \theta_1 + \theta_2 \right) \end{array} \right. \end{eqnarray} $$
と表されます。
詳しい算出方法については、こちらの記事を参考にしてください。

ヤコビ行列
運動学で得た関節状態θとロボット手先状態xの関係式からヤコビ行列Jを算出します。
ヤコビ行列とは、関節速度dθ/dtとロボット手先速度dx/dtの関係を表す行列で、
$$ \boldsymbol{\dot{x}} = \boldsymbol{J}(\theta) \boldsymbol{\dot{\theta}} $$
の関係を示します。
ヤコビ行列は、運動学の式を各関節状態について偏微分することで
$$ \begin{eqnarray} \boldsymbol{ J } &=& \begin{bmatrix} \frac{ \partial x }{ \partial \theta_1 } & \frac{ \partial x }{ \partial \theta_2 } \\ \frac{ \partial y }{ \partial \theta_1 } & \frac{ \partial y }{ \partial \theta_2 } \end{bmatrix} \\ &=& \begin{bmatrix} – L_1 \sin \left( \theta_1 \right) – L_2 \sin \left( \theta_1 + \theta_2 \right) & – L_2 \sin \left( \theta_1 + \theta_2 \right) \\ L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) & L_2 \cos \left( \theta_1 + \theta_2 \right) \end{bmatrix} \end{eqnarray}$$
と求められます。
詳しい算出方法は、こちらの記事を参考にしてください。

この算出したヤコビ行列Jを用いて、2リンクモデルの可操作性楕円体を求めていきます。
可操作性楕円体の算出
可操作性楕円体を描くのに必要な情報として、
- 楕円体の各軸の向き
- 各軸方向の大きさ
があります。
この楕円体の軸の向きと大きさは、ヤコビ行列Jから算出できる行列Aから得ることが出来ます。
行列Aの算出
可操作性楕円体に必要な行列Aはヤコビ行列を用いて
$$ \boldsymbol{A} = \boldsymbol{J} \boldsymbol{J}^T $$
と定義します。
今回の2リンクモデルにおける行列A(=JJT)の各成分は
$$ \begin{eqnarray} \boldsymbol{A} = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} &=& \boldsymbol{J} \boldsymbol{J}^T \\ &=& \begin{bmatrix} j_{11} & j_{12} \\ j_{21} & j_{22} \end{bmatrix} \begin{bmatrix} j_{11} & j_{12} \\ j_{21} & j_{22} \end{bmatrix}^T \\ &=& \begin{bmatrix} j_{11} & j_{12} \\ j_{21} & j_{22} \end{bmatrix} \begin{bmatrix} j_{11} & j_{21} \\ j_{12} & j_{22} \end{bmatrix} \\ &=& \begin{bmatrix} {j_{11}}^2 + {j_{12}}^2 & j_{11} j_{21} + j_{12} j_{22} \\ j_{21} j_{11} + j_{22} j_{12} & {j_{21}}^2 + {j_{22}}^2 \end{bmatrix} \end{eqnarray} $$
と求めることが出来ます。
この行列Aの各成分をヤコビ行列Jの成分から求めると
$$ \begin{eqnarray} a_{11} &=& {j_{11}}^2 + {j_{12}}^2 \\ &=& \left( – L_1 \sin \left( \theta_1 \right) – L_2 \sin \left( \theta_1 + \theta_2 \right) \right)^2 + \left( – L_2 \sin \left( \theta_1 + \theta_2 \right) \right)^2 \\ a_{12} &=& j_{11} j_{21} + j_{12} j_{22} \\ &=& \left( – L_1 \sin \left( \theta_1 \right) – L_2 \sin \left( \theta_1 + \theta_2 \right) \right) \left( L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) \right) \\ &\quad& + \left( – L_2 \sin \left( \theta_1 + \theta_2 \right) \right) \left( L_2 \cos \left( \theta_1 + \theta_2 \right) \right) \\ &=& – \frac{1}{2} {L_1}^2 \sin \left( 2 \theta_1 \right) – L_1 L_2 \sin \left( 2 \theta_1 + \theta_2 \right) – {L_2}^2 \sin \left( 2 \theta_1 + 2 \theta_2 \right) \\ a_{21} &=& j_{21} j_{11} + j_{22} j_{12} \\ &=& \left( L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) \right) \left( – L_1 \sin \left( \theta_1 \right) – L_2 \sin \left( \theta_1 + \theta_2 \right) \right) \\ &\quad& + \left( L_2 \cos \left( \theta_1 + \theta_2 \right) \right) \left( – L_2 \sin \left( \theta_1 + \theta_2 \right) \right) \\ &=& – \frac{1}{2} {L_1}^2 \sin \left( 2 \theta_1 \right) – L_1 L_2 \sin \left( 2 \theta_1 + \theta_2 \right) – {L_2}^2 \sin \left( 2 \theta_1 + 2 \theta_2 \right) \\ a_{22} &=& {j_{21}}^2 + {j_{22}}^2 \\ &=& \left( L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) \right)^2 + \left( L_2 \cos \left( \theta_1 + \theta_2 \right) \right)^2 \end{eqnarray} $$
となります。
よって、可操作性楕円体を描くために求めたい行列Aは
$$ \begin{eqnarray} \boldsymbol{A} = \begin{bmatrix} \scriptsize{ \left( – L_1 \sin \left( \theta_1 \right) – L_2 \sin \left( \theta_1 + \theta_2 \right) \right)^2 + \left( – L_2 \sin \left( \theta_1 + \theta_2 \right) \right)^2 } & \scriptsize{ – \frac{1}{2} {L_1}^2 \sin \left( 2 \theta_1 \right) – L_1 L_2 \sin \left( 2 \theta_1 + \theta_2 \right) – {L_2}^2 \sin \left( 2 \theta_1 + 2 \theta_2 \right) } \\ \scriptsize{ – \frac{1}{2} {L_1}^2 \sin \left( 2 \theta_1 \right) – L_1 L_2 \sin \left( 2 \theta_1 + \theta_2 \right) – {L_2}^2 \sin \left( 2 \theta_1 + 2 \theta_2 \right) } & \scriptsize{ \left( L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) \right)^2 + \left( L_2 \cos \left( \theta_1 + \theta_2 \right) \right)^2 } \end{bmatrix} \end{eqnarray} $$
と算出することが出来ました。
固有値と固有ベクトル
この算出した行列Aの固有値と固有ベクトルを求めることで、可操作性楕円体の導出します。
行列A
$$ \boldsymbol{A} = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} $$
について、
$$ \begin{eqnarray} && \mathrm{ det } \left( \boldsymbol{A} – \lambda \boldsymbol{I} \right) = 0 \\ && \Rightarrow \begin{vmatrix} a_{11} – \lambda & a_{12} \\ a_{21} & a_{22} – \lambda \end{vmatrix} = 0 \end{eqnarray} $$
を求めることで、行列Aの固有値λと固有ベクトルvを求めます。
詳しくは次回の記事で導出します。
まとめ
今回の記事では、2リンクモデルのロボットを用いて、運動学の式から求めたヤコビ行列から可操作性楕円体を求めるための方法を紹介しました。
次回の記事では、今回の記事の続きとして、算出した行列Aから固有値と固有ベクトルを求めることで、2リンクモデルロボットの可操作性楕円体を作成したいと思います。
合わせて読みたい
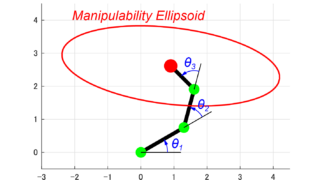
3リンクロボットアームの可操作性楕円体を求める方法を紹介しています。
























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
