スプライン曲線を用いることで、離散点を滑らかなに結ぶことが出来ます。
以前の記事では、4つの離散点を3次スプライン曲線を用いて結ぶプログラムを紹介しました。
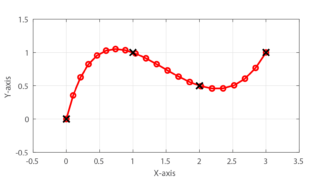
今回の記事では、このプログラムを拡張して、N+1個の離散点を通るN次スプライン曲線を書くためのプログラムを紹介します。
使用したプログラム
今回の記事で紹介するN+1個の離散的な指令点をN次スプライン曲線を用いて滑らかに補間するプログラムは下記の通りです。
X = [0.0;1.5;2.5;4.0;3.0;1.0;0.0]; % X Position Y = [0.0;0.5;0.5;1.0;2.5;2.0;1.0]; % Y Position % Calculate Variable u temp_u = (diff(X).^2+diff(Y).^2).^0.5; N = length(temp_u); u = 0; for i = 1:N u = [u;sum(temp_u(1:i))]; end % Calculate Parameters A = ones(N+1,1); for i = 1:N A = [u.^i,A]; end P_X = A\X; P_Y = A\Y; % Output Results t = 0:sum(temp_u)/100:sum(temp_u); OutX = P_X(end); OutY = P_Y(end); for i = 1:N OutX = OutX + P_X(end-i)*t.^i; OutY = OutY + P_Y(end-i)*t.^i; end Ts = 0.1; OutT = 0:Ts:(length(OutX)-1)*Ts; dOutX = diff(OutX)/Ts; ddOutX = diff(dOutX)/Ts; dOutY = diff(OutY)/Ts; ddOutY = diff(dOutY)/Ts;
このプログラムをMATLAB上で実行することで、N次スプライン曲線によるN+1個の離散点補間を実現できます。
プログラムの解説
上で紹介したMATLABプログラムについて、ステップ毎に解説していきます。
補間する指令点の定義
離散的な指令点としてX軸とY軸の値を与えます。
X = [0.0;1.5;2.5;4.0;3.0;1.0;0.0]; % X Position Y = [0.0;0.5;0.5;1.0;2.5;2.0;1.0]; % Y Positio
今回は上記のプログラムのように、ベクトルを用いてX軸、Y軸それぞれ7点の指令を定義します。
今回のプログラム内の例では、補間したいN+1個の離散点として7個の離散点を与え、補間するN次のスプラインとして6次スプライン曲線を用いています。
この入力するX軸とY軸の数を変えることで、その数に応じた次数のスプライン曲線が用いられます。
変数uの算出
次に、スプライン曲線を求める際に用いる変数ベクトルuを算出します。
% Calculate Variable u temp_u = (diff(X).^2+diff(Y).^2).^0.5; N = length(temp_u); u = 0; for i = 1:N u = [u;sum(temp_u(1:i))]; end
まず、与えられた指令点の値(XとY)から各指令点間の距離(temp_u)を算出します。
このとき、求めたベクトルtemp_uからスプライン曲線の次数Nを算出します。
そして、その算出した指令点間の距離を基に変数ベクトルuを算出します。
スプライン曲線のパラメータを算出
算出した変数ベクトルuを用いて、スプライン曲線のパラメータを求めます。
% Calculate Parameters
A = ones(N+1,1);
for i = 1:N
A = [u.^i,A];
end
P_X = A\X;
P_Y = A\Y;まず、前のステップで求めたベクトルuを用いて、行列Aを定義します。
そして、行列Aの逆行列を用いることで、各軸(X軸とY軸)のスプライン曲線パラメータ(PXとPY)を算出します。
スプライン曲線の算出
最後にN+1個の離散点を結ぶN次スプライン曲線を求めます。
% Output Results t = 0:sum(temp_u)/100:sum(temp_u); OutX = P_X(end); OutY = P_Y(end); for i = 1:N OutX = OutX + P_X(end-i)*t.^i; OutY = OutY + P_Y(end-i)*t.^i; end Ts = 0.1; OutT = 0:Ts:(length(OutX)-1)*Ts; dOutX = diff(OutX)/Ts; ddOutX = diff(dOutX)/Ts; dOutY = diff(OutY)/Ts; ddOutY = diff(dOutY)/Ts;
まず、スプライン曲線を描くための変数ベクトルtを定義します。
今回は、スプライン曲線全体を100等分してtを定義しました。
この変数ベクトルtと先に求めたN次スプライン曲線のパラメータを用いて、各軸の値(OutXとOutY)を求めます。
また今回の例では、各離散点の間隔を0.1秒(Ts=0.1)とした時の時間(OutT)、各軸の速度(dOutXとdOutY)および加速度(ddOutXとddOutY)も併せて求めています。
まとめ
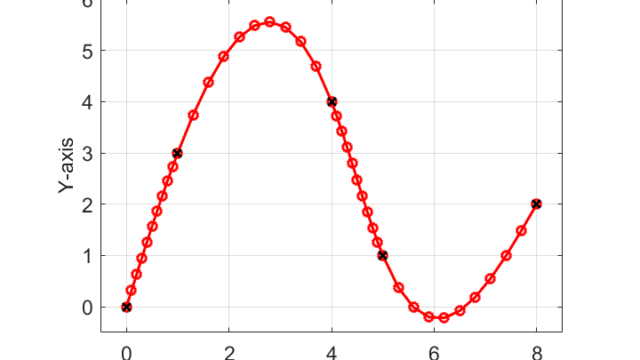
今回の記事では、N次スプライン曲線を用いてN+1個の離散点を補間するためのMATLABプログラムを紹介しました。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
