前回の記事では、制御システムのパラメータが変化した際の伝達関数の極の動きを求めて根軌跡を求めました。
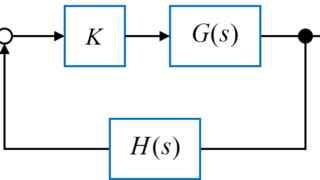
今回は、根軌跡の特徴を用いて根軌跡を描くために、点sが根軌跡上に存在するかしないかを求めていきたいと思います。
開ループ伝達関数と根軌跡
前回までのおさらいとして、開ループ伝達関数と根軌跡の関係を紹介します。
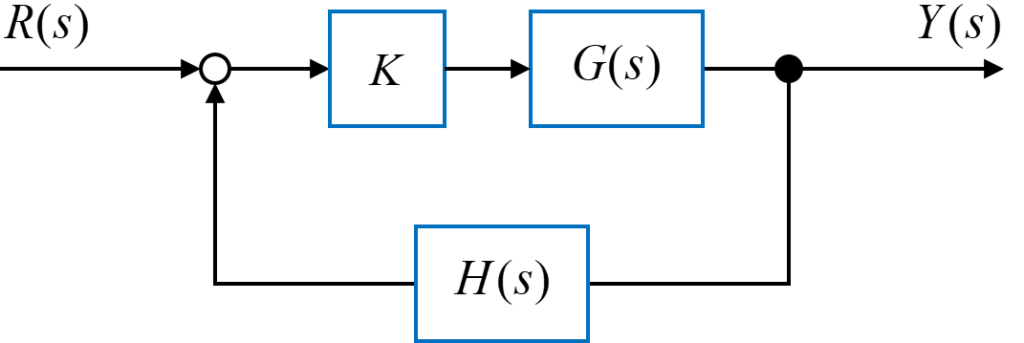
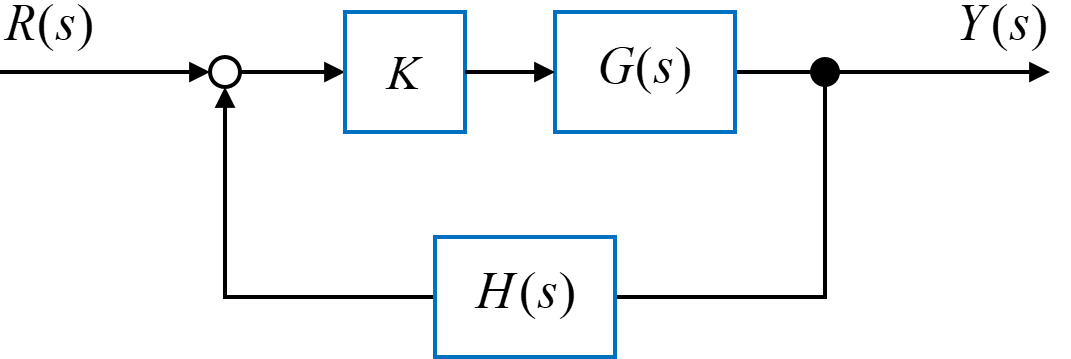
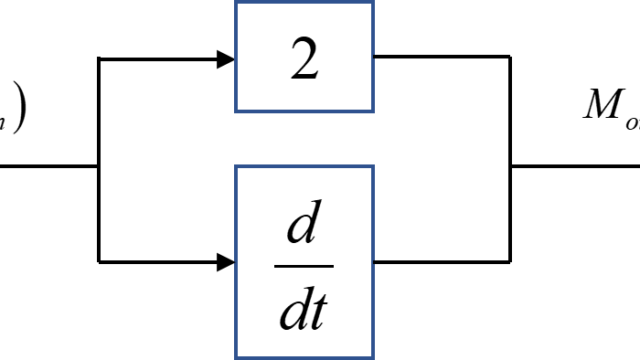
図のようなフィードバックシステムを用いて考えていきます。
このフィードバックシステム全体の伝達関数\(T(s)\)は
$$ T(s) = \frac{K G(s)}{1 + K G(s) H(s)} $$
で求めることが出来ます。
このとき根軌跡で表されるフィードバックシステムの極について、開ループ伝達関数
$$ K G(s) H(s) $$
を用いて、
$$ K G(s) H(s) = 1 \angle \left(2k+1\right) 180^{ \circ } $$
$$ k = 0, \pm 1, \pm 2, \pm 3, \cdots $$
という関係式で表すことが出来ます。
よって、開ループ伝達関数はシステムの極について
$$ \left| K G(s) H(s) \right| = 1 $$
$$ \angle K G(s) H(s) = \left(2k+1\right) 180^{ \circ } $$
$$ K = \frac{1}{|G(s)| |H(s)|} $$
という特徴を持ちます。
開ループ伝達関数と極と根軌跡
開ループ伝達関数を根軌跡の特徴を用いて、ある任意の点が根軌跡上に存在するかしないかを求めていきます。
システムの開ループ伝達関数が
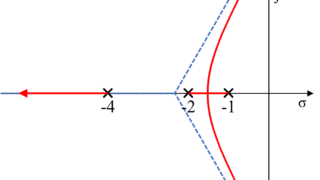
$$ K G(s) H(s) = \frac{K (s+1)(s+2)}{(s+3)(s+4)} $$
で与えられた場合を考えます。
点\(-3 + j2\)の場合
点\(-3 + j2\)について、フィードバックシステムのパラメータ\(K\)を変化させた際の極になり得るか、つまり根軌跡上に存在するかを考えます。
制御システムの開ループ伝達関数の極および零点の位置から対象となる点\(-3 + j2\)への角度を計算します。
零点\(-1\)と対象の点\(-3 + j2\)とでなす角\(\theta_1\)は、
$$ \theta_1 = \arctan \left(\frac{2-0}{-3-(-1)}\right) $$
$$ = \arctan \left(\frac{2}{-2}\right) $$
と求めることが出来ます。
同様に、残りの零点\(-2\)となす角\(\theta_2\)、極\(-3\)と\(-4\)となす角\(\theta_3\)と\(\theta_4\)は
$$ \theta_2 = \arctan \left(\frac{2}{-1}\right) $$
$$ \theta_3 = \arctan \left(\frac{2}{0}\right) $$
$$ \theta_4 = \arctan \left(\frac{2}{1}\right) $$
と求められます。
これらの角度(\(\theta_1,\theta_2,\theta_3,\theta_4\))について、解ループ伝達関数の極の特徴より、足し合わせた結果が\(180^{ \circ }\)になっていれば、この対象の点はシステムの伝達関数の極になりうる、つまり根軌跡上に存在すると言えます。
4つの角度(\(\theta_1,\theta_2,\theta_3,\theta_4\))を足し合わせると、
$$ {\theta}_1 + {\theta}_2 – {\theta}_3 – {\theta}_4 = \arctan \left(\frac{2}{-2}\right) + \arctan \left(\frac{2}{-1}\right) – \arctan \left(\frac{2}{0}\right) – \arctan \left(\frac{2}{1}\right) $$
$$ = 135^{ \circ } + 116.6^{ \circ } – 90^{ \circ } – 63.4^{ \circ } = 98.1^{ \circ } $$
となります。
よって、\(180^{ \circ }\)ではないので、この点\(-3 + j2\)は根軌跡上に存在しないことが分かりました。
点\(-3 + j\frac{\sqrt{2}}{2}\)の場合
次に点\(-3 + j\frac{\sqrt{2}}{2}\)について、フィードバックシステムのパラメータ\(K\)を変化させた際の極になり得るか、根軌跡上に存在するかを考えます。
開ループ伝達関数の極と零点から対象の点\( -3 + j \frac{\sqrt{2}}{2} \)への角度を求めて足し合わせると、
$$ {\theta}_1 + {\theta}_2 – {\theta}_3 – {\theta}_4 = \arctan \left(\frac{\frac{\sqrt{2}}{2}}{-2}\right) + \arctan \left(\frac{\frac{\sqrt{2}}{2}}{-1}\right) – \arctan \left(\frac{\frac{\sqrt{2}}{2}}{0}\right) – \arctan \left(\frac{\frac{\sqrt{2}}{2}}{1}\right) $$
$$ = 160.5^{ \circ } + 144.7^{ \circ } – 90^{ \circ } – 35.3^{ \circ } = 180^{ \circ } $$
となり、\(180^{ \circ }\)となるため、この点\(-3 + j\frac{\sqrt{2}}{2}\)は根軌跡上に存在することが分かりました。
また、この点\(-3 + j\frac{\sqrt{2}}{2}\)が極となるときのゲイン\(K\)についても、開ループ伝達関数の極の特徴から求めることが出来ます。
点\(-3 + j\frac{\sqrt{2}}{2}\)が極となるときのゲイン\(K\)は、
$$ K = \frac{1}{|G(s)| |H(s)|} = \frac{(s+3)(s+4)}{(s+1)(s+2)} $$
$$ = \frac{(-3 + j\frac{\sqrt{2}}{2}+3)(-3 + j\frac{\sqrt{2}}{2}+4)}{(-3 + j\frac{\sqrt{2}}{2}+1)(-3 + j\frac{\sqrt{2}}{2}+2)} = \frac{1}{3} $$
と求めることが出来ます。
また、このゲイン\(K\)は対象の点と開ループ伝達関数の極と零点の距離からも求めることが出来ます。
開ループ伝達関数の極と零点(\(-1,-2,-3,-4\))から対象の点\(-3 + j\frac{\sqrt{2}}{2}\)までの距離をそれぞれ\(L_1\)、\(L_2\)、\(L_3\)、\(L_4\)とすると、ゲイン\(K\)は
$$ K = \frac{L_3 L_4}{L_1 L_2} $$
$$ = \frac{0.7071 \cdot 1.2247}{2.1213 \cdot 1.2247} = 0.3333 = \frac{1}{3} $$
と求めることが出来ます。
まとめ
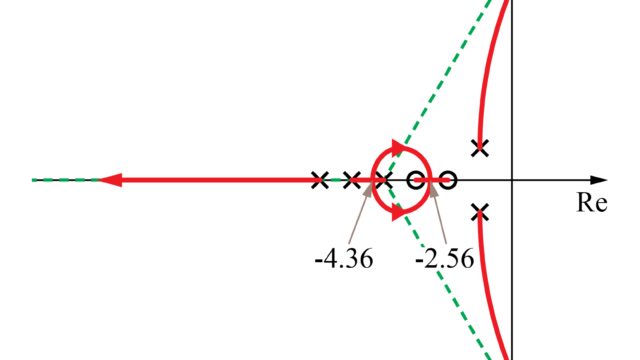
今回は、点sが根軌跡上に存在するかしないかを根軌跡の特徴を用いて求める方法を紹介しました。
複素平面上の全ての点において、今回紹介した方法を用いることで根軌跡を作成することが出来ますが、とても大変で現実的ではありません。
そこで、次回は実際に根軌跡を描くために必要な根軌跡の持つ特徴を紹介していきたいと思います。
























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
