本シリーズでは、制御工学で学ぶ基本的な知識から実際の応用例までを、なるべく分かりやすく解説しています。

以前の記事で、常微分方程式で与えられた線形システムの状態方程式の一般解を、固有値と固有ベクトルを用いて求める方法を紹介しました。

今回は、具体的な例として2質量のシステムを用いて、実際にシステムの解を固有値・固有ベクトルを使って求めていきたいと思います。
線形システムと固有値・固有ベクトルによる解法
線形システムの状態方程式は
$$ \dot{\boldsymbol{ x }} = \boldsymbol{ A } \boldsymbol{ x } $$
と表されます。
ここで、xはn次元の状態変数ベクトルで、Aはn×nの行列で状態変数ベクトルxがどのように変化するかを表しています。
この行列Aについて固有値λと固有ベクトルζを求めます。
行列Aの固有値λ1, λ2, λ3,… λnと固有ベクトルζ1, ζ2, ζ3,…, ζnについて
$$ \begin{eqnarray} \boldsymbol{ T } &=& \begin{bmatrix} \boldsymbol{ \zeta_1 } & \boldsymbol{ \zeta_2 } & \boldsymbol{ \zeta_3 } & \cdots & \boldsymbol{ \zeta_n } \end{bmatrix} \\ \boldsymbol{ D } &=& \begin{bmatrix} \lambda_1 & & & & 0 \\ & \lambda_2 & & & \\ & & \lambda_3 & & \\ & & & \ddots & \\ 0 & & & & \lambda_n \end{bmatrix} \end{eqnarray} $$
という形で行列Tと行列Dを定義します。
まず、固有ベクトルζによる行列Tを用いて
$$ \boldsymbol{ z } (0) = \boldsymbol{ T }^{-1} \boldsymbol{ x } (0) $$
のように、状態ベクトルxの初期条件をベクトルzに変換します。
そして、固有値λによる行列Dを用いて
$$ \boldsymbol{ z } (t) = e^{\boldsymbol{ D } t} \boldsymbol{ z } (0) $$
と、変換後の座標空間での一般解zを求めます。
最後に、また行列Tを用いて
$$ \boldsymbol{ x } (t) = \boldsymbol{ T } \boldsymbol{ z } (t) $$
のように、もとの座標空間に戻して、一般解xを算出します。
2質量システムと状態方程式
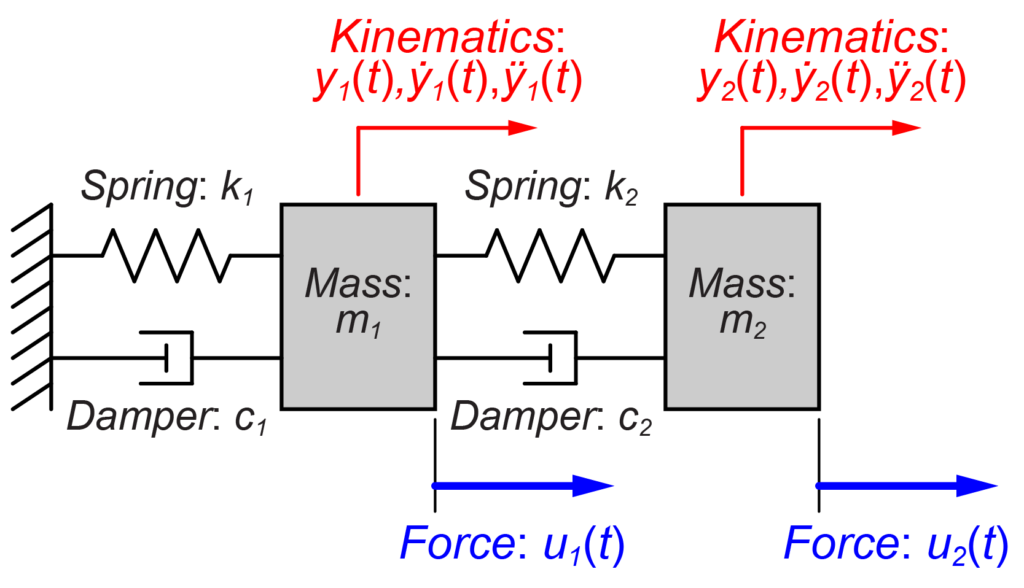
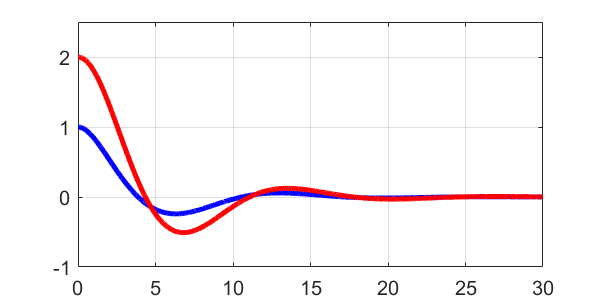
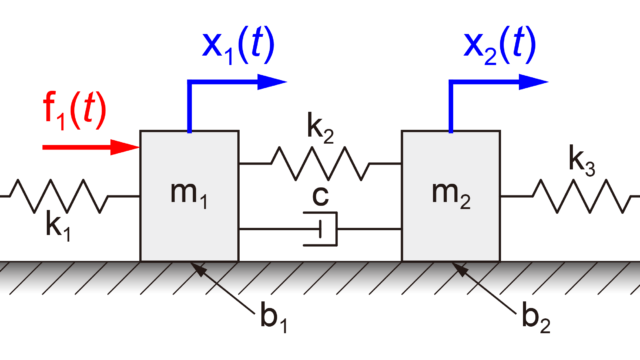
今回は、上の図のような2つの質量がそれぞれバネとダンパーで接続されたモデルを取り扱います。
このモデルの運動方程式は、
$$ \begin{eqnarray} \left\{ \begin{array}{l} m_1 \ddot{y_1}(t) = u_1(t) – k_1 y_1(t) – c_1 \dot{y_1}(t) + k_2 \left( y_2(t) – y_1(t) \right) + c_2 \left( \dot{y_2}(t) – \dot{y_1}(t) \right) \\ m_2 \ddot{y_2}(t) = u_2(t) – k_2 \left( y_2(t) – y_1(t) \right) – c_2 \left( \dot{y_2}(t) – \dot{y_1}(t) \right) \end{array} \right. \end{eqnarray} $$
となります。
今回は入力(u1とu2)は無いものとして考えます。
このシステムの状態を示す状態ベクトル\(\boldsymbol{x}\)は
$$ \boldsymbol{x} = \begin{bmatrix} y_1 \\ \dot{y_1} \\ y_2 \\ \dot{y_2} \end{bmatrix} $$
と定義します。
この時の状態方程式は、モデルの運動方程式より
$$ \boldsymbol{\dot{x}} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ – \frac{k_1+k_2}{m_1} & – \frac{c_1+c_2}{m_1} & \frac{k_2}{m_1} & \frac{c_2}{m_1} \\ 0 & 0 & 0 & 1 \\ \frac{k_2}{m_2} & \frac{c_2}{m_2} & – \frac{k_2}{m_2} & – \frac{c_2}{m_2} \end{bmatrix} \boldsymbol{x} $$
と表すことが出来ます。
質量、ばね、ダンパの値がそれぞれ
$$ \left\{ \begin{array}{l} m_1 = 10 \ [kg] \\ m_2 = 5 \ [kg] \end{array} \right. , \ \left\{ \begin{array}{l} k_1 = 6 \ [N/m] \\ k_2 = 2 \ [N/m] \end{array} \right. , \ \left\{ \begin{array}{l} c_1 = 8 \ [N/(m/s)] \\ c_2 = 4 \ [N/(m/s)] \end{array} \right. $$
とすると、今回の2質量システムの状態方程式は、各々の値を代入して
$$ \boldsymbol{\dot{x}} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ – \frac{4}{5} & – \frac{6}{5} & \frac{1}{5} & \frac{2}{5} \\ 0 & 0 & 0 & 1 \\ \frac{2}{5} & \frac{4}{5} & – \frac{2}{5} & – \frac{4}{5} \end{bmatrix} \boldsymbol{x} $$
となります。
固有値と固有ベクトルによる解析
では、実際に固有値と固有ベクトルを用いて、状態ベクトルxの初期条件x(0)が
$$ \boldsymbol{x} (0) = \begin{bmatrix} 1 \\ 0 \\ 2 \\ 0 \end{bmatrix} $$
と与えられた場合の、システムに含まれる2つの質量の運動を求めていきたいと思います。
この初期条件x(0)は、質量m1の位置が1[m]で質量m2の位置が2[m]を意味しています。
まず初めに、行列Aの固有値と固有ベクトルを求めます。
行列A
$$ \begin{bmatrix} 0 & 1 & 0 & 0 \\ – \frac{4}{5} & – \frac{6}{5} & \frac{1}{5} & \frac{2}{5} \\ 0 & 0 & 0 & 1 \\ \frac{2}{5} & \frac{4}{5} & – \frac{2}{5} & – \frac{4}{5} \end{bmatrix} $$
の固有値λと固有ベクトルζを求めると
$$ \begin{eqnarray} \lambda_1 = -0.7891+0.5368i, \ \boldsymbol{\zeta_1} = \begin{bmatrix} 0.4635-0.1192i \\ -0.3018+0.3429 \\ -0.5425 \\ 0.4281-0.2912 \end{bmatrix} \\ \lambda_2 = -0.7891-0.5368i, \ \boldsymbol{\zeta_2} = \begin{bmatrix} 0.4635+0.1192i \\ -0.3018-0.3429 \\ -0.5425 \\ 0.4281+0.2912 \end{bmatrix} \\ \lambda_3 = -0.2109+0.4680i, \ \boldsymbol{\zeta_3} = \begin{bmatrix} 0.3360+0.0833i \\ -0.1099+0.1397 \\ 0.8195 \\ -0.1728+0.3835 \end{bmatrix} \\ \lambda_4 = -0.2109-0.4680i, \ \boldsymbol{\zeta_4} = \begin{bmatrix} 0.3360-0.0833i \\ -0.1099-0.1397 \\ 0.8195 \\ -0.1728-0.3835 \end{bmatrix} \\ \end{eqnarray} $$
となります。
これより、固有ベクトルζによる行列Tと固有値λによる行列Dは
$$ \begin{eqnarray} \boldsymbol{ T } &=& \begin{bmatrix} 0.4635-0.1192i & 0.4635+0.1192i & 0.3360+0.0833i & 0.3360-0.0833i \\ -0.3018+0.3429 & -0.3018-0.3429 & -0.1099+0.1397 & -0.1099-0.1397 \\ -0.5425 & -0.5425 & 0.8195 & 0.8195 \\ 0.4281-0.2912 & 0.4281+0.2912 & -0.1728+0.3835 & -0.1728-0.3835 \end{bmatrix} \\ \boldsymbol{ D } &=& \begin{bmatrix} -0.7891+0.5368i & 0 & 0 &0 \\ 0 & -0.7891-0.5368i & 0 & 0 \\ 0 & 0 & -0.2109+0.4680i & 0 \\ 0 & 0 & 0 & -0.2109-0.4680i \end{bmatrix} \end{eqnarray} $$
となります。
次に、行列Tを用いて状態ベクトルxの初期条件をベクトルzの初期条件に変換すると
$$ \begin{eqnarray} \boldsymbol{ z } (0) &=& \boldsymbol{ T }^{-1} \boldsymbol{ x } (0) \\ &=& \begin{bmatrix} 0.4635-0.1192i & 0.4635+0.1192i & 0.3360+0.0833i & 0.3360-0.0833i \\ -0.3018+0.3429 & -0.3018-0.3429 & -0.1099+0.1397 & -0.1099-0.1397 \\ -0.5425 & -0.5425 & 0.8195 & 0.8195 \\ 0.4281-0.2912 & 0.4281+0.2912 & -0.1728+0.3835 & -0.1728-0.3835 \end{bmatrix}^{-1} \begin{bmatrix} 1 \\ 0 \\ 2 \\ 0 \end{bmatrix} \\ &=& \begin{bmatrix} 0.0922-0.2278i \\ 0.0922+0.2278i \\ 1.2812-0.6474i \\ 1.2812+0.6474i \end{bmatrix} \end{eqnarray} $$
のように求めることが出来ます。
そして、固有値λによる行列Dを用いて、変換後の座標空間での一般解zを求めていきます。
一般解zの1つ目の要素z1について、一般解z1(t)は
$$ \begin{eqnarray} z_1 (t) &=& e^{\lambda_1 t} z_1(0) \\ &=& e^{(-0.7891+0.5368i) t} (0.0922-0.2278i) \end{eqnarray} $$
と、時間tについての関数として求めることが出来ます。
同様に、残りの要素z2, z3, z4ついても
$$ \begin{eqnarray} z_2 (t) &=& e^{(-0.7891-0.5368i) t} (0.0922+0.2278i) \\ z_3 (t) &=& e^{(-0.2109+0.4680i) t} (1.2812-0.6474i) \\ z_4 (t) &=& e^{(-0.2109-0.4680i) t} (1.2812+0.6474i) \end{eqnarray} $$
のように、時間tについての一般解を算出できます。
最後に、求めた時間tについての解z(t)を、行列Tを用いて
$$ \boldsymbol{ x } (t) = \boldsymbol{ T } \boldsymbol{ z } (t) $$
と、もとの座標空間に戻して、一般解xを算出します。
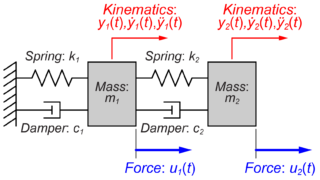
実際に、時間tについて30秒まで求めた結果は上の図のようになります。
縦軸が各質量の位置[m]で横軸が時間[sec]です。
システムに外力がなく、ダンパーが含まれているため、質量m1(青線)と質量m2(赤線)の位置は振動しながら徐々に0に近づくことが分かります。
まとめ
今回は、実際に2質量のシステムを具体例として取り扱い、システムの解を固有値・固有ベクトルを使って求める方法を紹介しました。
今回紹介したように、固有値と固有ベクトルを用いることで、難しい微分方程式を解く必要がなく、線形システムの解を簡単な式で求めることが出来ました。
























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
