本シリーズでは、制御工学で学ぶ基本的な知識から実際の応用例までを、なるべく分かりやすく解説しています。
前々回、前回の記事では、常微分方程式で表された線形システムの状態方程式の一般解と、固有値と固有ベクトルを用いて計算量を減らす方法について紹介しました。


今回の記事では、前回求めたz座標に変換後の解から、実際に求めたい線形システムの状態x(t)を求める方法を紹介していきたいと思います。
常微分方程式を固有値・固有ベクトルで解く
z座標を用いることで、簡単に線形システムの微分方程式をz座標空間で解くことが出来ました。
では、z座標での解からx座標での解を求めるために、x座標における
$$ \begin{eqnarray} \begin{array}{l} \dot{\boldsymbol{ x }} = \boldsymbol{ A } \boldsymbol{ x } \\ \Rightarrow \boldsymbol{ x } (t) = e^{\boldsymbol{ A } t} \boldsymbol{ x } (0) \end{array} \end{eqnarray} $$
とz座標における
$$ \begin{eqnarray} \begin{array}{l} \dot{\boldsymbol{ z }} = \boldsymbol{ D } \boldsymbol{ z } \\ \Rightarrow \boldsymbol{ z } (t) = e^{\boldsymbol{ D } t} \boldsymbol{ z } (0) \end{array} \end{eqnarray} $$
との関係を示したいと思います。
自然数eの行列A乗を行列D乗に変換する
行列Aと行列Dの関係式より
$$ \begin{eqnarray} \begin{array}{l} \boldsymbol{ A } \boldsymbol{ T } = \boldsymbol{ T } \boldsymbol{ D } \\ \boldsymbol{ A } = \boldsymbol{ T } \boldsymbol{ D } \boldsymbol{ T }^{-1} \end{array} \end{eqnarray} $$
のように行列Aについての式を求めます。
この式を、状態変数xの座標におけるテイラー展開を用いた一般解に含まれる
$$ e^{\boldsymbol{ A } t} = \boldsymbol{ I } + \boldsymbol{ A } t + \frac{\boldsymbol{ A }^2 t^2}{2!} + \frac{\boldsymbol{ A }^3 t^3}{3!} + \cdots $$
に代入すると
$$ \begin{eqnarray} \begin{array}{l} e^{\boldsymbol{ T } \boldsymbol{ D } \boldsymbol{ T }^{-1} t} = \boldsymbol{ T } \boldsymbol{ T }^{-1} + \boldsymbol{ T } \boldsymbol{ D } \boldsymbol{ T }^{-1} t + \boldsymbol{ T } \boldsymbol{ D } \boldsymbol{ T }^{-1} \boldsymbol{ T } \boldsymbol{ D } \boldsymbol{ T }^{-1} \dfrac{t^2}{2!} + + \cdots \\ = \boldsymbol{ T } \boldsymbol{ T }^{-1} + \boldsymbol{ T } \boldsymbol{ D } \boldsymbol{ T }^{-1} t + \boldsymbol{ T } \boldsymbol{ D }^2 \boldsymbol{ T }^{-1} \dfrac{t^2}{2!} + \boldsymbol{ T } \boldsymbol{ D }^3 \boldsymbol{ T }^{-1} \dfrac{t^3}{3!} + \cdots \end{array} \end{eqnarray} $$
のように、まとめることが出来ます。
この変換は
$$ \boldsymbol{ A }^n = \boldsymbol{ T } \boldsymbol{ D }^n \boldsymbol{ T }^{-1} $$
が成り立つことからも分かると思います。
最後に、まとめた式のすべての項について、左側から行列Tが、右側から行列Tの逆行列が掛けられていることが分かります。
よって先に求めた式から、自然数eのAt乗は
$$ \begin{eqnarray} e^{\boldsymbol{ A } t} &=& e^{\boldsymbol{ T } \boldsymbol{ D } \boldsymbol{ T }^{-1} t} \\ &=& \boldsymbol{ T } \left[ \boldsymbol{ I } + \boldsymbol{ D } t + \frac{\boldsymbol{ D }^2 t^2}{2!} + \frac{\boldsymbol{ D }^3 t^3}{3!} + \cdots \right] \boldsymbol{ T }^{-1} \\ &=& \boldsymbol{ T } e^{\boldsymbol{ D } t} \boldsymbol{ T }^{-1} \end{eqnarray}$$
のように、自然数eのDt乗を用いた式で求められることが分かりました、
行列Aのn乗とは違い、行列Dのn乗は行列Dが対角行列なので、簡単に計算することが出来ます。
線形システムの状態x(t)を求める
以上の結果をもとに、実際に求めたい線形システムの状態x(t)を求めていきます。
線形システムの微分方程式の一般解
$$ \boldsymbol{ x } (t) = e^{\boldsymbol{ A } t}\boldsymbol{ x } (0) $$
について
$$ e^{\boldsymbol{ A } t} = \boldsymbol{ T } e^{\boldsymbol{ D } t} \boldsymbol{ T }^{-1} $$
なので
$$ \boldsymbol{ x } (t) = \boldsymbol{ T } e^{\boldsymbol{ D } t} \boldsymbol{ T }^{-1} \boldsymbol{ x } (0) $$
となります。
x(0)は状態ベクトルの初期条件です。
ここで
$$ \begin{eqnarray} \begin{array}{l} \boldsymbol{ x } = \boldsymbol{ T } \boldsymbol{ z } \\ \Rightarrow \boldsymbol{ z } = \boldsymbol{ T }^{-1} \boldsymbol{ x } \end{array} \end{eqnarray} $$
より
$$ \boldsymbol{ x } (t) = \boldsymbol{ T } e^{\boldsymbol{ D } t} \boldsymbol{ z } (0) $$
となります。
さらに
$$ \boldsymbol{ z } (t) = e^{\boldsymbol{ D } t} \boldsymbol{ z } (0) $$
なので
$$ \boldsymbol{ x } (t) = \boldsymbol{ T } \boldsymbol{ z } (t) $$
のように、z座標空間での解であるz(t)から、実際に求めたい状態変数ベクトルxの一般解x(t)を求めることが出来ました。
先に示した通り、z(t)は簡単に計算することが出来ます。
そして、求めたz(t)と行列Tを用いることで、複雑な行列式を解かずにx(t)を求めることが出来ました。
まとめ
前々回から今回までの記事では、固有値と固有ベクトルを用いて、複雑な計算が必要となる常微分方程式で表された線形システムを、簡単な計算のみで解析する方法を紹介しました。
固有値と固有ベクトルを用いることで、計算量をかなり抑えることが出来ます。
もちろん、すべての動的システムに適応できるわけではありませんが、大体のシステムには個の法則が成り立ちます。
合わせて読みたい
今回の手法を2質量-ばね-ダンパーのシステムに応用した場合は、こちらの記事を参考にしてください。





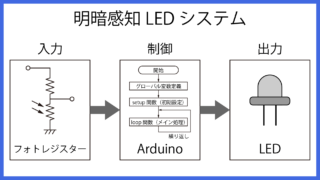
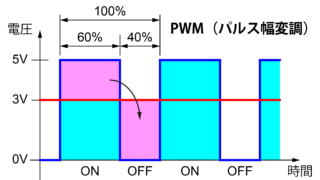
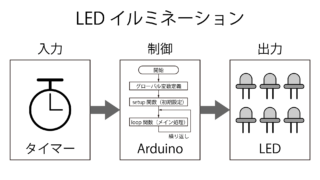
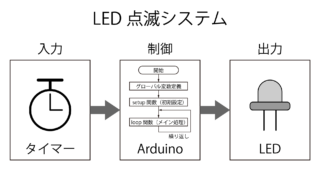
 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
