入力が与えられた質量-ばね-ダンパーシステムの応答をラプラス変換を用いて求めていきます。
前回の記事では、インパルス応答について紹介しました。

今回は、ステップ入力を与えた場合のシステムの応答を求めていきます。
システムの運動方程式
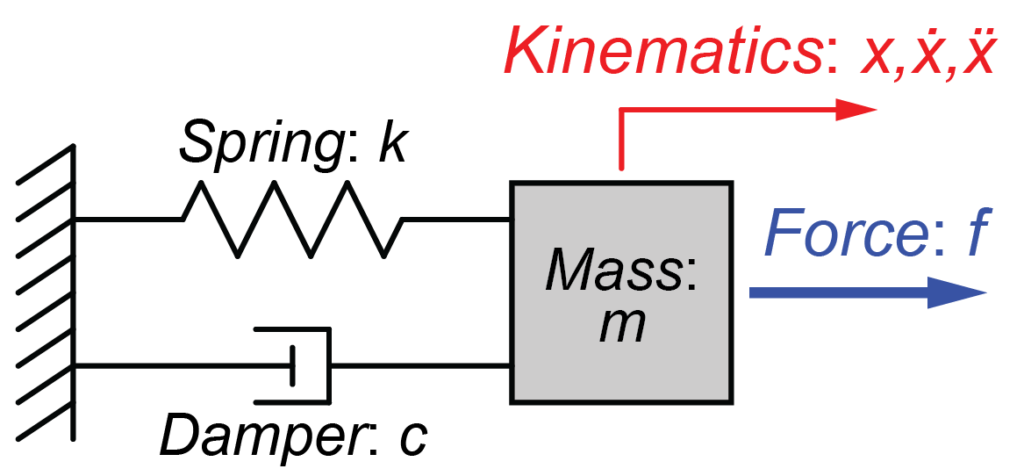
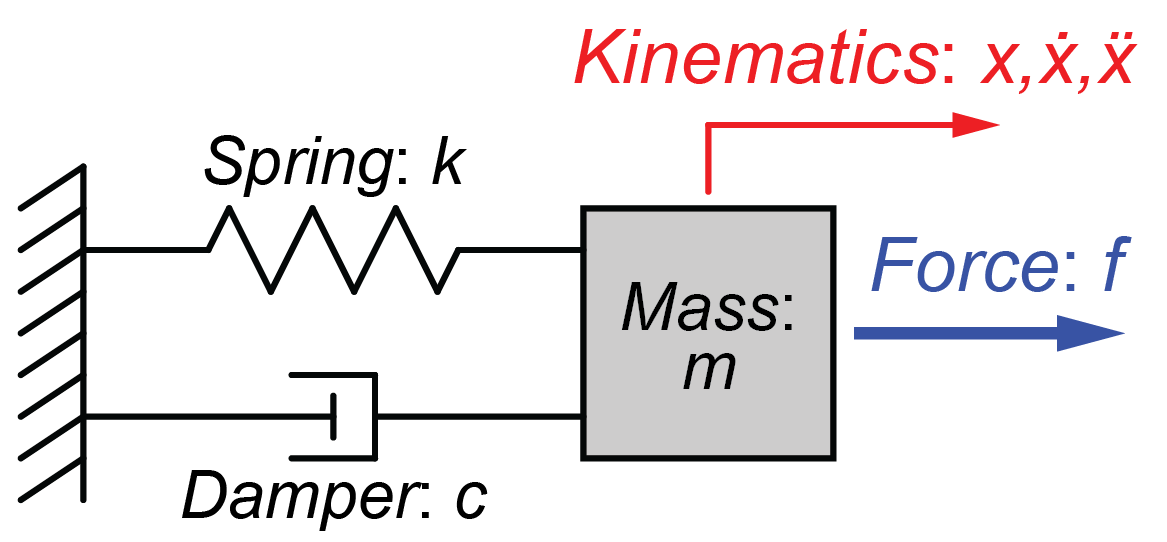
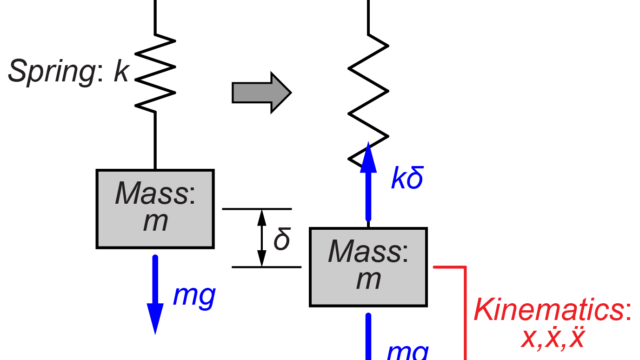
図のような質量\(m\)とばね\(k\)、ダンパー\(c\)からなる2次系システムに入力\(f(t)\)が与えられた時の運動方程式は、
$$ \ddot{x}(t) + 2 \zeta \omega_n \dot{x}(t) + \omega_n^2 x(t) = \frac{f(t)}{m} $$
と表すことが出来ます。ここで、各係数は
$$ \omega_n = \sqrt{ \frac{k}{m} } $$
$$ \zeta = \frac{c}{2 \sqrt{k m}} $$
となります。
詳しくはこちらの記事を参考にしてください。

ステップ応答
ステップ応答とは、ステップ信号をシステムに入力した際のシステムの出力のことです。
ステップ信号とは、
- ある時刻で
- 0から目標値まで立ち上がる
階段状の信号のことです。
ステップ入力\(f(t)\)の振幅を\(F_0\)とすると、
$$ \begin{eqnarray} f (t) = \begin{cases} F_0 & ( t \geq 0 ) \\ 0 & ( t \lt 0 ) \end{cases}\end{eqnarray} $$
と表されます。
このステップ信号をシステムの運動方程式に代入して、ラプラス変換を用いてシステムの運動\(x(t)\)を求めていきます。
ステップ応答のラプラス変換
ステップ応答が入力されたシステムの運動方程式をラプラス変換すると、
$$ s^2 X(s) + 2 \zeta \omega_n s X(s) + \omega_n^2 X(s) = \frac{\frac{F_0}{m}}{s} $$
となります。
これより、
$$ X(s) = \frac{\frac{F_0}{m}}{s \left(s^2 + 2 \zeta \omega_n s + \omega_n^2 \right)} $$
と表すことが出来ます。
この\(X(s)\)について、
$$ X(s) = \frac{\frac{F_0}{m}}{s \left(s^2 + 2 \zeta \omega_n s + \omega_n^2 \right)} $$
$$ \Rightarrow X(s) = \frac{\frac{F_0}{m}}{s \left( \left( s + \zeta \omega_n \right)^2 + \omega_d^2\right)} $$
と変換します。ここで、
$$ \omega_d = \omega_n \sqrt{1 – \zeta^2} $$
とします。
これより、右辺を変形して
$$ X(s) = \frac{F_0}{m} \frac{1}{s \left( \left( s + \zeta \omega_n \right)^2 + {\omega_d}^2\right)} $$
$$ \Rightarrow \frac{1}{s \left( \left( s + \zeta \omega_n \right)^2 + {\omega_d}^2\right)} = \frac{A}{s} + \frac{B s + C}{\left( s + \zeta \omega_n \right)^2 + {\omega_d}^2} $$
とした時、各係数(A、BおよびC)を示す関係式は、
$$ A \left( \left( s + \zeta \omega_n \right)^2 + {\omega_d}^2\right) + B s^2 + C s = 1$$
$$ \begin{eqnarray} \Rightarrow \begin{cases} s^2 : & A+B=0 \\ s^1 : & A \cdot 2\zeta\omega_n + C = 0 \\ s^0 : & A \left( \left(\zeta \omega_n \right)^2 + {\omega_d}^2\right) = 1 \end{cases}\end{eqnarray} $$
となります。よって、この3式を連立方程式として解くと
$$ A = \frac{1}{{\omega_n}^2} $$
$$ B = – \frac{1}{{\omega_n}^2} $$
$$ C = – \frac{2 \zeta}{\omega_n} $$
となります。
よって、先ほどの\(X(s)\)についての式は、
$$ X(s) = \frac{F_0}{m} \left( \frac{\frac{1}{{\omega_n}^2} }{s} – \frac{\frac{1}{{\omega_n}^2} s + \frac{2 \zeta}{\omega_n}}{\left( s + \zeta \omega_n \right)^2 + {\omega_d}^2} \right) $$
する表すことが出来ます。
この複素数領域\(s\)での式を時間領域\(t\)に逆ラプラス変換すると、
$$ x(t) = \frac{F_0}{k} \left( 1 – e^{-\zeta \omega_n t} \left( \cos \left( \omega_d t \right) + \frac{\zeta \omega_n}{\omega_d} \sin \left( \omega_d t \right) \right) \right) $$
とシステムの運動を数式で表すことが出来ました。
シミュレーション結果
実際の値を求めた運動の式に代入することで、システムのステップ応答を求めてみます。
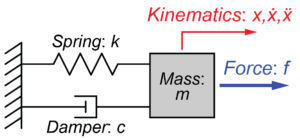
今回のシステムの各パラメータを
$$ m = 1 [kg] $$
$$ c = 2 [N/(m/s)] $$
$$ k = 10 [N/m] $$
$$ A = 0.5 [N] $$
とした時の出力は先程の式に代入すると、
$$ x(t) = 0.05 \left( 1 – e^{- t} \left( \cos \left( 3 t \right) + \frac{1}{3} \sin \left( 3 t \right) \right) \right) $$
となります。
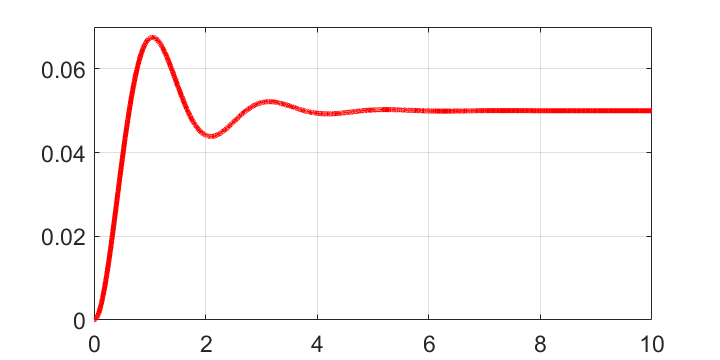
グラフから、時刻\(t=0\)で入力されたステップ信号によりシステムの出力が振動しながら増加したのち、その後は徐々に振動の幅が減少して安定した値(定常値=0.05)に近づくことが分かります。
まとめ
今回は、ステップ信号が入力として質量-ばね-ダンパーモデルに与えられた時のシステムの応答(ステップ応答)を求めるために、ラプラス変換を用いた算出方法を紹介をしました。























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
