伝達関数を用いることで、システムの応答を求めたり、制御パラメータを決定したりすることが出来ます。
この制御工学において重要である伝達関数の求め方を理解するためには、様々なケースを学ぶことが大切です。
以前の記事では、摩擦を含む3自由度システムの運動方程式を求める方法を紹介しました。

今回の記事では、3自由度系の伝達関数を運動方程式から導出する方法を紹介します。
3自由度システムと運動方程式
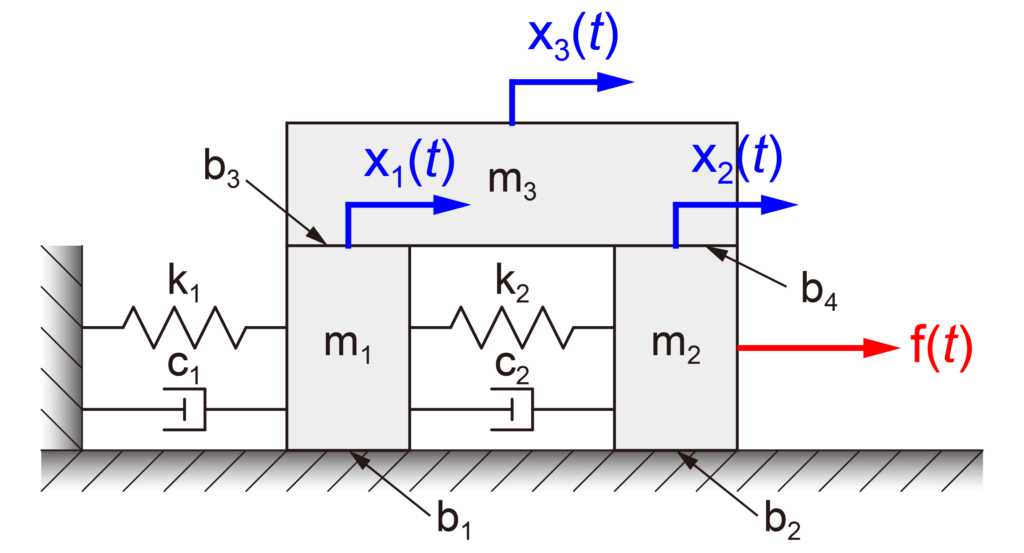
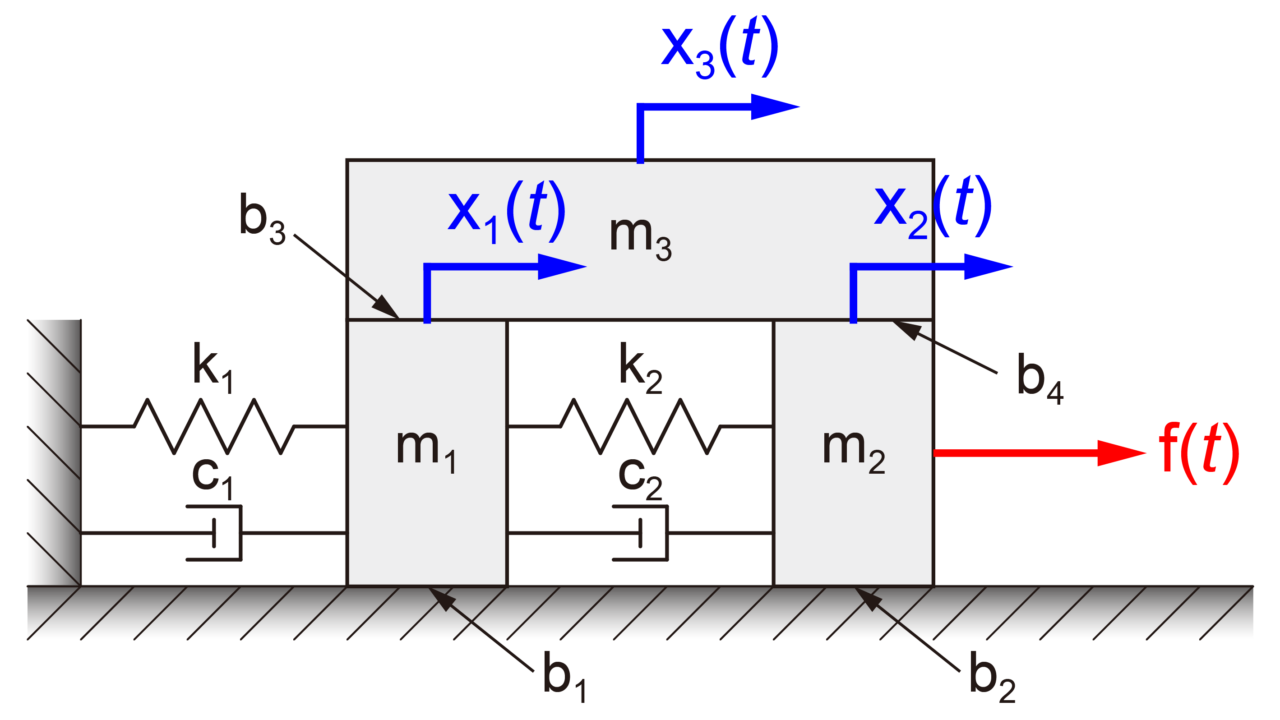
今回の記事では、上の図のような3自由度の質量-ばね-ダンパーシステムについて考えます。
今回のモデルでは、3質量の他にばねとダンパー、床と質量同士の摩擦を考慮します。
この3自由度系モデルの運動方程式は下式で表されます。
$$ \begin{eqnarray} \left\{ \begin{array}{l} m_1 \ddot{x}_1(t) + \left( c_1 + c_2 + b_1 + b_3 \right) \dot{x}_1(t) + \left( k_1 + k_2 \right) x_1(t) – c_2 \dot{x}_2(t) – k_2 x_2(t) – b_3 \dot{x}_3(t) &=& 0 \\ m_2 \ddot{x}_2(t) + \left( c_2 + b_2 + b_4 \right) \dot{x}_2(t) + k_2 x_2(t) – c_2 \dot{x}_1(t) – k_2 x_1(t) – b_4 \dot{x}_3(t) &=& f(t) \\ m_3 \ddot{x}_3(t) + \left( b_3 + b_4 \right) \dot{x}_3(t) – b_3 \dot{x}_1(t) – b_4 \dot{x}_2(t) &=& 0 \end{array} \right. \end{eqnarray} $$
この運動方程式から、入力に対する各質量の運動を表す伝達関数を求めていきます。
運動方程式をラプラス変換
システムの伝達関数を求めるために、前回求めた運動方程式をラプラス変換を用いて時間領域から周波数領域に変換します。
時間領域tで表される運動方程式
$$ \begin{eqnarray} \left\{ \begin{array}{l} m_1 \ddot{x}_1(t) + \left( c_1 + c_2 + b_1 + b_3 \right) \dot{x}_1(t) + \left( k_1 + k_2 \right) x_1(t) – c_2 \dot{x}_2(t) – k_2 x_2(t) – b_3 \dot{x}_3(t) &=& 0 \\ m_2 \ddot{x}_2(t) + \left( c_2 + b_2 + b_4 \right) \dot{x}_2(t) + k_2 x_2(t) – c_2 \dot{x}_1(t) – k_2 x_1(t) – b_4 \dot{x}_3(t) &=& f(t) \\ m_3 \ddot{x}_3(t) + \left( b_3 + b_4 \right) \dot{x}_3(t) – b_3 \dot{x}_1(t) – b_4 \dot{x}_2(t) &=& 0 \end{array} \right. \end{eqnarray} $$
に対してラプラス変換を用いることで
$$ \begin{eqnarray} \left\{ \begin{array}{l} m_1 s^2 X_1(s) + \left( c_1 + c_2 + b_1 + b_3 \right) s X_1(s) + \left( k_1 + k_2 \right) X_1(s) – c_2 s X_2(s) – k_2 X_2(s) – b_3 s X_3(s) &=& 0 \\ m_2 s^2 X_2(s) + \left( c_2 + b_2 + b_4 \right) s X_2(s) + k_2 X_2(s) – c_2 s X_1(s) – k_2 X_1(s) – b_4 s X_3(s) &=& F(s) \\ m_3 s^2 X_3(s) + \left( b_3 + b_4 \right) s X_3(s) – b_3 s X_1(s) – b_4 s X_2(s) &=& 0 \end{array} \right. \end{eqnarray} $$
のように、周波数領域sの式に変換することが出来ます。
このラプラス変換に得られた周波数に関する運動方程式を各質量の運動ごとにまとめると
$$ \begin{eqnarray} \left\{ \begin{array}{l} \left[ m_1 s^2 + \left( c_1 + c_2 + b_1 + b_3 \right) s + \left( k_1 + k_2 \right) \right] X_1(s) – \left( c_2 s + k_2 \right) X_2(s) – b_3 s X_3(s) &=& 0 \\ – \left( c_2 s + k_2 \right) X_1(s) + \left[ m_2 s^2 + \left( c_2 + b_2 + b_4 \right) s + k_2 \right] X_2(s) – b_4 s X_3(s) &=& F(s) \\ – b_3 s X_1(s) – b_4 s X_2(s) + \left[ m_3 s^2 + \left( b_3 + b_4 \right) s \right] X_3(s) &=& 0 \end{array} \right. \end{eqnarray} $$
という式が得られます。
このラプラス変換した運動方程式を用いて伝達関数を求めていきます。
伝達関数の算出
入力(力F)に対する出力(各質量の位置X1とX2とX3)の関係を表す伝達関数を求めていきます。
伝達関数を求めるには、先ほどラプラス変換した運動方程式を連立方程式として取り扱います。
各質量の位置X1、X2、X3を力Fで表すことで、伝達関数が求められます。
3つ目の式
$$ – b_3 s X_1(s) – b_4 s X_2(s) + \left[ m_3 s^2 + \left( b_3 + b_4 \right) s \right] X_3(s) = 0 $$
から、位置X3についてX1とX2を用いて
$$ X_3(s) = \frac{b_3 s X_1(s) + b_4 s X_2(s)}{m_3 s^2 + \left( b_3 + b_4 \right) s} $$
の関係式が得られます。
この関係式を、1つ目と2つ目の式
$$ \begin{eqnarray} \left[ m_1 s^2 + \left( c_1 + c_2 + b_1 + b_3 \right) s + \left( k_1 + k_2 \right) \right] X_1(s) – \left( c_2 s + k_2 \right) X_2(s) – b_3 s X_3(s) &=& 0 \\ – \left( c_2 s + k_2 \right) X_1(s) + \left[ m_2 s^2 + \left( c_2 + b_2 + b_4 \right) s + k_2 \right] X_2(s) – b_4 s X_3(s) &=& F(s) \end{eqnarray} $$
に代入すると
$$ \begin{eqnarray} \left[ m_1 s^2 + \left( c_1 + c_2 + b_1 + b_3 \right) s + \left( k_1 + k_2 \right) \right] X_1(s) – \left( c_2 s + k_2 \right) X_2(s) – b_3 s \frac{b_3 s X_1(s) + b_4 s X_2(s)}{m_3 s^2 + \left( b_3 + b_4 \right) s} &=& 0 \\ – \left( c_2 s + k_2 \right) X_1(s) + \left[ m_2 s^2 + \left( c_2 + b_2 + b_4 \right) s + k_2 \right] X_2(s) – b_4 s \frac{b_3 s X_1(s) + b_4 s X_2(s)}{m_3 s^2 + \left( b_3 + b_4 \right) s} &=& F(s) \end{eqnarray} $$
となり、この2式を整理すると
$$ \begin{eqnarray} \left[ \left( m_1 s^2 + \left( c_1 + c_2 + b_1 + b_3 \right) s + \left( k_1 + k_2 \right) \right) \left( m_3 s^2 + \left( b_3 + b_4 \right) s \right) – {b_3}^2 s^2 \right] X_1(s) & \\ – \left[ \left( c_2 s + k_2 \right) \left( m_3 s^2 + \left( b_3 + b_4 \right) s \right) + b_3 b_4 s^2 \right] X_2(s) &= 0 \end{eqnarray} $$
と
$$ \begin{eqnarray} – \left[ \left( c_2 s + k_2 \right) \left( m_3 s^2 + \left( b_3 + b_4 \right) s \right) + b_3 b_4 s^2 \right] X_1(s) & \\ + \left[ \left( m_2 s^2 + \left( c_2 + b_2 + b_4 \right) s + k_2 \right) \left( m_3 s^2 + \left( b_3 + b_4 \right) s \right) – {b_4}^2 s^2 \right] X_2(s) &= F(s) \end{eqnarray} $$
の2つの関係式が得られます。
この2式について連立方程式を解くことにより、位置X1は力Fを用いて
$$ \begin{eqnarray} \left[ \begin{array}{l} \left[ \left( m_1 s^2 + \left( c_1 + c_2 + b_1 + b_3 \right) s + \left( k_1 + k_2 \right) \right) \left( m_3 s^2 + \left( b_3 + b_4 \right) s \right) – {b_3}^2 s^2 \right] \\ \cdot \left[ \left( m_2 s^2 + \left( c_2 + b_2 + b_4 \right) s + k_2 \right) \left( m_3 s^2 + \left( b_3 + b_4 \right) s \right) – {b_4}^2 s^2 \right] \\ – \left[ \left( c_2 s + k_2 \right) \left( m_3 s^2 + \left( b_3 + b_4 \right) s \right) + b_3 b_4 s^2 \right]^2 \end{array} \right] X_1(s) \\ = \left[ \left( c_2 s + k_2 \right) \left( m_3 s^2 + \left( b_3 + b_4 \right) s \right) + b_3 b_4 s^2 \right] F(s) \end{eqnarray} $$
と表されます。
同様に、位置X2は
$$ \begin{eqnarray} \left[ \begin{array}{l} \left[ \left( m_1 s^2 + \left( c_1 + c_2 + b_1 + b_3 \right) s + \left( k_1 + k_2 \right) \right) \left( m_3 s^2 + \left( b_3 + b_4 \right) s \right) – {b_3}^2 s^2 \right] \\ \cdot \left[ \left( m_2 s^2 + \left( c_2 + b_2 + b_4 \right) s + k_2 \right) \left( m_3 s^2 + \left( b_3 + b_4 \right) s \right) – {b_4}^2 s^2 \right] \\ – \left[ \left( c_2 s + k_2 \right) \left( m_3 s^2 + \left( b_3 + b_4 \right) s \right) + b_3 b_4 s^2 \right]^2 \end{array} \right] X_1(s) \\ = \left[ \left( m_1 s^2 + \left( c_1 + c_2 + b_1 + b_3 \right) s + \left( k_1 + k_2 \right) \right) \left( m_3 s^2 + \left( b_3 + b_4 \right) s \right) – {b_3}^2 s^2 \right] F(s) \end{eqnarray} $$
という式が得られます。
ここで、長い式をまとめるために、
$$ \begin{eqnarray} \Delta = \left[ \begin{array}{l} \left[ \left( m_1 s^2 + \left( c_1 + c_2 + b_1 + b_3 \right) s + \left( k_1 + k_2 \right) \right) \left( m_3 s^2 + \left( b_3 + b_4 \right) s \right) – {b_3}^2 s^2 \right] \\ \cdot \left[ \left( m_2 s^2 + \left( c_2 + b_2 + b_4 \right) s + k_2 \right) \left( m_3 s^2 + \left( b_3 + b_4 \right) s \right) – {b_4}^2 s^2 \right] \\ – \left[ \left( c_2 s + k_2 \right) \left( m_3 s^2 + \left( b_3 + b_4 \right) s \right) + b_3 b_4 s^2 \right]^2 \end{array} \right] \end{eqnarray} $$
と置くと、位置X1とX2は
$$ \begin{eqnarray} X_1(s) &=& \frac{ \left( c_2 s + k_2 \right) \left( m_3 s^2 + \left( b_3 + b_4 \right) s \right) + b_3 b_4 s^2 }{\Delta} F(s) \\ X_2(s) &=& \frac{\left( m_1 s^2 + \left( c_1 + c_2 + b_1 + b_3 \right) s + \left( k_1 + k_2 \right) \right) \left( m_3 s^2 + \left( b_3 + b_4 \right) s \right) – {b_3}^2 s^2}{\Delta} F(s) \end{eqnarray} $$
となることが分かりました。
最後に、位置X1とX2に関する式を3つ目の式
$$ \left[ m_3 s^2 + \left( b_3 + b_4 \right) s \right] X_3(s) = b_3 s X_1(s) + b_4 s X_2(s) $$
に代入すると
$$ X_3(s) = \frac{ b_3 s \left( c_2 s + k_2 \right) + b_4 s \left( m_1 s^2 + \left( c_1 + c_2 + b_1 + b_3 \right) s + \left( k_1 + k_2 \right) \right) }{\Delta} F(s) $$
のように位置X3についての式が得られます。
この算出した関係式より、求めたい伝達関数は
$$ \begin{eqnarray} G_1(s) &= \frac{X_1(s)}{F(s)} &= \frac{ \left( c_2 s + k_2 \right) \left( m_3 s^2 + \left( b_3 + b_4 \right) s \right) + b_3 b_4 s^2 }{\Delta} \\ G_2(s) &= \frac{X_2(s)}{F(s)} &= \frac{\left( m_1 s^2 + \left( c_1 + c_2 + b_1 + b_3 \right) s + \left( k_1 + k_2 \right) \right) \left( m_3 s^2 + \left( b_3 + b_4 \right) s \right) – {b_3}^2 s^2}{\Delta} \\ G_3(s) &= \frac{X_3(s)}{F(s)} &= \frac{ b_3 s \left( c_2 s + k_2 \right) + b_4 s \left( m_1 s^2 + \left( c_1 + c_2 + b_1 + b_3 \right) s + \left( k_1 + k_2 \right) \right) }{\Delta} \end{eqnarray} $$
のようになることが分かりました。
まとめ
今回の記事では、3自由度系について運動方程式から伝達関数を求める方法を紹介しました。
取り扱うシステムが複雑になったとしても、一つ一つ確実に求めていくことで、伝達関数を求めることができます。
























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
