本記事は、2自由度振動系で学ぶ制御工学入門の第2回です。
本シリーズでは、2自由度振動系の制御を通して制御工学の基礎知識を学びます。
制御対象システムの運動方程式を求めることは、システムの制御を行う上で重要な第一歩目です。
とても重要な運動方程式ですが、制御対象が2つ以上の質量を含む多自由度系になると数式が複雑になり、運動方程式の導出が難しくなります。
これは、それぞれの質量にかかる力が影響しあい、分かりにくくなるためだと考えられます。
この各質量にかかる力の働きを可視化する方法として、フリーボディダイアグラムがあります。
今回は2自由度系の振動モデルについて、フリーボディダイアグラムにより表した力のつり合いから、運動方程式を求める方法を紹介します。
- 2自由度振動系の運動方程式の導出方法
- フリーボディダイアグラムによる力のつり合いの表現方法
- 各機械要素(質量、ばね、ダンパー)に関する力の算出方法
2自由度振動系モデルの運動方程式
本シリーズでは、シリーズを通して下図に示す2自由度振動系モデルを取り扱っています。
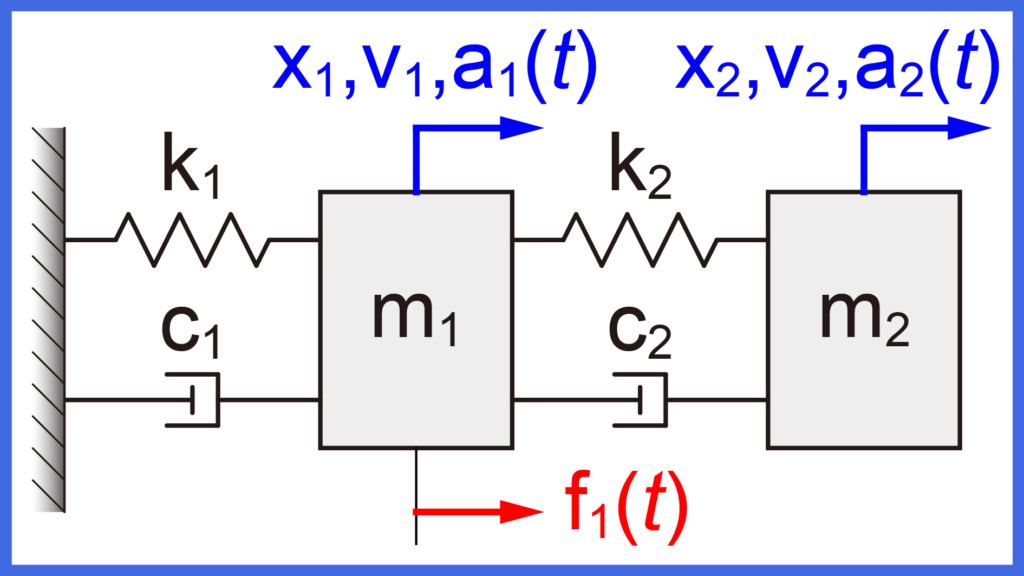
この2自由度系の運動方程式は、以下の式で表されます。
$$ \begin{eqnarray} \left\{ \begin{array}{l} m_1 \ddot{x}_1(t) + \left( c_1 + c_2 \right) \dot{x}_1(t) + \left( k_1 + k_2 \right) x_1(t) – c_2 \dot{x}_2(t) – k_2 x_2(t) &=& f_1(t) \\ m_2 \ddot{x}_2(t) + c_2 \dot{x}_2(t) + k_2 x_2(t) – c_2 \dot{x}_1(t) – k_2 x_1(t) &=& 0 \end{array} \right. \end{eqnarray} $$
本記事では、この2自由度振動系の運動方程式をフリーボディダイアグラムを用いて導出する方法を紹介します。
機械要素により生じる力
機械システムを構成する要素として
- 質量
- ばね
- ダンパー
があります。
ここでは、これら3つの機械要素に関する力について紹介します。
質量
質量に関する力は、質量と加速度の掛け算で表されます。
加速度は質量の時間当たりの速度の変化量で、位置を2回微分することで求められます。
質量mの位置x(t)が与えられた時、質量に関する力Fは
$$ F = m \ddot{x}(t) $$
と表されます。
ばね
ばねにより生じる力は、ばね定数とばね伸び量で表されます。
ばねの伸び量は接続されている質量の位置から求められます。
ばね定数kと変化量x(t)が与えられた時、ばねに関する力Fは
$$ F = k x(t) $$
と表されます。
ダンパー
ダンパーにより生じる力は、ダンパーの減衰係数と速度で表されます。
ダンパーに関する速度は、接続されている質量の速度から求められます。
減衰係数cと位置x(t)が与えられた時、ばねに関する力Fは
$$ F = c \dot{x}(t) $$
と表されます。
これら各機械要素に関する力を用いて、質量にかかる力をフリーボディダイアグラムで表していきます。
フリーボディダイアグラムで表す力の関係
ここでは、フリーボディダイアグラムの基本知識を紹介します。
そして、実際に2自由度振動系についてフリーボディダイアグラムを用いて力の関係を表す方法を説明します。
フリーボディダイアグラムとは
フリーボディダイアグラムとは、対象の物体に与えられる力やモーメント、反力などを可視化した図のことです。
対象の物体に関する力を可視化することで、後に運動方程式などを作成する際に扱いやすくなります。
また、フリーボディダイアグラムを用いることで、複数の質量を含む多自由度システムについても、各質量に関する力を分けて取り扱うことが出来ます。
2自由度振動系のフリーボディダイアグラム
では、本シリーズで取り扱っている2自由度振動系について、実際にフリーボディダイアグラムを使って力の関係を表していきます。
質量m1のフリーボディダイアグラム
まず、質量m1に関するフリーボディダイアグラムを考えます。
質量m1についてのフリーボディダイアグラムは下図のようになります。
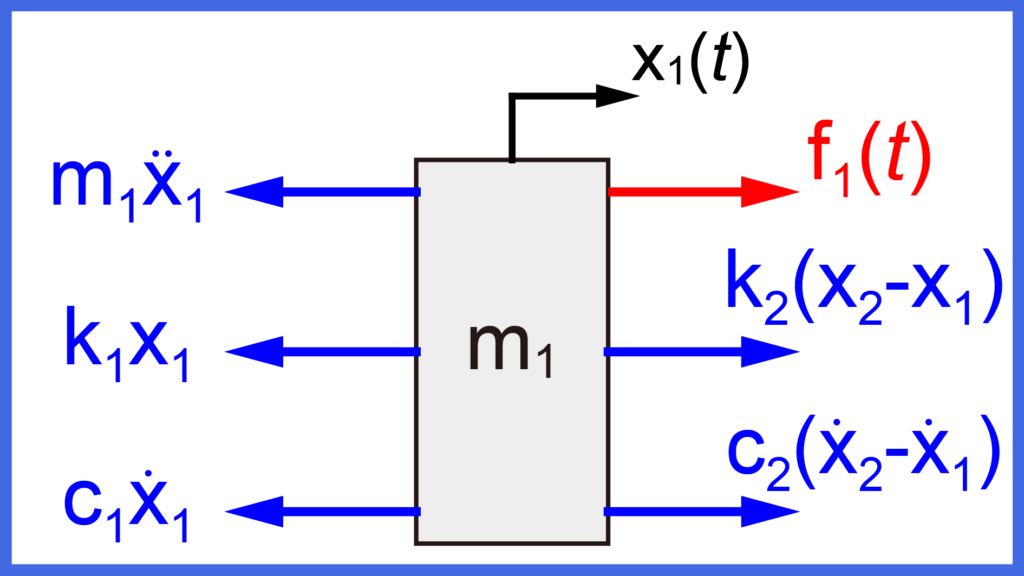
質量m1には外力f1が与えられています。
そして、外力f1と反対方向に質量m1と加速度による力が加わります。
また、質量m1には壁との間にばねk1とダンパーc1、質量m2との間にばねk2とダンパーc2が接続されています。
そのため、これら2組のばねとダンパーの力を考慮する必要があります。
まず、壁側に接続されているばねk1とダンパーc1による力は、質量m1の位置x1や速度v1の向きと反対方向に加わります。
これは、ばねが伸びるほど元に戻ろうとして縮む方向(伸びと反対方向)に力を出すことをイメージすると分かりやすいと思います。
そして、質量m2と接続されているばねk2とダンパーc2による力は、質量m2の位置x2や速度v2と質量m1の位置x1や速度v1との差から求めます。
ばねの力を求める場合、ばねの伸びは質量m2の位置から質量m1の位置を引いた値になります。
同様に、ダンパーにかかる速度は質量m2の速度から質量m1の速度を引くことで求められます。
この時のばねやダンパーによる力は、質量m1の運動方向(位置や速度)と同一方向に加わります。
これらの質量m1に関する力の関係を表したものがフリーボディダイアグラムとなります。
質量m2のフリーボディダイアグラム
次に、質量m2についてのフリーボディダイアグラムを求めると下図になります。
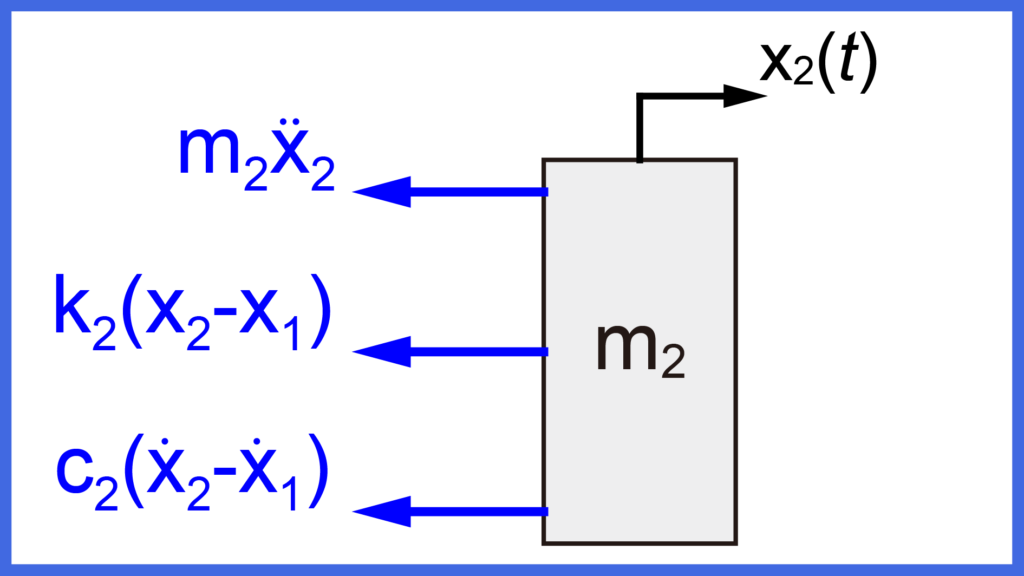
まず、質量m2と加速度a2による力が質量m2の運動と反対方向に加わります。
そして、質量m2には質量m1との間にばねとダンパーが接続されています。
このばねとダンパーによる力は、質量m2の運動と質量m1の運動との差から求められます。
ばねによる力は、質量m2の位置から質量m2の位置を引いた値とばね定数k2から求められます。
同様にダンパーによる力は、質量m2の速度から質量m1の速度を引いた値と減衰係数c2から得られます。
この時、ばねとダンパーによる力は、質量m2の位置や速度の向きと反対方向に加わります。
このように求めたフリーボディダイアグラムから運動方程式を算出します。
2自由度振動系の運動方程式の導出
これまでに求めたフリーボディダイアグラムを用いて、2自由度振動系の運動方程式を求めていきます。
フリーボディダイアグラムにて表された矢印は左向きと右向きとで等しくつり合いの関係になります。
この力の関係を用いて、各質量に関するフリーボディダイアグラムから運動方程式を導出します。
質量m1に関する力の式
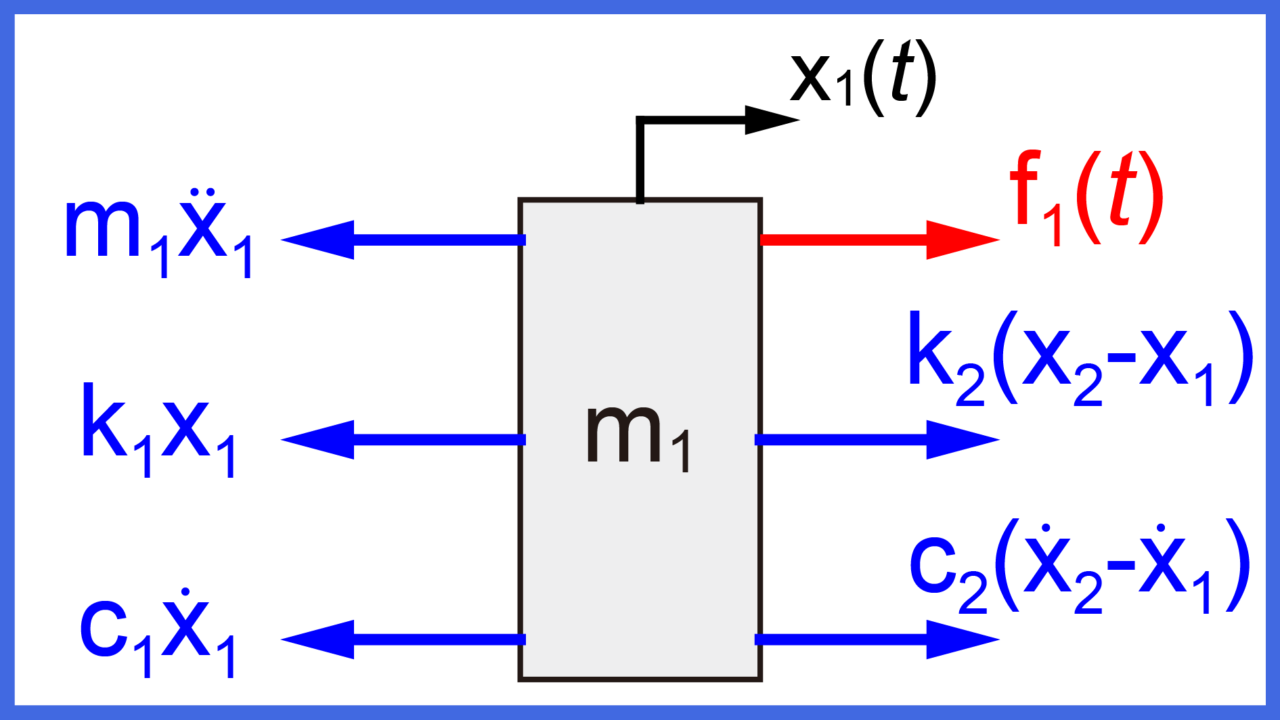
先ほど求めた質量m1についてのフリーボディダイアグラムを下図に示します。

これらフリーボディダイアグラムで表された1つの外力(赤矢印)と5つの力(青矢印)について、矢印の方向ごとにまとめて等式を作ります。
左向き矢印の力を左辺に、右向き矢印の力を右辺として表すと
$$ m_1 \ddot{x}_1(t) + c_1 \dot{x}_1(t) + k_1 x_1(t) = f_1(t) + c_2 \left( \dot{x}_2(t) – \dot{x}_1(t) \right) + k_2 \left( x_2(t) – x_1(t) \right) $$
という等式になります。
この式を整理して、各質量の運動に関する力を左辺に、外力を右辺としてまとめると
$$ m_1 \ddot{x}_1(t) + \left( c_1 + c_2 \right) \dot{x}_1(t) + \left( k_1 + k_2 \right) x_1(t) – c_2 \dot{x}_2(t) – k_2 x_2(t) = f_1(t) $$
となります。
このように求めた数式が、質量m1に関する運動方程式になります。
質量m2に関する力の式
同様に、質量m2についての運動方程式を導出していきます。
先ほど求めた質量m2についてのフリーボディダイアグラムを下図に示します。
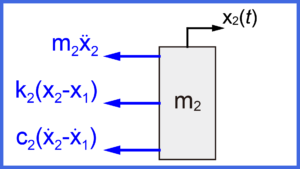
上のフリーボディダイアグラムで表された3つの力(青矢印)について式にまとめます。
質量については外力が無いため、質量のときのような赤矢印はありません。
左向き矢印の力を左辺に、右向き矢印の力はないため0として右辺に表すと
$$ m_2 \ddot{x}_2(t) + c_2 \left( \dot{x}_2(t) – \dot{x}_1(t) \right) + k_2 \left( x_2(t) – x_1(t) \right) = 0 $$
という式になります。
この式について、各質量の運動に関して整理してまとめると
$$ m_2 \ddot{x}_2(t) + c_2 \dot{x}_2(t) + k_2 x_2(t) – c_2 \dot{x}_1(t) – k_2 x_1(t) = 0 $$
と表されます。
このように、質量m2に関する運動方程式を求めることが出来ます。
2自由度振動系の運動方程式
これまでに求めた各質量に関する運動方程式をまとめると、2自由度振動系の運動方程式が得られます。
よって、本シリーズで取り扱っている2自由度系の運動方程式は
$$ \begin{eqnarray} \left\{ \begin{array}{l} m_1 \ddot{x}_1(t) + \left( c_1 + c_2 \right) \dot{x}_1(t) + \left( k_1 + k_2 \right) x_1(t) – c_2 \dot{x}_2(t) – k_2 x_2(t) &=& f_1(t) \\ m_2 \ddot{x}_2(t) + c_2 \dot{x}_2(t) + k_2 x_2(t) – c_2 \dot{x}_1(t) – k_2 x_1(t) &=& 0 \end{array} \right. \end{eqnarray} $$
となることが分かりました。
まとめ
今回の記事では、2自由度系の振動モデルについて、フリーボディダイアグラムにより表した力のつり合いから、運動方程式を求める方法を紹介しました。
今回紹介した手法を用いることで、様々な質量-ばね-ダンパーモデルの運動方程式を求めることが出来ます。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
