前回までの記事では、3次スプライン補間に用いる3次多項式のパラメータを求める方法を紹介しました。
今回と次回の記事では、実際の離散的な指令値を用いて、3次スプライン補間で連続的な軌跡を作成していきます。
3次多項式のパラメータの関係式
離散点\(x_i\)と\(x_{i+1}\)の間を補間する3次多項式\(S_i\)
$$ S_i(x) = a_i + b_i (x-x_i) + c_i (x-x_i)^2 + d_i (x-x_i)^3 $$
について、3次スプライン補間の条件
- 条件１：各区間の始点
- 条件２：位置の連続性
- 条件３：速度の連続性
- 条件４：加速度の連続性
- 条件５：軌跡の始点と終点
より、3次多項式のパラメータ（\(a_i, b_i, c_i, d_i\)）について
$$ a_i = y_i $$
$$ h_{i+1} c_{i+2} + 2 (h_{i+1} + h_i) c_{i+1}+ c_i h_i = \frac{3}{h_{i+1}}(a_{i+2}-a_{i+1}) – \frac{3}{h_i}(a_{i+1}-a_i) $$
$$ b_i = \frac{a_{i+1}-a_i}{h_i} – \frac{h_i(c_{i+1}+2 c_i)}{3} $$
$$ d_i = \frac{c_{i+1}-c_i}{3 h_i} $$
の関係が成り立ちます。
離散点から３次多項式のパラメータを算出
3次スプライン補間の条件より導かれた各パラメータの関係式を用いて、実際にX-Y平面上に表された離散的な指令点を連続的に補間していきます。
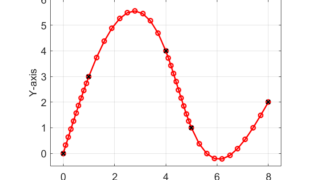
今回の記事で補間する離散的な指令点は下記のように定義します。
$$ \begin{eqnarray} \begin{array}{c|c} X-axis & Y-axis \\ \hline 0 & 0 \\ 1 & 3 \\ 4 & 4 \\ 5 & 1 \\ 8 & 2 \\ \end{array} \end{eqnarray} $$
この離散的に与えられた指令点について、入力をX軸、出力をY軸として3次スプライン補間を用いて連続的で滑らかな経路を生成します。
パラメータ\(a_i\)を求める
3次多項式に含まれるパラメータ\(a_i\)を求めていきます。
前回求めたパラメータ\(a_i\)に関する関係式より、パラメータ\(a_i\)は出力\(y_i\)と同値になります。
よって、3次多項式のパラメータ\(a_i\)は、
$$ a_0 = y_0 = 0 $$
$$ a_1 = y_1= 3 $$
$$ a_2 = y_2= 4 $$
$$ a_3 = y_3= 1 $$
$$ a_4 = y_4= 2 $$
と求めることが出来ます。
各区間の変化量\(h_i\)を求める
ここで、他のパラメータ（\(b_i\)、\(c_i\)、\(d_i\)）を求める際に必要となる、各区間における入力\(x\)の変化量\(h_i\)を求めておきます。
離散点\(x_i\)と\(x_{i+1}\)の間の区間における入力\(x\)の変化量\(h_i\)は
$$ h_i = x_{i+1} – x_i $$
で求めることが出来ます。
よって、各区間における入力の変化量は
$$ h_0 = 1-0=1 $$
$$ h_1 = 4-1=3 $$
$$ h_2 = 5-4=1 $$
$$ h_3 = 8-5=3 $$
となります。
パラメータ\(c_i\)を求める
先程求めたパラメータ\(a_i\)と変化量\(h_i\)から３次多項式のパラメータ\(c_i\)を求めていきます。
前回求めたパラメータ\(c_i\)と\(a_i\)の関係式より、以下の行列式を作成します。
$$ A \cdot c = b $$
ここで、行列\(A\)とベクトル\(c\)と\(b\)は
$$ A = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 1 & 8 & 3 & 0 & 0 \\ 0 & 3 & 8 & 1 & 0 \\ 0 & 0 & 1 & 8 & 3 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix} $$
$$ c = \begin{bmatrix} c_0 \\ c_1 \\ c_2 \\ c_3 \\ c_4 \end{bmatrix} $$
$$ b = \begin{bmatrix} 0 \\ \frac{3}{3}(4-3) – \frac{3}{1}(3-0) \\ \frac{3}{1}(1-4) – \frac{3}{3}(4-3) \\ \frac{3}{3}(2-1) – \frac{3}{1}(1-4) \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ -8 \\ -10 \\ 10 \\ 0 \end{bmatrix} $$
とパラメータ\(a_i\)と変化量\(h_i\)から求めることが出来ます。
また、3次スプライン補間の条件より、
$$ c_0 = 0 $$
$$ c_4 = 0 $$
が導かれます。
この行列式より以下の連立方程式を導くことが出来ます。
$$ 8 c_1 + 3 c_2 = -8 $$
$$ 3 c_1 + 8 c_2 + c_3 = -10 $$
$$ c_2 + 8 c_3 = 10 $$
この連立方程式を解くことで、3次多項式のパラメータ\(c_i\)を求めます。
1つ目の式から、パラメータ\(c_1\)は\(c_2\)を用いて
$$ 8 c_1 + 3 c_2 = -8 $$
$$ \Rightarrow c_1 = \frac{-3 c_2 – 8}{8} $$
と表すことが出来ます。
同様に3つ目の式から、パラメータ\(c_3\)は\(c_2\)を用いて
$$ c_2 + 8 c_3 = 10 $$
$$ \Rightarrow c_3 = \frac{-c_2 + 10}{8} $$
と表されます。
このパラメータ\(c_1\)と\(c_3\)について2式を2つ目の式に代入することで、パラメータ\(c_2\)を求めていきます。
$$ 3 c_1 + 8 c_2 + c_3 = -10 $$
$$ \Rightarrow 3 \frac{-3 c_2 – 8}{8} + 8 c_2 + \frac{-c_2 + 10}{8} = -10 $$
$$ \Rightarrow -9 c_2 – 24 + 64 c_2 – c_2 + 10 = -80 $$
$$ \Rightarrow 54 c_2 = -66 $$
$$ \Rightarrow c_2 = \frac{-11}{9} = -1.2222 $$
求めたパラメータ\(c_2\)を用いて、パラメータ\(c_1\)と\(c_3\)を先に求めた式に\(c_2\)の値を代入して求めていきます。
$$ c_1 = \frac{-3 c_2 – 8}{8} $$
$$ \Rightarrow c_1 = \frac{-3 \frac{-11}{9} – 8}{8} = \frac{-13}{24} = -0.5417 $$
$$ c_3 = \frac{-c_2 + 10}{8} $$
$$ \Rightarrow c_3 = \frac{-\frac{-11}{9} + 10}{8} = \frac{101}{72} = 1.4028 $$
以上のように、3次多項式のパラメータ\(c_i\)を求めることが出来ました。
逆行列を用いてパラメータ\(c_i\)を求める
3次多項式のパラメータ\(c_i\)について、パラメータ\(a_i\)との関係式から導いた行列式から、逆行列を用いて算出することも出来ます。
パラメータ\(c_i\)とパラメータ\(a_i\)との関係式より求められる行列式
$$ A c = b $$
について、両辺の左側から行列\(A\)の逆行列\(A^{-1}\)を掛けることで
$$ A c = b $$
$$ \Rightarrow A^{-1}A c = A^{-1} b $$
$$ \Rightarrow c = A^{-1} b $$
と、パラメータ\(c_i\)を示すベクトルを行列\(A\)の逆行列\(A^{-1}\)と行列\(b\)から求めることが出来ます。
実際に先程の逆行列を用いた行列式からパラメータ\(c_i\)を求めると
$$ c_0 = 0 $$
$$ c_1 = -0.5417 $$
$$ c_2 = -1.2222 $$
$$ c_3 = 1.4028 $$
$$ c_4 = 0 $$
となります。
これらパラメータ\(c_i\)の値は、連立方程式を用いて算出された値と同じになります。
まとめ
今回は、実際の離散的な指令値を用いて、3次スプライン補間による連続的で滑らかな軌跡を作成する方法を紹介しました。
3次スプライン補間の条件より導かれた3次多項式のパラメータの関係式より、本記事ではパラメータ\(a_i\)と\(c_i\)を算出しました。
次回は、残りのパラメータ\(b_i\)と\(d_i\)を算出して、3次多項式を用いた3次スプライン補間による軌跡生成を行っていきたいと思います。
ELEGOO Arduinoスターターキット
UNO R3スマートロボットカー
Raspberry Pi 3 Model b+
