車輪ロボット（対向2輪型）の運動を計算してみよう

今回は車輪ロボットとして対向2輪型ロボットの運動を取り扱いたいと思います。

車輪ロボットの中でもシンプルな構造なので、移動ロボットの運動を理解するには良いと思います。

対向2輪型ロボットの構造

対向2輪型の車輪ロボットは、2つの車輪が車体を挟んで向かい合って設置されたモデルです。

構造がシンプルなので、作成するのが簡単です。

ロボットの運動を計算する際も、シンプルに数式で表すことが出来ます。

また、自動車とは異なり、その場で旋回することもできるため、制御する際の自由度が高いといった利点もあります。

対向2輪型ロボットの運動

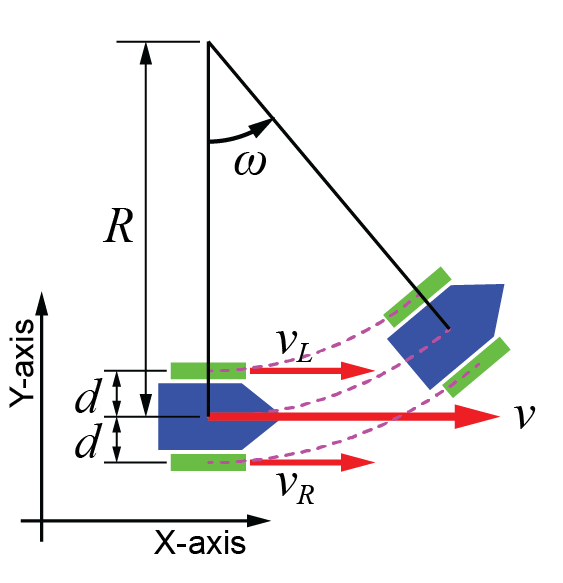
実際に対向2輪型移動ロボットの運動を計算していきます。

ロボットの移動速度\( v \)は、旋回角速度\( \omega \)と旋回半径\( R \)を用いて

$$ v = R\omega $$

となります。

移動速度\( v \)と同様に、各車輪の速度（\( v_R \)と\( v_L \)）を旋回角速度\( \omega \)と旋回半径\( R \)、車輪と車体中心までの距離\( d \)を用いて表すと

$$ v_R = (R+d)\omega $$

$$ v_L = (R-d)\omega $$

となります。

これらの式を解くと、移動ロボットの移動速度\( v \)と旋回角速度\( \omega \)、旋回半径\( R \)は、各車輪の速度（\( v_R \)と\( v_L \)）と車輪と車体中心までの距離\( d \)を用いて下記のように表すことが出来ます。

$$ v = (v_R+v_L)/2 $$

$$ \omega = (v_R-v_L)/2d $$

$$ R = v/\omega = d(v_R+v_L)/(v_R-v_L) $$

この関係式はロボットの動きをロボット自身の座標系で見た値です。

これを基準の座標系（\( [x,y,\theta] \)）で表した場合は

$$ \dot{x} = v \cos(\theta) $$

$$ \dot{y} = v \sin(\theta) $$

$$ \dot{\theta} = \omega $$

となります。

対向2輪型ロボットの位置

次に、計算した運動を表す式を用いて移動ロボットの位置を計算していきます。

時刻\( t+1 \)での対向2輪型ロボットの移動は、現在の時刻\( t \)におけるロボット位置（\( [x_t,y_t,\theta_t] \)）と先ほど求めた運動の式（\( \dot{x},\dot{y},\dot{\theta} \)）、現在の時刻\( t \)と求める時刻\( t+1 \)との差\( \Delta t \)で表すことが出来ます。

$$ x_{t+1} = x_t + \dot{x}\Delta t \cos(\theta_t + \dot{\theta}\Delta t/2) $$

$$ y_{t+1} = y_t + \dot{y}\Delta t \sin(\theta_t + \dot{\theta}\Delta t/2) $$

$$ \theta_{t+1} = \theta_t + \dot{\theta}\Delta t  $$

まとめ

今回は、車輪移動ロボットとして、対向2輪型モデルを例にとりロボットの運動と移動を式で表してみました。

この式を用いることで、対向2輪型ロボットを用いた様々な制御を行うことが可能になります。