根軌跡を描くことが出来れば、複雑なフィードバックシステムの挙動を簡単に理解することが出来ます。
前回までの記事では、根軌跡を描くために必要なルールと描き方を紹介しました。
今回の記事では、詳細な根軌跡を描くために必要となる情報について紹介していきたいと思います。
詳細な根軌跡を描くための情報
より詳細な根軌跡を書くために必要となる情報として、
- 実軸上からの分岐点 ← 今回
- 虚軸との交点
- 複素数点への入出力角
があります。
今回は、1つ目の実軸上から分岐する点を求める方法を紹介します。
フィードバックシステムと実軸上からの分岐点
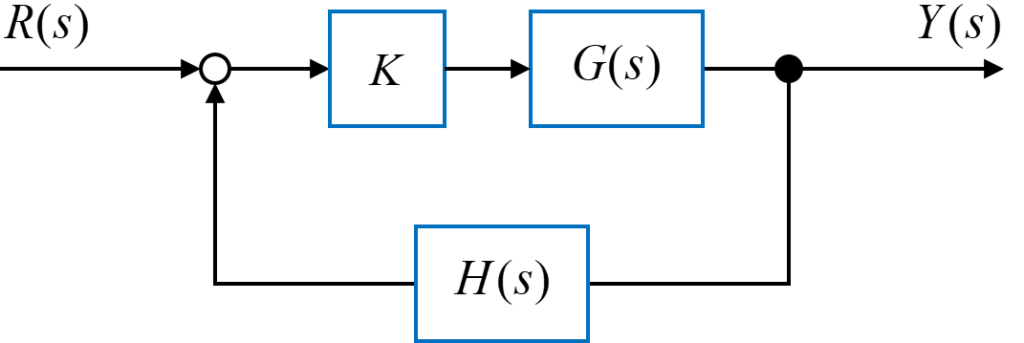
図のようなフィードバックシステムの開ループ伝達関数が
$$ K G(s) H(s) = \frac{K (s+1)(s+2)}{(s+3)(s+4)} $$
が与えられたシステムについての根軌跡を考えます。
前回までの記事で紹介した根軌跡のルールを用いることで、今回のフィードバックシステムの根軌跡の概略を描くことが出来ます。
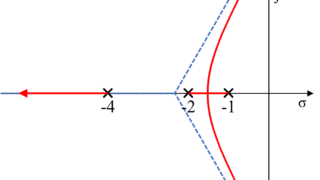
開ループ伝達関数の極\(-3\)と\(-4\)を始点とした軌跡が実軸上で合わさり、ある点で上下方向に分岐されます。
そのあと円弧のような形を描いたのちに、ある点で実軸上で交わった後に開ループ伝達関数の零点\(-1\)と\(-2\)に向かいます。
この実軸上から分岐する点を求めていきます。
実軸上からの分岐点を算出する
根軌跡の基本的なルールより、閉ループ伝達関数の極の位置はゲイン\(K\)を大きくするごとに開ループ伝達関数の極から零点に向けて移動していきます。
これより、開ループ伝達関数の極\(-3\)と\(-4\)が合わさり、実軸上から分岐していく点でのゲイン\(K\)は、\(-3\)と\(-4\)の間で最大となります。
また、実軸上に合流した後に開ループ伝達関数の零点\(-1\)と\(-2\)に向かう点でのゲイン\(K\)は、\(-1\)と\(-2\)の間で最小になります。
さらに、開ループ伝達関数と根軌跡上の点の特徴から
$$ K G(s) H(s) = -1 $$
が成り立ちます。
これらの関係式を用いて、ゲイン\(K\)についての式を算出し、微分したのちに変化点を算出することでゲイン\(K\)が最大または最小になる点を求めます。
実際に分岐点を算出する
紹介した方法を用いて、根軌跡の実軸上からの分岐点を算出していきます。
今回用いているフィードバックシステムの開ループ伝達関数は
$$ K G(s) H(s) = \frac{K (s+1)(s+2)}{(s+3)(s+4)} $$
です。
また、根軌跡上の点の特徴から
$$ K G(s) H(s) = -1 $$
より、開ループ伝達関数は
$$ \frac{K (s+1)(s+2)}{(s+3)(s+4)} = -1 $$
$$ \Rightarrow K = \frac{-(s^2+7s+12)}{s^2+3s+2} $$
という関係式が成り立ちます。
ここで
$$ s = \sigma $$
として、分岐点\(\sigma\)を求めます。
ゲイン\(K\)についての式を分岐点\(\sigma\)で微分すると、
$$ \frac{d K}{d \sigma} = \frac{-(2 \sigma +7)({\sigma}^2+3 \sigma +2)+({\sigma}^2+7 \sigma +12)(2 \sigma +3)}{({\sigma}^2+3 \sigma +2)^2} = 0 $$
$$ \frac{4 {\sigma}^2 + 20 \sigma + 22}{({\sigma}^2+3 \sigma +2)^2} = 0 $$
となります。
よって、この式を分岐点\(\sigma\)について解くと
$$ 4 {\sigma}^2 + 20 \sigma + 22 = 0 $$
$$ \Rightarrow \sigma = -3.366, -1.634 $$
となります。
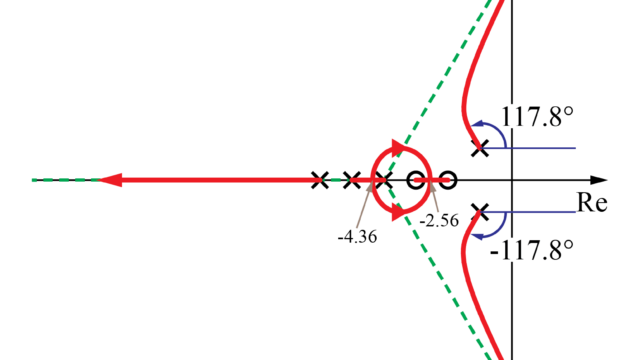
これより、開ループ伝達関数の極\(-3\)と\(-4\)を始点とした軌跡は分岐点\(\sigma = -3.366\)で実軸上から分岐することが分かります。
そして、開ループ伝達関数の零点\(-1\)と\(-2\)を終点とする軌跡は流入点\(\sigma = -1.634\)で実軸上に流入することが分かりました。
まとめ
今回は、詳細な根軌跡を描くために必要となる実軸上からの分岐点の求め方について紹介しました。
次回は、より詳細な根軌跡を書くために軌跡と虚軸との交点を求める方法を紹介したいと思います。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
