ロボットなどを動かす経路を指定する際に、通過してほしい点を離散的な指令点で指示することが多くあります。
この様な離散的な点を指令として与えられた場合、実際にロボットの軌跡を望む通りに制御するためには、連続的なロボットの経路を作成する必要があります。
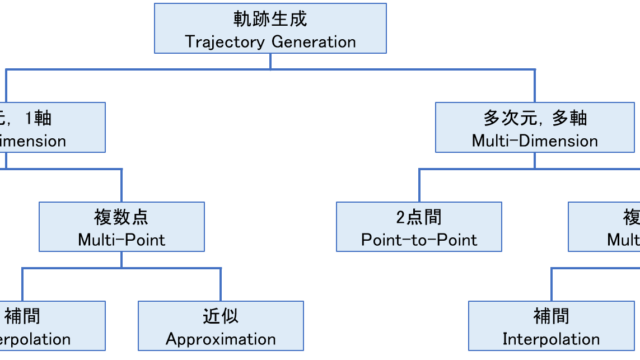
今回からの記事では、離散的な指令点から連続的な軌跡を生成する方法として、3次スプライン補間と呼ばれる3次多項式を用いた離散点を補間する方法を紹介していきます。
3次スプライン補間とは
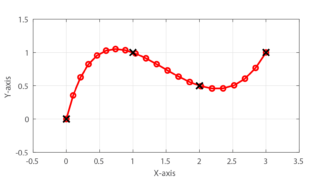
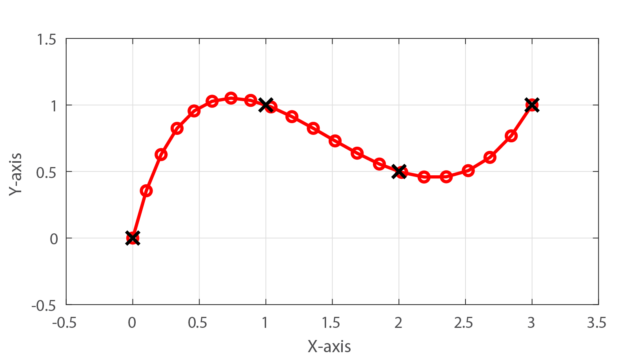
3次スプライン補間とは、離散的な指令点が与えられた場合に、その離散点間を3次の多項式で補間し、滑らかな経路を作成する方法です。
3次スプライン補間は、複雑な計算がなく、加速度(位置の2階微分)の連続性が保たれているため、広く一般的に用いられています。
各離散点(\(x_i\)と\(x_{i+1}\))の間を補間する3次多項式は
$$ S_i(x) = a_i + b_i (x-x_i) + c_i (x-x_i)^2 + d_i (x-x_i)^3 $$
で表されます。
この時、変数\(x\)の取りうる範囲は
$$ x = [x_i, x_{i+1}] $$
です。
この各離散点を補間する3次多項式に含まれるパラメータ
$$ a_i, b_i, c_i, d_i $$
を各範囲において求めることで、滑らかな経路を作成します。
3次スプライン補間の条件
各離散点を補間するパラメータ(\(a_i, b_i, c_i, d_i\))を決定するために、3次スプライン補間の条件を定義します。
今回は、入力を\(x\)、出力を\(y\)として3次多項式を用いた離散点の補間について考えていきます。
条件1:各区間の始点
離散点\(x_i\)と\(x_{i+1}\)の区間を3次多項式を用いて補間された経路において、変数\(x\)が区間の始点\(x_i\)の時には
$$ S_i(x_i) = y_i $$
と、3次多項式の値は\(y_i\)になります。
条件2:位置の連続性
離散点\(x_i\)と\(x_{i+1}\)を3次多項式を用いて補間された経路において、変数\(x\)が終点\(x_{i+1}\)の時には
$$ S_i(x_{i+1}) = y_{i+1} $$
と、3次多項式の値は\(y_{i+1}\)になります。
また、先ほどの条件1でも示したように、次の離散点\(x_{i+1}\)と\(x_{i+2}\)の区間を補間した経路について、変数\(x\)が始点\(x_{i+1}\)の時には
$$ S_{i+1}(x_{i+1}) = y_{i+1} $$
となります。
よって、
$$ S_i(x_{i+1}) = S_{i+1}(x_{i+1}) = y_{i+1} $$
の関係式が導かれます。
このように各区間の境界での条件として、各区間の位置は必ず連続する必要があります。
条件3:速度の連続性
条件2で示した位置の連続性に加えて、各区間の境界では速度も連続する必要があります。
離散点を補間する3次多項式の微分を
$$ \frac{d S_i(x)}{d x} = S_i'(x) $$
と表します。
この時、各区間の境界条件として速度が連続するためには、
$$ S_i'(x_{i+1}) = S_{i+1}'(x_{i+1}) $$
が成り立つ必要があります。
条件4:加速度の連続性
条件2の位置、条件3の速度と同様に、各区間の境界では加速度も連続することで、滑らかの連続した経路を作成することが出来ます。
離散点を補間する3次多項式の2階微分を
$$ \frac{d^2 S_i(x)}{d x^2} = S_i^{(2)}(x) $$
で表した時、各区間の境界条件として加速度が連続するためには、
$$ S_i^{(2)}(x_{i+1}) = S_{i+1}^{(2)}(x_{i+1}) $$
が条件として導かれます。
条件5:軌跡の始点と終点
離散点で与えられた指令点の始点と終点について、
$$ S_0^{(2)}(0) = S_{end-1}^{(2)}(x_{end}) = 0 $$
と、加速度を0に設定します。
このような始点と終点の加速度についての条件を用いた補間手法を自然3次スプライン補間と言います。
まとめ
今回は、離散的に与えられたロボットなどの制御指令を連続的にするための方法として、3次スプライン補間を紹介しました。
また、3次スプライン補間に用いる3次多項式について、各パラメータを決定するための条件についても紹介しました。
3次多項式を用いることで、離散的な点を連続的で滑らかな経路を作成することが出来ます。
次回は、今回紹介した3次スプライン補間の条件を基に、3次多項式の各パラメータを求める方法を紹介していきたいと思います。

合わせて読みたい
5次スプライン曲線を用いた離散点補間についてはこちら

3次スプラインによる離散点の曲線近似はこちら
























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
