ロボットや工作機械などのシステムの伝達関数が与えられた場合に、ボード線図を書く方法を紹介します。
前回までの記事では、伝達関数を構成する要素ごとにボード線図を書く方法を紹介してきました。

今回からは、実際にシステム全体の伝達関数からボード線図を書く方法を紹介していきます。
システムの伝達関数と構成要素
取り扱う伝達関数
今回は、伝達関数\(G(s)\)として
$$ G(s) = \frac{4(s+5)}{s (s+0.2) (s+10)} $$
を取り扱います。
この伝達関数\(G(s)\)について、伝達関数を構成する要素ごとに分割することで、実際に全体のボード線図を書いていきます。
伝達関数を要素ごとに分割
伝達関数\(G(s)\)について、
$$ \begin{eqnarray} G(s) &=& \frac{4(s+5)}{s (s+0.2) (s+10)} \\ &=& 4 \cdot (s+5) \cdot \frac{1}{s} \cdot \frac{1}{s+0.2} \cdot \frac{1}{s+10} \end{eqnarray}$$
と要素ごとに分割することが出来ます。
分割した結果より、今回の伝達関数\(G(s)\)の場合は、
- 比例要素:\(4\)
- 積分要素:\(\frac{1}{s}\)
- 1次進み要素:\(s+5\)
- 1次遅れ要素:\(\frac{1}{s+0.2}\)、\(\frac{1}{s+10}\)
から構成されていることが分かります。
この分割した要素ごとにボード線図を求め、それらを足し合わせることで全体のボード線図を書くことが出来ます。
各要素のボード線図を書きやすくする方法
要素ごとのボード線図を書く前に、各要素ごとのボード線図を足し合わせを容易にするための方法を紹介します。
1次進み要素のボード線図
今回の伝達関数\(G(s)\)に含まれている1次進み要素の\(s+5\)に注目します。
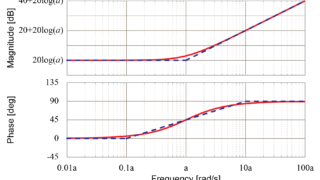
この1次進み要素\(s+5\)について、低周波数領域でのゲイン線図の値は
$$ 20 \log 5 = 13.98 [dB] $$
になります。
そして、周波数\(\omega\)が\(\omega=5\)の地点を境に-20 [dB/decade]で減少します。
このボード線図について、各要素ごとのボード線図を足し合わせる際に、13.98 [dB]のような低周波領域での値をもつゲイン線図を足し合わせることは、計算が複雑になってしまいます。
1次進み要素を変換する
そこで、この1次進み要素について、
$$ s+5 \Rightarrow 5 (\frac{s}{5}+1) $$
のように変換することで、後々ボード線図の足し合わせが容易にすることが出来ます。
このように変換することで、1次進み要素\(s+5\)は、比例要素の\(5\)と1次進み要素の\(\frac{s}{5}+1\)に分けて考えることが出来ます。
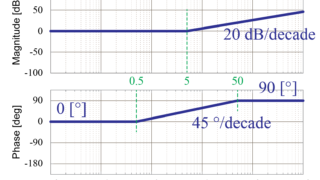
変換された1次進み要素\(\frac{s}{5}+1\)について、低周波数領域でのゲイン線図の値は
$$ 20 \log 1 = 0 [dB] $$
となります。
こうすることで、先ほどの方法では考慮する必要があった低周波数領域でのゲインの値がなくなり(0dBのため)、ゲイン線図の足し合わせがとても容易になります。
また残された比例要素\(5\)は、元の伝達関数内に含まれる比例要素と合わせることで、容易にボード線図を求めることが出来ます。
伝達関数を変換する
ボード線図の足し合わせを容易にするために、与えられた伝達関数\(G(s)\)を変換します。
先程紹介したように、伝達関数\(G(s)\)に含まれる1次進み要素\(s+5\)は
$$ s+5 \Rightarrow 5 (\frac{s}{5}+1) $$
と変換します。
また、伝達関数\(G(s)\)に含まれる2つの1次遅れ要素についても
$$ s+0.2 \Rightarrow \frac{1}{5} (5 s + 1) $$
$$ s+10 \Rightarrow 10 (\frac{s}{10}+1) $$
と変換することが出来ます。
これより、与えられた伝達関数\(G(s)\)は
$$ \begin{eqnarray} G(s) &=& \frac{4 \cdot 5 (\frac{s}{5}+1)}{s \cdot \frac{1}{5} (5 s+1) \cdot 10(\frac{s}{10}+1)} \\ &=& \frac{10 (\frac{s}{5}+1)}{s (5 s+1) (\frac{s}{10}+1)} \end{eqnarray} $$
となります。
よって、今回の伝達関数\(G(s)\)のボード線図を求めるためには、
- 比例要素:\(10\)
- 積分要素:\(\frac{1}{s}\)
- 1次進み要素:\(\frac{s}{5}+1\)
- 1次遅れ要素:\(\frac{1}{5s+1}\)、\(\frac{1}{\frac{s}{10}+1}\)
の各要素についてボード線図を求めて、それらを足し合わせればよいことが分かりました。
この様に伝達関数\(G(s)\)を書き換えることで、後々各要素ごとに求めたボード線図を足し和わせる際に、計算を容易にすることが出来ます。
まとめ
今回は、システムの伝達関数からボード線図を書くために、伝達関数を要素ごとに分割し、変換する方法を紹介しました。
紹介した方法を用いることで、各要素ごとのボード線図を求めた後の足し合わせを容易にすることが出来ます。
次回からは、引き続き伝達関数からボード線図を書くために、各要素ごとにボード線図を求め、それらを足し合わせることで全体のボード線図を求めていきたいと思います。
























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
