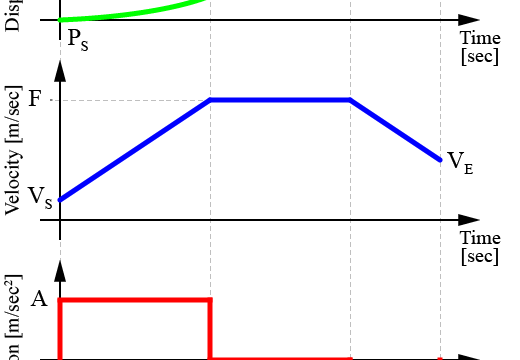
加速度制限による台形速度制御を行うことで、ロボットや機械を滑らかに動作させることが出来ます。
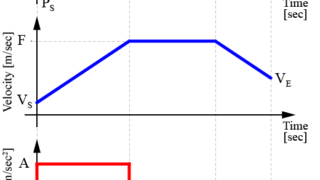
以前の記事では、この加速度制限により生成した台形速度の軌跡について、量子化を行うことで正確な制御を実現する方法を紹介しました。

今回の記事では、実際に具体的な値を用いて軌跡生成を行い、量子化を用いた加速度制限による速度プロファイルの作成方法を紹介します。
取り扱う軌跡生成の条件
今回の記事で生成する軌跡の条件として、移動距離L、最大速度F、最大加速度Aはそれぞれ
$$ \begin{eqnarray} \left\{ \begin{array}{l} L = 10 \ [m] \\ F = 5 \ [m/sec] \\ A = 4 \ [m/{sec}^2] \end{array} \right. \end{eqnarray} $$
と定義します。
また、初速VSと終速VEはそれぞれ
$$ \begin{eqnarray} \left\{ \begin{array}{l} V_S = 0 \ [m/sec] \\ V_E = 2 \ [m/sec] \end{array} \right. \end{eqnarray} $$
として、軌跡を生成します。
そして、制御の際に考慮する必要があるサンプリング時間Tsは
$$ T_s = 0.1 \ [sec] $$
として、軌跡の量子化を行います。
これらの条件をもとに、サンプリング時間を考慮せずに台形速度の軌跡生成を行った結果はこちらの記事で紹介しました。
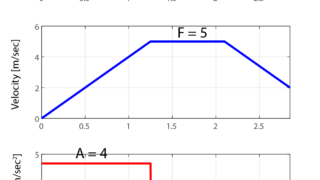
今回は、実際に生成した軌跡を使って制御するために、サンプリング時間に合わせて軌跡の量子化を行いたいと思います。
パラメータの算出
与えられた条件
- 移動距離:L
- 最大速度:V
- 最大加速度:A
- 初速:VS
- 終速:VE
より、台形速度プロファイルの軌跡生成に必要なパラメータ
- 加速期間:T1
- 巡航期間:T2
- 減速期間:T3
を求めます。

加速期間T1と減速期間T3を求める
最大速度Vと最大加速度A、そして初速VSと終速VEより、加速期間T1と減速期間T3を求めると
$$ \begin{eqnarray} T_1 &=& \frac{F – V_S}{A} &=& 1.25 \ [sec] \\ T_3 &=& \frac{F – V_E}{A} &=& 0.75 \ [sec] \end{eqnarray} $$
となります。
巡航期間T2を求める
巡航期間T2を求めるために、まず加速期間T1と減速期間T3で移動する距離L1とL3を求めると
$$ \begin{eqnarray} L_1 &=& \frac{\left( F + V_S \right) T_1}{2} &=& 3.125 \ [m] \\ L_3 &=& \frac{\left( F + V_E \right) T_3}{2} &=& 2.625 \ [m] \end{eqnarray} $$
となります。
この各期間での移動距離L1とL3と全体の移動距離Lより、巡航期間T2は
$$ T_2 = \frac{L – L_1 – L_3}{F} = 0.85 \ [sec] $$
と求めることが出来ます。

巡航期間T2の有無を確認する
与えられた軌跡の条件によっては、巡航期間T2が存在しない場合があるため、その巡航期間T2の有無を確認する必要があります。
今回の条件では、巡航期間T2を求めた結果は0.85secなので、巡航期間は存在します。
このように巡航期間T2が存在する場合は、算出した加速期間T1、巡航期間T2、減速期間T3の値は変更する必要はありません。
また、条件で与えられた最大速度Fと加最大速度Aはそのまま用いることが出来ます。
もし、巡航期間T2が存在しない場合は、こちらの記事で紹介したように各期間(T1とT3)や最大速度Fを巡航期間T2を用いない手法で算出しなおす必要があります。
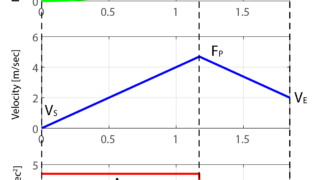
パラメータの量子化
算出した台形速度プロファイルの軌跡生成に必要なパラメータ
- 加速期間:T1
- 巡航期間:T2
- 減速期間:T3
について、量子化を行うことでサンプリング時間Tsの整数倍し、他のパラメータ
- 巡航速度:V
- 加速時の加速度:A1
- 減速時の加速度:A3
の調整を行います。
各期間を量子化する
まず初めに、天井関数を用いて各期間の時間(T1、T2、T3)をサンプリング時間(Ts=0.1 [sec])の何倍にするべきかを求めると
$$ \begin{eqnarray} \left\{ \begin{array}{l} N_1 &=& \lceil \frac{T_1}{T_s} \rceil = \lceil \frac{1.25}{0.1} \rceil = \lceil 12.5 \rceil &=& 13 \\ N_2 &=& \lceil \frac{T_2}{T_s} \rceil = \lceil \frac{0.85}{0.1} \rceil = \lceil 8.5 \rceil &=& 9 \\ N_3 &=& \lceil \frac{T_3}{T_s} \rceil = \lceil \frac{0.75}{0.1} \rceil = \lceil 7.5 \rceil &=& 8 \end{array} \right. \end{eqnarray} $$
となります。
求めたNiより、量子化後の各期間の値は
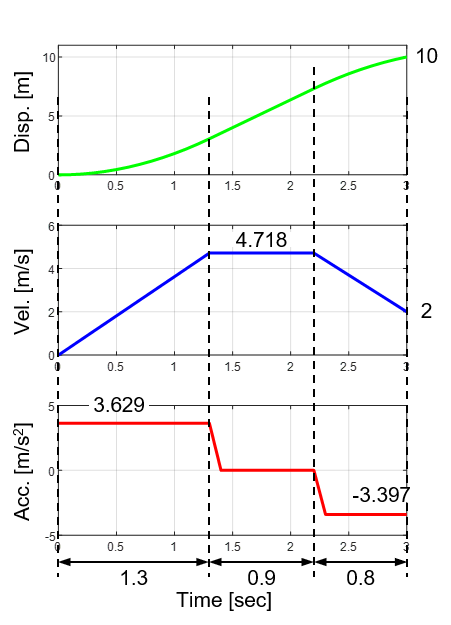
$$ \begin{eqnarray} \left\{ \begin{array}{l} T_1 &=& N_1 T_s = 13 \cdot 0.1 &=& 1.3 \ [sec] \\ T_2 &=& N_2 T_s = 9 \cdot 0.1 &=& 0.9 \ [sec] \\ T_3 &=& N_3 T_s = 8 \cdot 0.1 &=& 0.8 \ [sec] \end{array} \right. \end{eqnarray} $$
となる事が分かりました。
速度と加速度の調整
サンプリング時間Tsに合わせて量子化を行うことで、各期間(T1、T2、T3)の値は大きくなります。
そのため、量子化した各期間の値(T1、T2、T3)に合わせて、速度Vと加速度Aの値を調整する必要があります。
まず、巡航期間T2での速度Vは
$$ \begin{eqnarray} V &=& \frac{2 L – V_S T_1 – V_E T_3}{T_1 + 2 T_2 + T_3} \\ &=& \frac{2 \cdot 10 – 0 \cdot 1.3 – 2 \cdot 0.8}{1.3 + 2 \cdot 0.9 + 0.8} \\ &=& 4.718 \ [m/sec] \end{eqnarray} $$
となります。
この調整後の速度Vは与えられた最大速度Fよりも小さい値になります。
これは、量子化により制御期間(移動期間、T1+T2+T3)が伸びたため、移動距離Lを守るためには速度を下げる必要があるためです。
つぎに変更した速度Vを用いて、加速期間T1と減速期間T3の加速度(A1とA3)を変更すると
$$ \begin{eqnarray} A_1 &=& \frac{F – V_S}{T_1} = \frac{4.718 – 0}{1.3} &=& 3.629 \ [m/{sec}^2] \\ A_3 &=& \frac{F – V_E}{T_3} = \frac{4.718 – 2}{0.8} &=& 3.397 \ [m/{sec}^2] \end{eqnarray} $$
と求めることが出来ます。
これら変更した加速期間T1と減速期間T3の加速度(A1とA3)も最大加速度Aよりも小さくなります。
まとめ
今回は、実際に具体的な値を用いて台形速度プロファイルによる軌跡生成を行い、生成した軌跡を量子化することで加速度制限による正確な制御を実現する方法を紹介しました。
今回の記事で紹介した量子化の手法を用いて制御パラメータを変更することで、台形速度プロファイルによるロボットの正確で精密な制御が可能になります。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
