システムを伝達関数で表す：入力ありの質量、ばね、ダンパーによるシステム

ロボット等の自動制御系を取り扱うために、伝達関数を用いる方法があります。

今回は、質量にばねとダンパーが含まれているシステムに対して、伝達関数を求める方法を紹介します。

取り扱うシステム

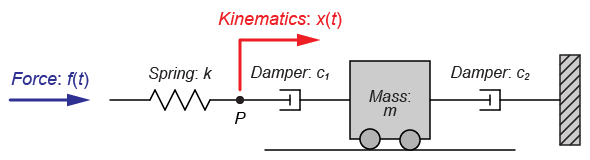
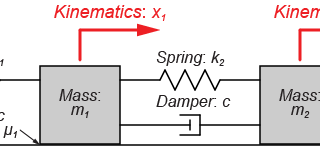
図のように質量$m$とばね$k$、2つのダンパー（$c_1$と$c_2$）からなるシステムを取り扱います。

質量$m$の両端にダンパー（$c_1$、$c_2$）が接続されています。

そして、右側のダンパー$c_2$は、固定された壁に取り付けられています。

さらに、左側のダンパー$c_1$は、ばね$k$に接続されています。

システム内の各パラメータは、

$$m = 10 [kg]$$

$$k = 2 [N/m]$$

$$c_1 = 5 [N \cdot s/m]$$

$$c_2 = 2 [N \cdot s/m]$$

とします。

今回は、このばね$k$の左側から力$f(t)$が加わった時の点$P$の変位$x(t)$について伝達関数$G(s)=\frac{X(s)}{F(s)}$を求めていきます。

運動方程式を求める

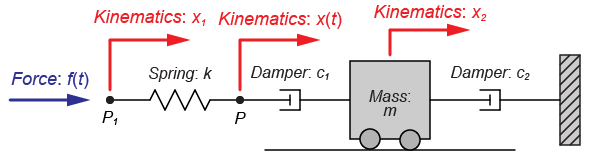
ばねの左側の点（力が加わっている点）$P_1$の変位を$x_1$、質量の変位を$x_2$とします。

この各箇所（$P_1$、$P$、質量$m$）についての運動方程式は、

$$f(t) = 2 (x_1(t) – x(t))$$

$$0 = 2 (x(t) – x_1(t)) + 5 (\dot{x}(t) – \dot{x}_2(t))$$

$$0 = 10 \ddot{x}_2(t) + 5 (\dot{x}_2(t) – \dot{x}(t)) + 2 \dot{x}_2(t)$$

と求めることが出来ます。

この運動方程式についてラプラス変換を行い、時間領域$t$から周波数領域$s$に変換していきます。

ラプラス変換を行う

算出した運動方程式について、ラプラス変換を行います。

$$F(s) = 2 (X_1(s) – X(s))$$

$$0 = 2 (X(s) – X_1(s)) + 5 (s X(s) – s X_2(s))$$

$$0 = 10 s^2 X_2(s) + 5 (s X_2(s) – s X(s)) + 2 s X_2(s)$$

ラプラス変換を行った式について、各変位について整理します。

$$F(s) = 2 X_1(s) – 2 X(s)$$

$$0 = – 2 X_1(s) + (5 s + 2) X(s) – 5 s X_2(s)$$

$$0 = – 5 s X(s) + (10 s^2 + 7 s) X_2(s)$$

この連立方程式を$X(s)$について解くことで、伝達関数$G(s)$を求めていきます。

伝達関数を求める

先程の連立方程式について、1つ目と3つ目の式から変位$X_1(s)$および$X_2(s)$と$X(s)$との関係を求めます。

$$X_1(s) = \frac{F(s)+2 X(s)}{2}$$

$$X_2(s) = \frac{5 s}{10 s^2 + 7 s} X(s)$$

求めた$X_1(s)$と$X_2(s)$の式を2つ目の式に代入し、入力$F(s)$と変位$X(s)$の関係を求めていきます。

$$0 = – (F(s)+2 X(s)) + (5 s + 2) X(s) – 5 s \frac{5 s}{10 s^2 + 7 s} X(s)$$

$$F(s) = \left(-2 + 5 s + 2 – 5 s \frac{5 s}{10 s^2 + 7 s}\right) X(s)$$

$$F(s) = \frac{5 s (10 s^2 + 7 s)- 25 s^2}{10 s^2 + 7 s} X(s)$$

$$F(s) = \frac{50 s^3 + 10 s^2}{10 s^2 + 7 s} X(s)$$

$$F(s) = \frac{50 s^2 + 10 s}{10 s + 7} X(s)$$

これより、求めたい伝達関数$G(s)=\frac{X(s)}{F(s)}$は、

$$G(s)= \frac{X(s)}{F(s)} = \frac{10 s + 7}{50 s^2 + 10 s}$$

となることが分かりました。

まとめ

今回は、質量とばねとダンパーが含まれている機械システムについて、伝達関数を求める方法を紹介しました。