少し複雑な電気回路システムを伝達関数で表す：RLC回路

伝達関数（Transfer Function）を用いたシステムの表現は、ロボットの制御を理解するために重要な手法です。

今回は、抵抗\(R\)、コイル\(L\)、コンデンサ\(C\)が含まれた電気回路を例に、実際にラプラス変換（Laplace Transform）を用いてシステムを伝達関数で表す方法を紹介します。

詳細な解説は、こちらの記事を参考にしてください。

電気回路システムを伝達関数で表す：RLC回路 ロボットを制御するために、伝達関数（Transfer Function）を用いて、ロボットのシステムを数式で表すという方法があり...

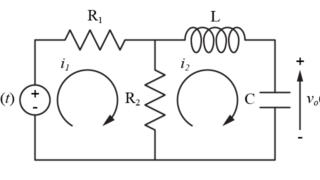
抵抗\(R\)、コイル\(L\)、コンデンサ\(C\)からなる電気回路

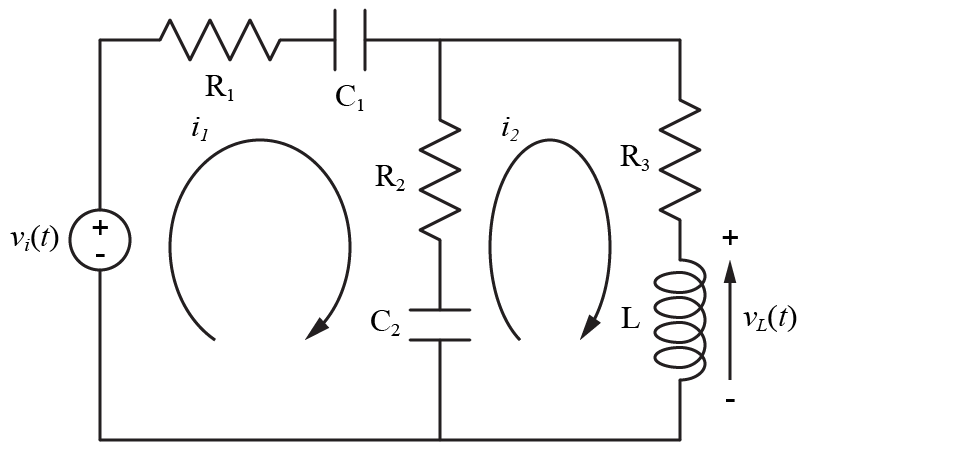
図のような抵抗\(R\)とコイル\(L\)、コンデンサ\(C\)からなる電気回路について、入力\(v_i\)が与えられた時のコイルにかかる電圧\(v_L\)を求めていきます。

回路内の各パラメータは、

$$ R_1 = R_2 = R_3 = 2 [\Omega] $$

$$ L = 2 [H] $$

$$ C_1 = C_2 = 1 [F] $$

として計算します。

このシステムに対し、入力\(v_i\)に対する出力\(v_L\)を求めるために、システムをラプラス変換を用いて時間領域\(t\)から周波数領域\(s\)に変換し、伝達関数を求めていきます。

キルヒホッフの法則を用いて閉回路内での関係式を求める

キルヒホッフの第二法則を用いて、閉回路内での関係式を求めていきます。

今回は、

• 入力\(v_i\)から抵抗\(R_1\)、コンデンサ\(C_1\)を通り、抵抗\(R_2\)、コンデンサ\(C_2\)に行き、入力\(v_i\)に戻る閉回路１と
• 抵抗\(R_3\)、コイル\(L\)（出力\(v_L\)）から、コンデンサ\(C_2\)、抵抗\(R_2\)を通り、抵抗\(R_3\)に戻る閉回路２

を取り扱います。

各閉回路に流れる電流をそれぞれ\(i_1\)、\(i_2\)として、各閉回路についてキルヒホッフの第二法則を用いて関係式を求めていきます。

この二つの閉回路について、それぞれキルヒホッフの第二法則を用いると、

$$ V_i(s) = (R_1 + R_2 + \frac{1}{s C_1} + \frac{1}{s C_2}) I_1(s) – (R_2 + \frac{1}{s C_2}) I_2(s) $$

$$ 0 = (R_2 + R_3 + s L + \frac{1}{s C_2}) I_2(s) – (R_2 + \frac{1}{s C_2}) I_1(s) $$

と表すことが出来ます。

ここで、今回の出力\(v_L(t)\)は、

$$ V_L(s) = s L I_2(s) $$

です。

この出力についての式と、閉回路２についての関係式から、

$$ I_2(s) = \frac{V_L(s)}{s L} $$

$$ I_1(s) = \frac{R_2 + R_3 + s L + \frac{1}{s C_2}}{R_2 + \frac{1}{s C_2}} I_2(s) = \frac{R_2 + R_3 + s L + \frac{1}{s C_2}}{R_2 + \frac{1}{s C_2}} \frac{V_L(s)}{s L} $$

と各電流に対する関係式を求めることが出来ます。

今回のシステムについて、各パラメータは

$$ R_1 = R_2 = R_3 = 2 [\Omega] $$

$$ L = 2 [H] $$

$$ C_1 = C_2 = 1 [F] $$

と定義しています。

このパラメータの値を閉回路１についての関係式と、各電流についての関係式について代入すると、

$$ V_i(s) = (4 + \frac{2}{s}) I_1(s) – (2 + \frac{1}{s}) I_2(s) $$

$$ I_1(s) = \frac{4 + 2 s+ \frac{1}{s}}{2 + \frac{1}{s}} \frac{V_L(s)}{2 s} =  \frac{4 + 2 s+ \frac{1}{s}}{2 s (2 + \frac{1}{s})} V_L(s) $$

$$ I_2(s) = \frac{V_L(s)}{2 s} = \frac{1}{2 s} V_L(s) $$

となります。

これより、各電流についての式を1つ目の閉回路についての関係式に代入すると、

$$ V_i(s) = (4 + \frac{2}{s}) \frac{4 + 2 s+ \frac{1}{s}}{2 s (2 + \frac{1}{s})} V_L(s) – (2 + \frac{1}{s}) \frac{1}{2 s} V_L(s) $$

$$ V_i(s) = \left( (4 + \frac{2}{s}) \frac{4 + 2 s+ \frac{1}{s}}{2 s (2 + \frac{1}{s})} – (2 + \frac{1}{s}) \frac{1}{2 s} \right) V_L(s) $$

$$ V_i(s) = \frac{4 s^2 + 6 s + 1 }{2 s^2} V_L(s) $$

となります。

これより、入力\(V_i(s)\)と出力\(V_L(s)\)の関係\(\frac{V_L(s)}{V_i(s)}\)を示す伝達関数\(G(s)\)は、

$$ G(s) = \frac{V_o(s)}{V_i(s)} = \frac{2 s^2}{4 s^2 + 6 s + 1} $$

と算出することが出来ました。

まとめ

今回は、実際に少し複雑なRLC回路の例を用いて、ロボットの制御に必要な伝達関数の求め方を紹介しました。