ブリッジT回路：周波数特性

ブリッジT回路（Bridged T Network）は、帯域除去フィルタ（Band Rejection Filter）として機能します。

そのため、ブリッジT回路を用いることで、AC（交流）システムの入力信号の特定の周波数を取り除くことが出来ます。

前回は、このブリッジT回路について、入力電圧に対する出力電圧の関係を示す伝達関数を求める方法を紹介しました。

前回の記事はこちら。

ブリッジT回路：伝達関数を求める ブリッジT回路（Bridged T Network）は、AC（交流）システムの入力に対するフィルタとして用いられています。 ...

今回は、求めた伝達関数を用いて周波数特性を求めることで、どの様にブリッジT回路がフィルタとして機能するかを紹介したいと思います。

ブリッジT回路と伝達関数

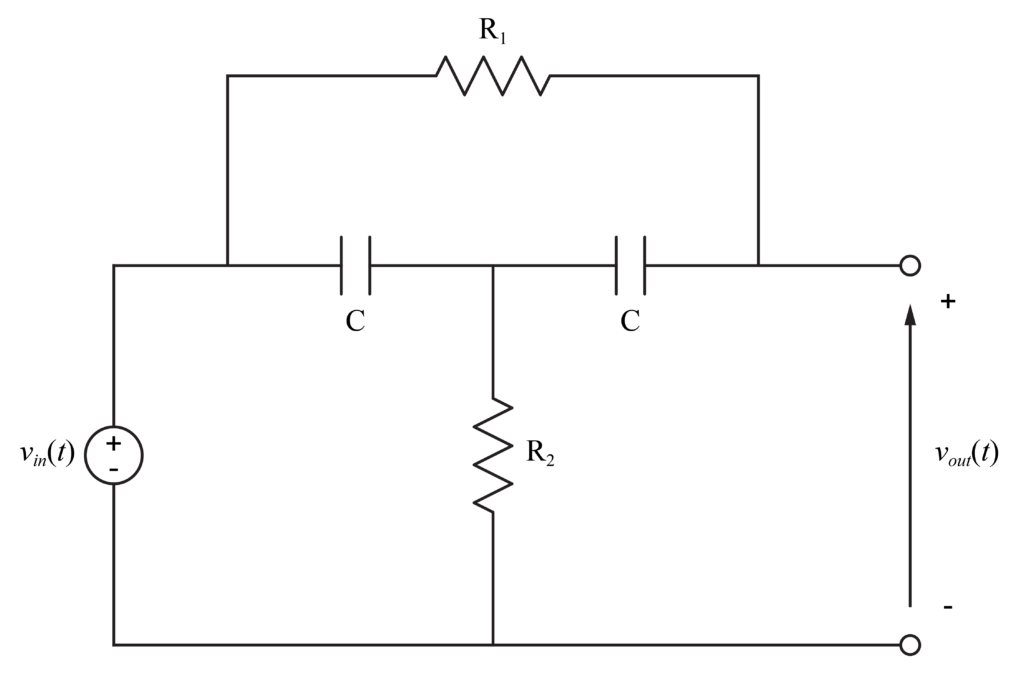
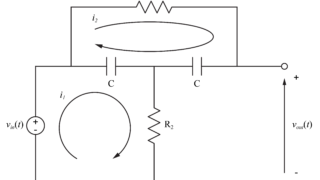
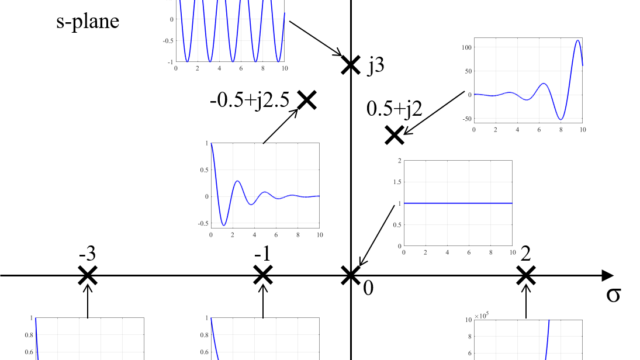
今回取り扱うブリッジT回路は、２つの抵抗\(R_1\)と\(R_2\)と２つのコンデンサ\(C\)で構成されています。

入力された電圧信号\(v_{in}(t)\)が、ブリッジT回路によって特定の周波数帯域が除去されて、出力の電圧信号\(v_{out}(t)\)となります。

このブリッジT回路の伝達関数\(G\)を求めると、

$$ G=\frac{V_{out}(s)}{V_{in}(s)} = \frac{R_1 R_2 C^2s^2 + 2 R_2 Cs+1}{R_1 R_ C^2s^2 + 2 R_2 Cs + R_1 Cs +1} $$

となります。

詳しい求め方は、こちらの記事を参考にしてください。

ブリッジT回路：伝達関数を求める ブリッジT回路（Bridged T Network）は、AC（交流）システムの入力に対するフィルタとして用いられています。 ...

ブリッジT回路の周波数特性

算出した伝達関数\(G\)を用いて、ブリッジT回路の周波数特性を求めていきます。

今回は、回路内の各パラメータ（抵抗とコンデンサ）を、

$$ R_1 = 100 [kHz] $$

$$ R_2 = 1 [kHz] $$

$$ C = 0.01 [\mu F] $$

と定義して、ブリッジT回路の周波数特性をグラフで表したいと思います。

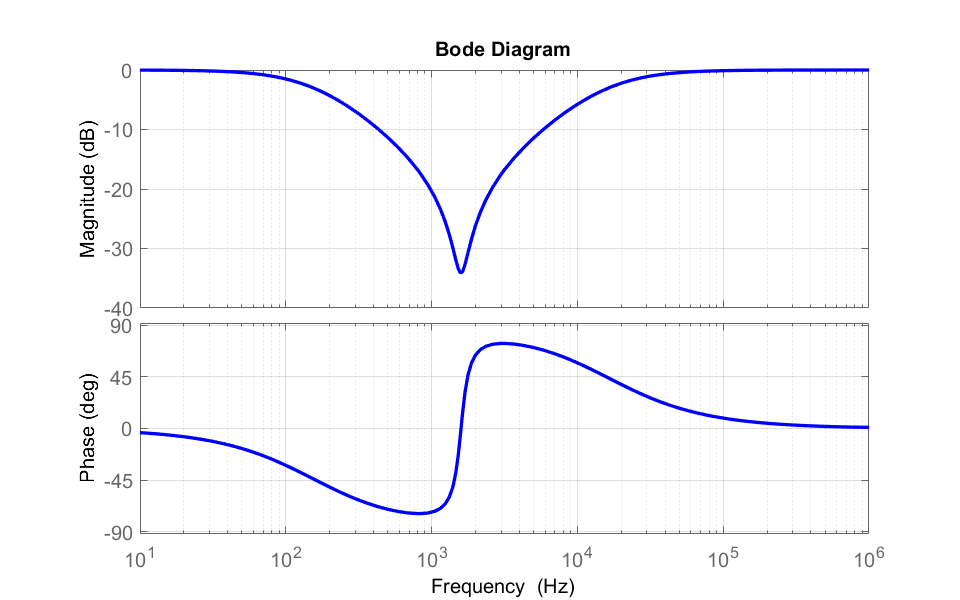
グラフからも分かるように、今回用いたパラメータを用いてブリッジT回路を構成すると、特定の周波数（1.58 [kHz]）で振幅（Magnitude）が小さくなっていることが分かります。

これより、このブリッジT回路をフィルタとして用いることで、特定の周波数帯域の除去が出来ることが分かります。

ブリッジT回路のフィルタ特性

実際に信号\(v_{in}\)をブリッジT回路に入力した時の出力信号\(v_{out}\)の波形を確認してみます。

今回は入力信号\(v_{in}\)として、

$$ v_in(t) = A_1 \sin \left( 2 \pi f_1 t\right) + A_2 \sin \left( 2 \pi f_2 t\right) $$

と２つの周波数が組み合わさった信号を用います。

入力信号内の各パラメータは、

$$ A_1 = 1 [V] $$

$$ A_2 = 0.25 [V] $$

$$ f_1 = 50 [Hz] $$

$$ f_2 = 1500 [Hz] $$

を用います。

よって実際に入力される信号は、

$$ v_in(t) = \sin \left( 100 \pi t\right) + 0.25 \sin \left( 3000 \pi t\right) $$

です。

この入力信号\(v_{in}\)をブリッジT回路に入力した場合の出力信号\(v_{out}\)をグラフで表します。

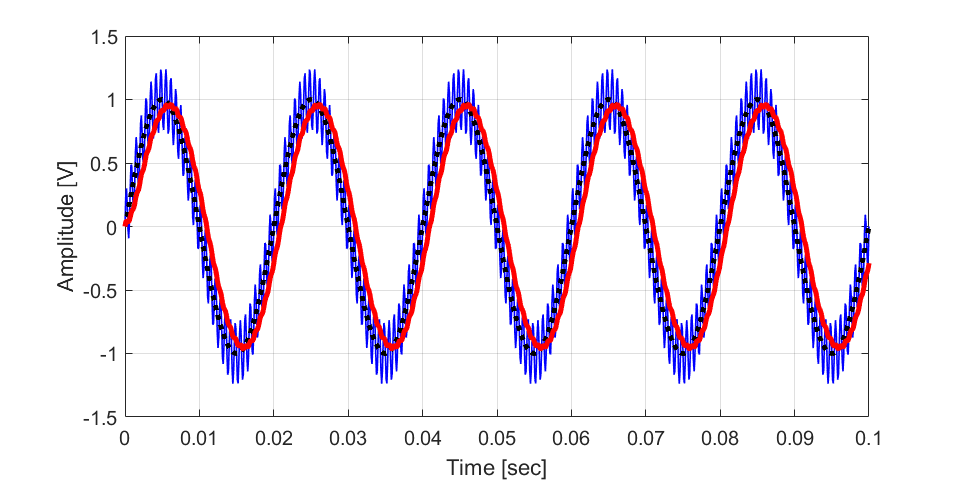
入力信号（青線）は、２つの周波数が混ざり合っていて、高い周波数\(f_2\)によってノイズが乗っているような波形になっています。

この入力波形がブリッジT回路を通したことで周波数\(f_2\)が取り除かれて、出力信号（赤線）は周波数\(f_1\)のみの波形になっていることが分かります。

これは、今回のブリッジT回路が\(1.58 kHz\)周辺の周波数を取り除くフィルタとしての働きを持っており、これにより周波数\(f_2=1.5 kHz\)が取り除かれたためです。

また、出力信号（赤線）は元の入力信号内の周波数\(f_1\)成分（黒線）に対して少し遅れて（右にずれて）います。

これは、ブリッジT回路のフィルタ特性によるもので、先程のボード線図より周波数\(50Hz\)では位相が約17.5度遅れるためです。

まとめ

今回は、ブリッジT回路について帯域除去フィルタとしての特性を、実際に信号を入力した場合の出力信号を見ることで確認しました。