質量‐ばね‐ダンパーシステムのステップ応答（その２）

２次遅れ系システムの伝達関数を求めることで、その伝達関数からシステムのステップ応答の様子を算出することが出来ます。

前回の記事では、質量とばね、ダンパーを含んだモデルを用いて、このモデルの伝達関数を算出し、その固有角周波数と減衰比を算出する方法を紹介しました。

質量‐ばね‐ダンパーシステムのステップ応答 ２次遅れ系システムの伝達関数を求めることで、その伝達関数からシステムのステップ応答の様子を算出することが出来ます。 ...

今回は、質量とばね、ダンパーを含んだモデルの伝達関数から、ステップ応答の様子を算出する方法を紹介します。

質量‐ばね‐ダンパーモデルの伝達関数

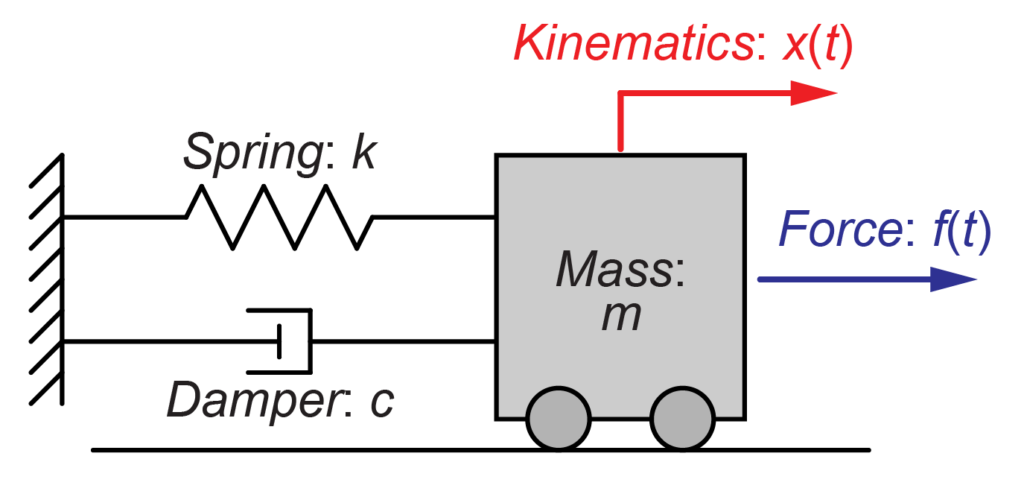
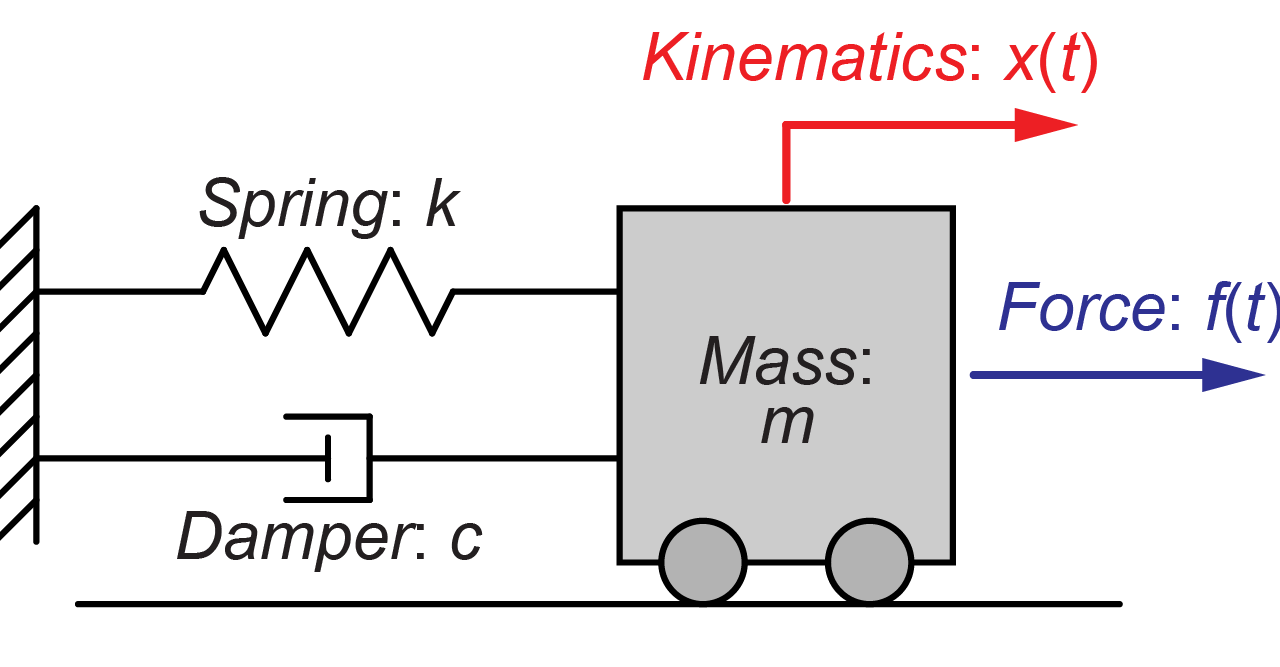
前回に引き続き、上の図のような質量\(m\)がばね\(k\)とダンパー\(c\)を介して壁に接続されているモデルに対し、ステップ入力として力\(f(t)\)を加えた時の質量\(m\)の変位\(x(t)\)を求めていきたいと思います。

今回は、モデル内の各パラメータを

$$ m = 10 [kg] $$

$$ k = 30 [N/m] $$

$$ c = 5 [N/(m/s)] $$

として実際にステップ応答の様子を算出していきます。

この２次遅れ系システムの伝達関数は、

$$ G(s) = \frac{0.1}{s^2 + 0.5 s + 3} $$

となります。

算出の流れについては、こちらの記事を参考にしてください。

質量‐ばね‐ダンパーシステムのステップ応答 ２次遅れ系システムの伝達関数を求めることで、その伝達関数からシステムのステップ応答の様子を算出することが出来ます。 ...

システムのステップ応答

今回取り扱う2次遅れ系システムの伝達関数

$$ G(s) = \frac{0.1}{s^2 + 0.5 s + 3} $$

からステップ入力を与えた際のステップ応答を算出していきます。

各特性の詳しい算出方法は、こちらまたはこちらの記事を参考にしてください。

２次遅れ系システムの伝達関数とステップ応答ロボットなどの動的システムを表した2次遅れ系システムの伝達関数から、システムのステップ入力に対するステップ応答の特性を算出する方法を紹介します。...

２次遅れ系システムの伝達関数とステップ応答（その２） ロボットなどの動的システムを示す伝達関数を用いて、システムの入力に対するシステムの応答の様子を算出することが出来ます。 ...

立ち上がり時間

２次遅れ系システムについて、ステップ応答の立ち上がり時間\(T_r\)は、

$$ T_r = \frac{1.76\zeta^3-0.417\zeta^2+1.039\zeta+1}{\omega_n} $$

で求めることが出来ます。

この式に対して、今回取り扱っているシステムの固有角周波数\(\omega_n\)と減衰比\(\zeta\)の

$$ \omega_n = \sqrt{3} $$

$$ \zeta = 0.144 $$

を代入すると、

$$ T_r = \frac{1.76\cdot {0.144}^3 – 0.417 \cdot {0.144}^2+1.039 \cdot 0.144+1}{\sqrt{3}} $$

$$ = 0.6618 [sec] $$

と立ち上がり時間\(T_r\)を算出することが出来ました。

静定時間

２次遅れ系システムのステップ入力に対する静定時間\(T_s\)は、

$$ T_s = \frac{-\log \left(0.02 \sqrt{1-\zeta^2}\right)}{\zeta {\omega}_n} $$

で求めることが出来ます。

先程と同様に、この式にシステムの固有角周波数\(\omega_n\)と減衰比\(\zeta\)を代入すると、

$$ T_s = \frac{-\log \left(0.02 \sqrt{1-{0.144}^2}\right)}{{0.144} \cdot \sqrt{3}} $$

$$ = 15.73 [sec] $$

と静定時間\(T_s\)を算出することが出来ました。

最大オーバーシュート時間

２次遅れ系システムのステップ入力に対する最大オーバーシュート時間\(T_p\)は、

$$ T_p = \frac{\pi}{\omega_n \sqrt{1 – \zeta^2}} $$

と算出することが出来ます。

よって、この式に固有角周波数\(\omega_n\)と減衰比\(\zeta\)を代入すると、

$$ T_p = \frac{\pi}{\sqrt{3} \sqrt{1 – {0.144}^2}} $$

$$ = 1.833 [sec] $$

と最大オーバーシュート時間\(T_p\)を求めることが出来ました。

最大オーバーシュート量

２次遅れ系システムのステップ応答について、出力の最大オーバーシュート量\(\% OS\)は、

$$ \% OS = 100 e^{-\frac{\zeta \pi}{\sqrt{1 – \zeta^2}}}$$

と算出することが出来ます。

よって、この式に固有角周波数\(\omega_n\)と減衰比\(\zeta\)を代入すると、

$$ \% OS = 100 e^{-\frac{{0.144} \pi}{\sqrt{1 – {0.144}^2}}}$$

$$ = 63.3 [\%] $$

と最大オーバーシュート量\(\% OS\)を求めることが出来ました。

まとめ

今回は、2次遅れ系システムとして質量とばね、ダンパーを含んだモデルを用いて、システムの伝達関数からステップ応答の様子を算出する方法を紹介しました。