ベジエ曲線で離散点を滑らかに補間する

ベジエ曲線を用いることで、離散的な点を滑らかに補間することが出来ます。

このベジエ曲線は、Bスプライン曲線の特殊なケースであるという関係性があります。

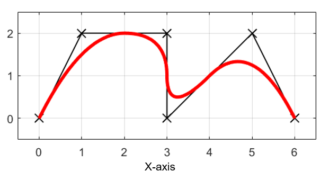
Bスプライン曲線とベジエ曲線の違いは？離散点を補間してみよう！：ロボットの軌跡生成移動ロボットや工作機械などのシステムを目標の場所や状態に移動させるには、目標値を与える必要があります。この目標値...

以前の記事では、Bスプライン曲線を描くためのプログラムを紹介しました。

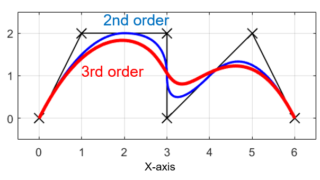
Bスプライン曲線で離散点を補間するプログラムを作成してみた Bスプライン曲線を用いることで、離散点を補間してスムーズな曲線を書くこと出来ます。 https://tajimarobot...

今回の記事では、Bスプライン曲線のプログラムを変換することで、ベジエ曲線を描く方法を紹介します。

Contents

ベジエ曲線とは
ベジエ曲線の作成方法
まとめ

ベジエ曲線とは

ベジエ曲線（ベジェ曲線、Bézier Curve）は、N個の離散的な指令点から得られるN-1次の滑らかな曲線です。

滑らかな曲線を容易に描くことが可能なため、コンピュータグラフィックス分野で広く用いられています。

このベジエ曲線は、Bスプライン曲線のパラメータを制限することで作成が出来るため、ベジエ曲線はBスプライン曲線の特殊な場合という関係性があります。

ベジエ曲線の作成方法

まず、ベジエ曲線とBスプライン曲線のプログラムにおける違いとしては、曲線の次数とノットベクトルの定義にあります。

Bスプライン曲線を描く際には、曲線の次数を自由に決めて、その値を基にノットベクトルのノット数を求めました。

詳しくは、こちらの記事を参考にしてください。

今回の記事で描きたいベジエ曲線の場合は、曲線の次数nを指令点の数pから1引いた値p–1に設定します。

実際には、Bスプライン曲線のプログラムに含まれる曲線の次数nを定義する部分を変更します。

% Control Points (X-Y)
P = [ 
    0.0, 0.0;
    1.0, 2.0;
    3.0, 2.0;
    3.0, 0.0;
    5.0, 2.0;
    6.0, 0.0;
    ];

p = length(P);  % Number of Control Ponits
n = p - 1;          % Degree of Spline (Bezier Curve)
m = p + n + 1;  % Number of Knots in Knot Vector

プログラム内の次数nについて、

$$ n = p – 1 $$

としてプログラムを実行することで、ベジエ曲線を描くことが出来ます。

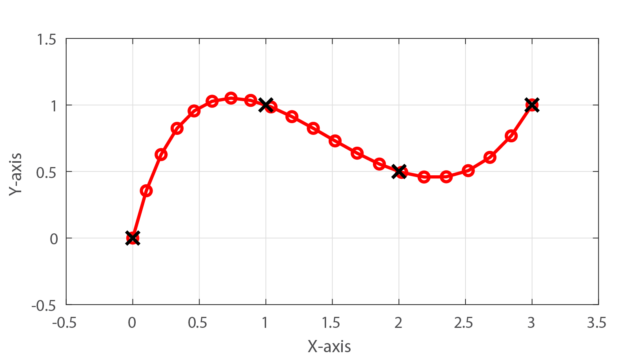
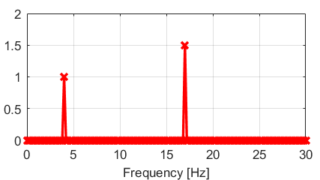
実際にプログラムを変更してベジエ曲線を書いた結果は下のようになります。

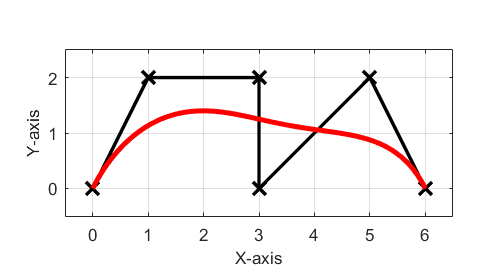
結果から分かるように、与えられた離散点をスムーズな曲線で補間できていることが分かります。

このベジエ曲線を用いることで、ロボットなどに与えられた指令点が離散的でガタガタしていた場合も、滑らかにロボットを動作させることが可能になります。