制御システムの安定性をボード線図を用いて判別する方法を紹介しています。
前回の記事では、開ループ系のボード線図からゲイン余裕(利得余裕)と位相余裕を求める方法を紹介しました。

今回の記事では、求めた安定余裕からシステムの安定性を確認する方法を紹介します。
ボード線図と安定余裕
前回のおさらいです。
ボード線図
開ループ系のボード線図から安定余裕(ゲイン余裕と位相余裕)を求めていきます。
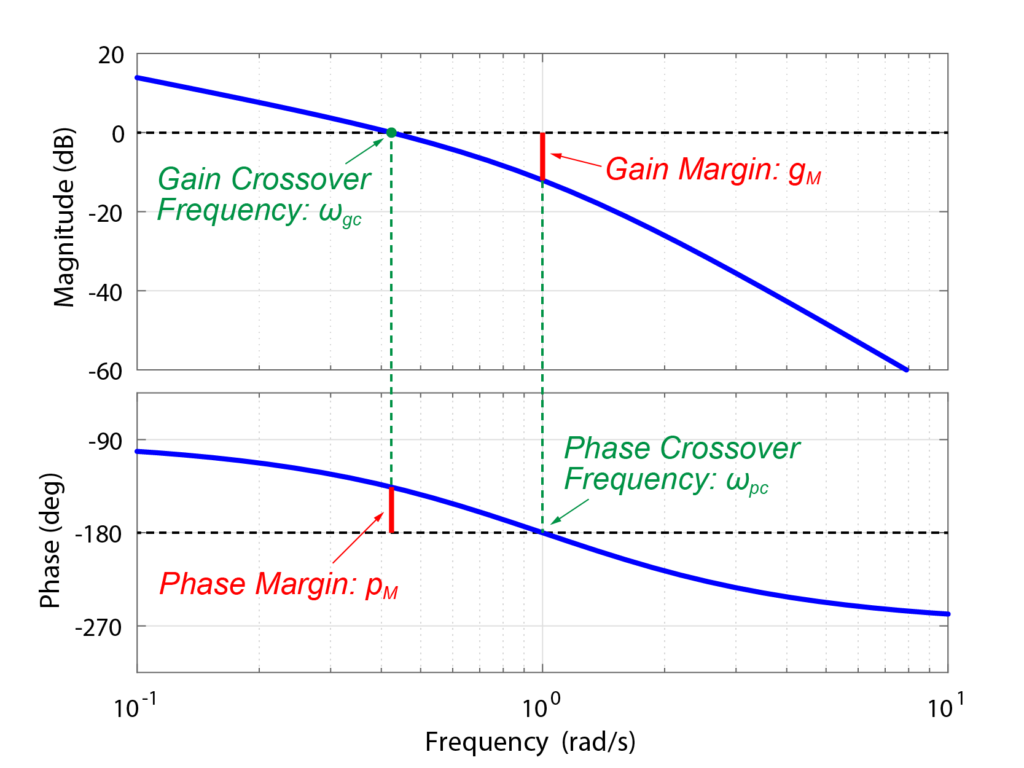
ゲイン余裕
ゲイン余裕は、位相が-180°の時のゲインの値と0dbとの差です。
位相線図で値が-180°となる時の周波数(位相交差周波数)を見つけ、その時のゲイン線図の値を確認します。
そして、その確認した値と0dBとの差を求めることで、ゲイン余裕を算出することが出来ます。
位相余裕
位相余裕は、ゲインが0dbの時の位相の値と-180°との差です。
ゲイン線図で値が0dBとなる時の周波数(ゲイン交差周波数)を見つけ、その時の位相線図の値を確認します。
その値と-180°との差を求めることで、位相余裕を算出することが出来ます。
今回の記事では、これらの算出したゲイン余裕と位相余裕を用いて、システムの安定性を判別する方法を紹介します。
ボード線図による安定性判別
先ほど求めたゲイン余裕と位相余裕を用いてシステムの安定性を判別します。
システムの安定条件
システムが安定である条件としては、
- 位相交差周波数でのゲインの値が負(マイナス)、
- ゲイン交差周波数での位相の値が-180°よりも大きい
場合は、システムは安定であると言えます。
通常、ゲイン余裕は下向きをプラス、位相余裕は上向きをプラスとして算出します。
つまり、ゲイン余裕と位相余裕がともにプラスであれば良いということになります。
安定に設計するための安定余裕
ボード線図から求めたゲイン余裕と位相余裕について、ともにプラスの値であればシステムは安定と言えます。
しかし、あまりにギリギリだとちょっとしたときに不安定になる場合があります。
では、どれくらい余裕があれば安全でしょうか。
一概に言うのは難しいですが、一応として
- サーボ系の場合、ゲイン余裕は12~20dB、位相余裕は40~60°
- プロセス系の場合、ゲイン余裕は3dB以上、位相余裕は20°以上
という目安があります。
実際に安定性をボード線図から求める
では、実際に具体的な値を用いて、ボード線図からシステムの安定性を判別する流れを紹介します。
使用する開ループ伝達関数は、
$$ G(s) = \frac{K}{s \left(s+1\right)^2} $$
です。
この伝達関数に含まれるKをK=0.5にした場合とK=5にした場合のそれぞれについて、システムの安定性確認します。
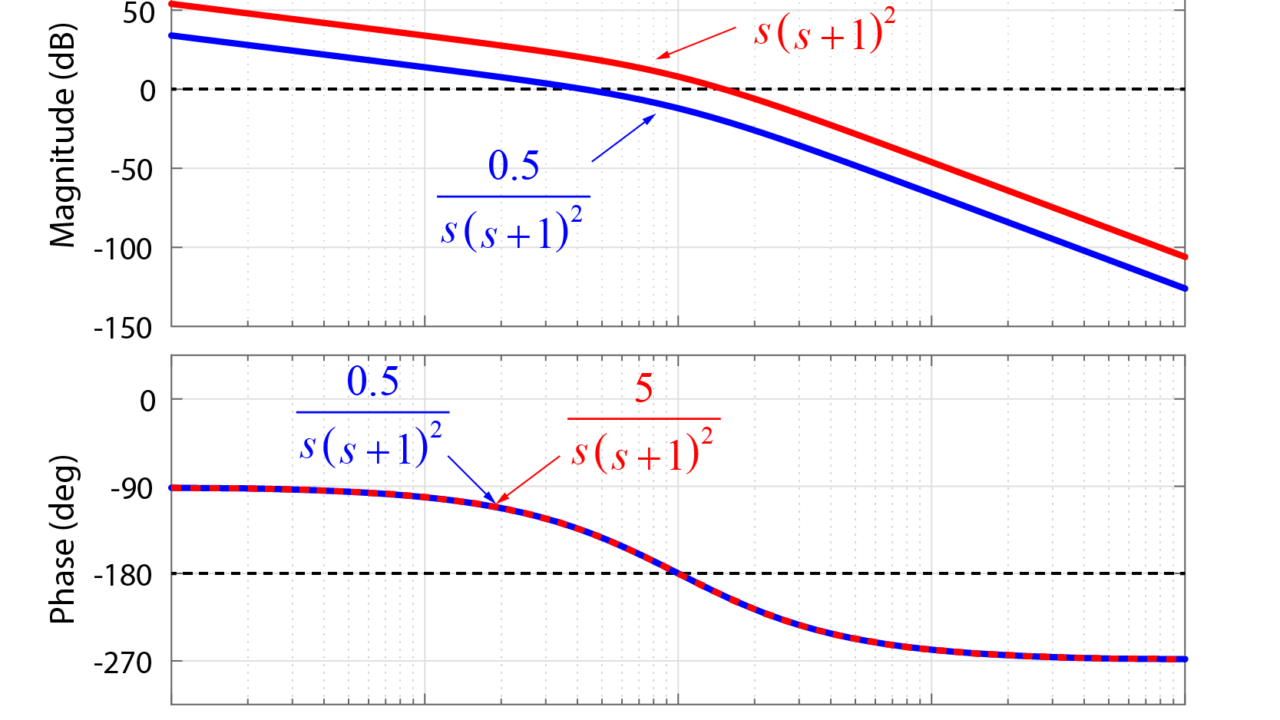
それぞれの開ループ伝達関数について、ボード線図を書いた結果は下の図のようになります。
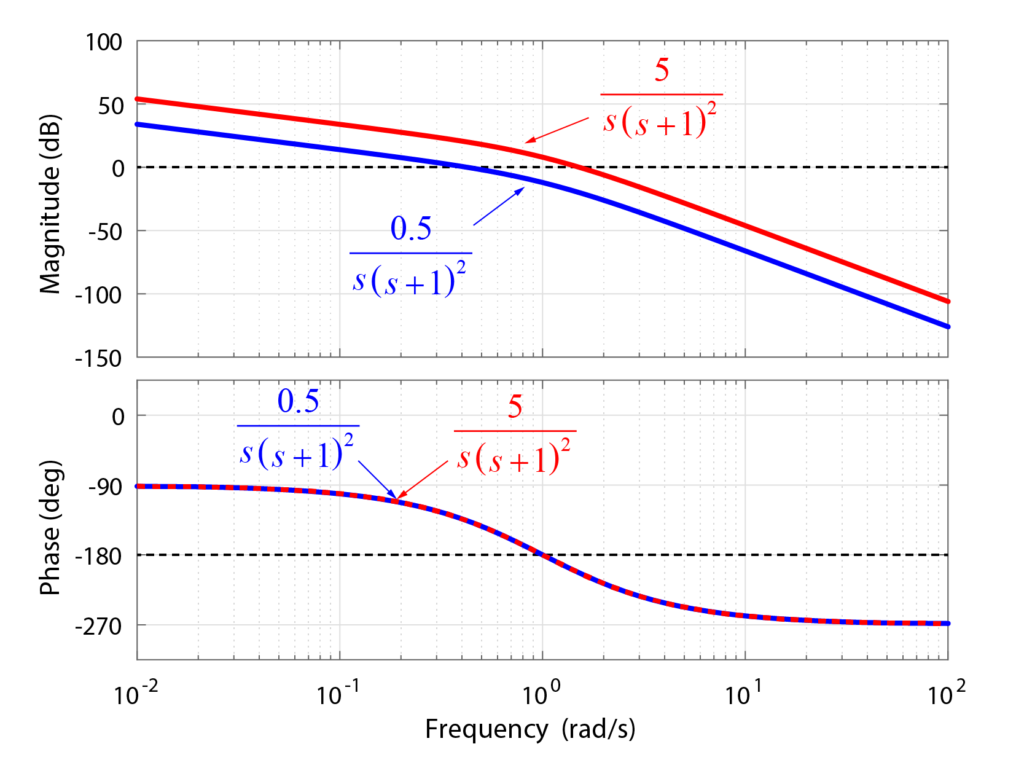
この伝達関数に含まれるKをK=0.5にした場合とK=5にした場合のそれぞれについて、システムの安定性をボード線図から確認していきたいと思います。
K=0.5のとき
与えられた伝達関数について、K=0.5の時の伝達関数は
$$ G(s) = \frac{0.5}{s \left(s+1\right)^2} $$
となります。
この伝達関数G(s)についてのボード線図は下のように表されます。
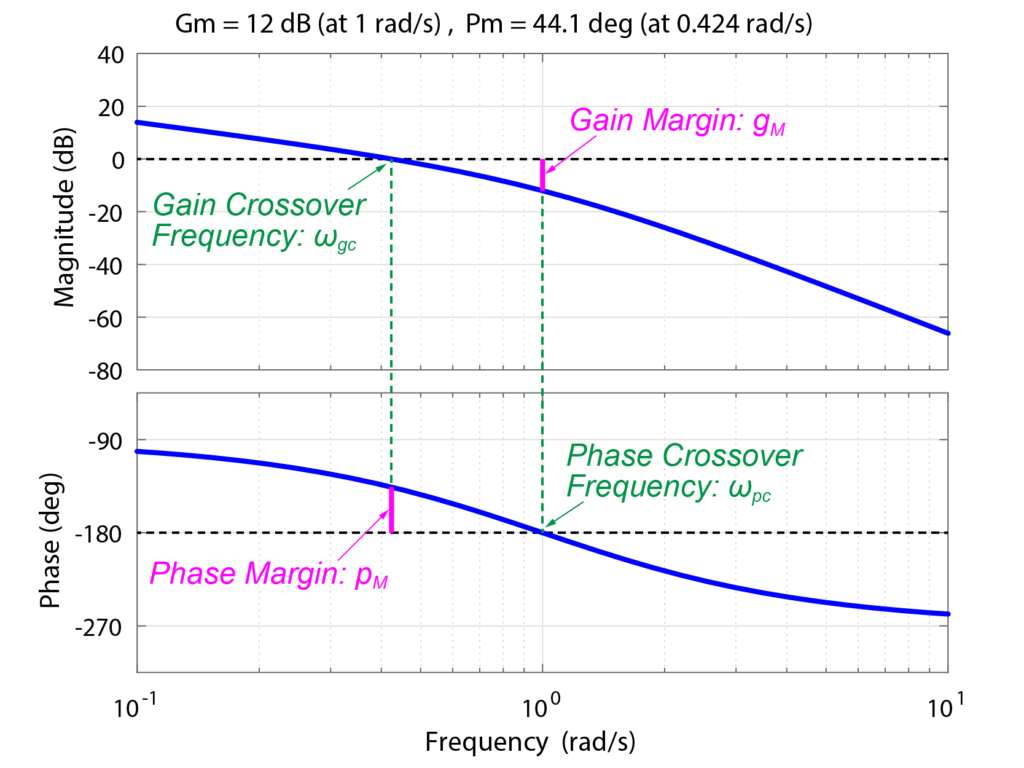
ボード線図から、ゲイン余裕と位相余裕を求めると
$$ \begin{eqnarray} \left\{ \begin{array}{l} g_M = 12 \ [dB] \\ p_M = 44.1 \ [deg] \end{array} \right. \end{eqnarray} $$
となります。
この求めたゲイン余裕と位相余裕は、両方ともプラスの値になっている事が分かります。
よって、このシステムは安定であると言えます。
K=5のとき
伝達関数は
$$ G(s) = \frac{5}{s \left(s+1\right)^2} $$
となります。
この時のボード線図は下の図のように表されます。
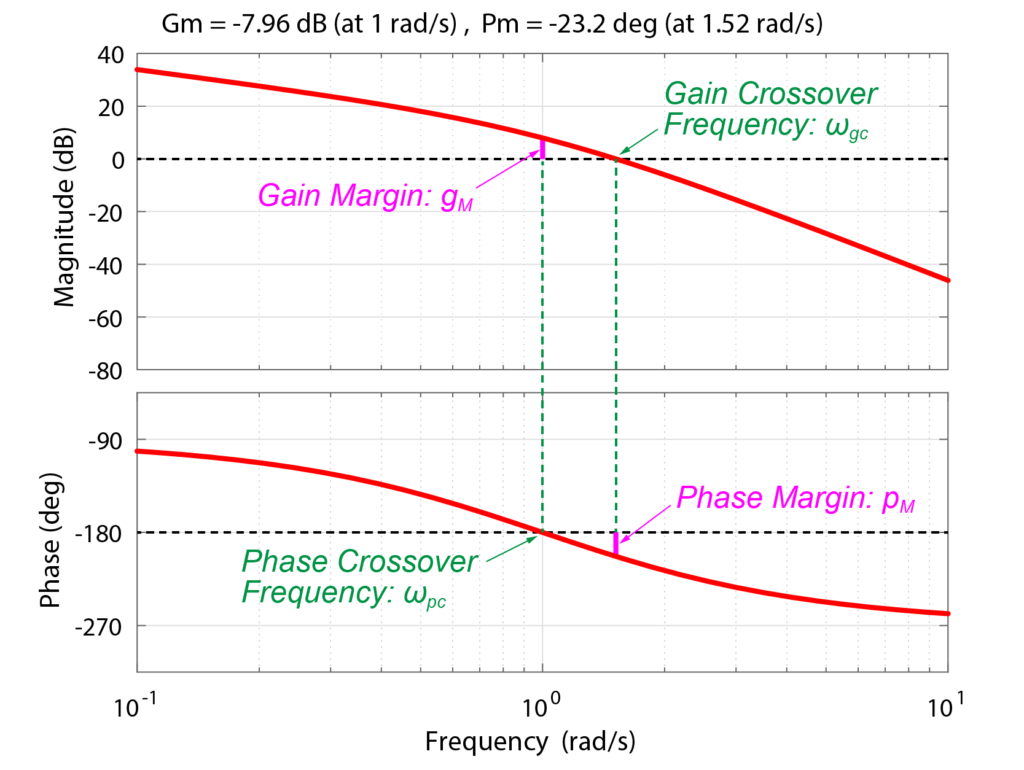
ボード線図から、ゲイン余裕と位相余裕を求めると
$$ \begin{eqnarray} \left\{ \begin{array}{l} g_M = -7.96 \ [dB] \\ p_M = -23.2 \ [deg] \end{array} \right. \end{eqnarray} $$
となります。
この求めたゲイン余裕と位相余裕は、両方ともマイナスの値になっている事が分かります。
よって、このシステムは不安定であると言えます。
まとめ
今回は、開ループ系のボード線図から求めた安定余裕から、システムの安定性を確認する方法を紹介しました。
前回と今回で紹介したボード線図を用いた安定判別法は、システムの特性方程式の取り扱いが難しい場合でも安定性を判別できるという利点があります。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
