台車型倒立振子の安定性と可制御性を確認する

今回のシリーズでは、台車型倒立振子モデルを取り扱い、システムを安定に制御する方法を紹介しています。

前回の記事では、非線形関数で表された台車型倒立振子の状態方程式を線形化する方法を紹介しました。

台車型倒立振子の状態方程式を線形化する今回のシリーズでは、台車型倒立振子モデルを取り扱い、システムを安定に制御する方法を紹介しています。前回までの記事...

今回の記事では、線形化した状態方程式を用いて台車型倒立振子の安定性および可制御性を判別していきたいと思います。

Contents

台車型倒立振子モデルと状態方程式
台車型倒立振子の安定性
制御システムの安定性
まとめ

台車型倒立振子モデルと状態方程式

今回のシリーズ記事では、下の図のような倒立振子（上向きの棒振り子）が台車の上に設置されたモデルを取り扱っています

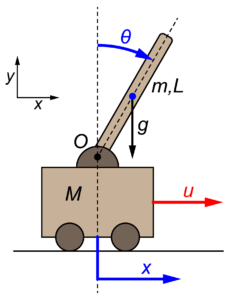
このシステムの状態ベクトルXを

$$ \boldsymbol{ X } = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix} x \\ \dot{x} \\ \theta \\ \dot{\theta} \end{bmatrix} $$

と定義すると、この台車型倒立振子システムの状態方程式は

$$ \begin{eqnarray} \boldsymbol{ \dot{X} } &=& \begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \\ \dot{x}_4 \end{bmatrix} = \begin{bmatrix} f_1(\boldsymbol{X} , u) \\ f_2(\boldsymbol{X} , u) \\ f_3(\boldsymbol{X} , u) \\ f_4(\boldsymbol{X} , u) \end{bmatrix} \\ &=& \begin{bmatrix} x_2 \\ \frac{-\frac{1}{4} m \sin(x_3) \cos(x_3) x_2 x_4 +\frac{1}{6} m L \sin(x_3) {x_4}^2 – \frac{1}{4} m g \sin(x_3) \cos(x_3) + \frac{1}{3} u}{\frac{1}{3} \left( M + m \right) -\frac{1}{4} m \cos^2 (x_3)} \\ x_4 \\ \frac{\frac{1}{4} m L \sin(x_3) \cos(x_3) {x_4}^2 – \frac{1}{2} \left( M + m \right) \sin(x_3) x_2 x_4 – \frac{1}{2} \left( M + m \right) g \sin(x_3) + \frac{1}{2} \cos(x_3) u}{\frac{1}{4} m L \cos^2 (x_3) -\frac{1}{3} \left( M + m \right) L} \end{bmatrix} \end{eqnarray} $$

のように、非線形関数を用いて表すことが出来ます。

この非線形な状態方程式を線形化すると

$$ \dot{\boldsymbol{ X }} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & \frac{- \frac{1}{4} m g}{\frac{1}{3} \left( M + m \right) -\frac{1}{4} m} & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & \frac{- \frac{1}{2} \left( M + m \right) g}{\frac{1}{4} m L -\frac{1}{3} \left( M + m \right) L} & 0 \end{bmatrix} \boldsymbol{ X } + \begin{bmatrix} 0 \\ \frac{\frac{1}{3}}{\frac{1}{3} \left( M + m \right) -\frac{1}{4} m} \\ 0 \\ \frac{\frac{1}{2}}{\frac{1}{4} m L -\frac{1}{3} \left( M + m \right) L} \end{bmatrix} u $$

となり、行列内に含まれる式を整理すると

$$ \dot{\boldsymbol{ X }} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & – \frac{3 m g}{ 4 M + m } & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & \frac{6 \left( M + m \right) g}{ 4 M L + m L} & 0 \end{bmatrix} \boldsymbol{ X } + \begin{bmatrix} 0 \\ \frac{4}{4 M + m} \\ 0 \\ – \frac{6}{4 M L + m L} \end{bmatrix} u $$

のように、状態ベクトルXと入力uを含む線形な状態方程式の形

$$ \dot{\boldsymbol{ X }} = \boldsymbol{ A } \boldsymbol{ X } + \boldsymbol{ B } u $$

で求めることが出来ました。

また、取り扱う台車型倒立振子モデル内のパラメータについて

$$ \begin{eqnarray} \left\{ \begin{array}{l} M = 10 \ [kg] \\ m = 2 \ [kg] \\ L = 1 \ [m] \\ g = 9.8 \ [m/{sec}^2] \end{array} \right. \end{eqnarray} $$

と定義します。

今回の記事では、この線形化した状態方程式を用いて台車型倒立振子モデルの安定性と制御システムの可制御性を確認していきます。

台車型倒立振子の安定性

台車型倒立振子の制御を行う前に、今回取り扱っているモデルの安定性を確認したいと思います。

安定性の確認についての詳細は、こちらの記事を参考にしてください。

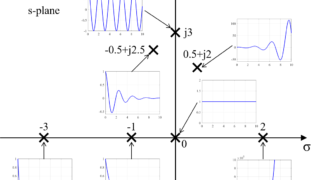
連続的な線形システムの安定性を確認する方法：制御工学入門本シリーズでは、制御工学で学ぶ基本的な知識から実際の応用例までを、なるべく分かりやすく解説しています。 https://t...

線形化した台車型倒立振子モデルの状態方程式

$$ \begin{eqnarray} \dot{\boldsymbol{ X }} &=& \boldsymbol{ A } \boldsymbol{ X } + \boldsymbol{ B } u \\ &=& \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & – \frac{3 m g}{ 4 M + m } & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & \frac{6 \left( M + m \right) g}{ 4 M L + m L} & 0 \end{bmatrix} \boldsymbol{ X } + \begin{bmatrix} 0 \\ \frac{4}{4 M + m} \\ 0 \\ – \frac{6}{4 M L + m L} \end{bmatrix} u \end{eqnarray} $$

について、行列A

$$ \boldsymbol{ A } = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & – \frac{3 m g}{ 4 M + m } & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & \frac{6 \left( M + m \right) g}{ 4 M L + m L} & 0 \end{bmatrix} $$

の固有値λを求めることで、モデルの安定性を確認します。

今回の台車型倒立振子のパラメータを代入した行列A

$$ \boldsymbol{ A } = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & – 1.4 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 16.8 & 0 \end{bmatrix} $$

の固有値λを算出すると

$$ \begin{eqnarray} \left\{ \begin{array}{l} \lambda_1 = 0 \\ \lambda_2 = 0 \\ \lambda_3 = 4.0988 \\ \lambda_4 = -4.0988 \end{array} \right. \end{eqnarray} $$

となります。

ここで、実数部が正（プラス）の固有値λ₃が含まれています。

そのため、今回の台車型倒立振子モデルは不安定であると言えます。

制御システムの安定性

先の計算により、本記事で取り扱っている台車型倒立振子モデル単体では不安定であることが分かりました。

そのため、入力uを用いてシステム全体を安定に制御する必要があります。

そこで、台車型倒立振子システムの可制御性を確認していきます。

可制御性の確認方法についての詳細は、こちらの記事を参考にしてください。

線形システムの可制御性を判定する方法：制御工学入門　本シリーズでは、制御工学で学ぶ基本的な知識から実際の応用例までを、なるべく分かりやすく解説しています。 https://t...

線形化した状態方程式に含まれる行列AとベクトルB

$$ \begin{eqnarray} \left\{ \begin{array}{l} \boldsymbol{ A } = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & – \frac{3 m g}{ 4 M + m } & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & \frac{6 \left( M + m \right) g}{ 4 M L + m L} & 0 \end{bmatrix} \\ \boldsymbol{ B } = \begin{bmatrix} 0 \\ \frac{4}{4 M + m} \\ 0 \\ – \frac{6}{4 M L + m L} \end{bmatrix} \end{array} \right. \end{eqnarray} $$

を用いて行列Co

$$ \boldsymbol{ Co } = \begin{bmatrix} \boldsymbol{ B } & \boldsymbol{ A } \boldsymbol{ B } & \boldsymbol{ A }^2 \boldsymbol{ B } & \cdots & \boldsymbol{ A }^{n-1} \boldsymbol{ B } \end{bmatrix} $$

の階数

$$ \mathrm{ rank } \left( \boldsymbol{ Co } \right) $$

を求めて、システムの可制御性を確認します。

今回の台車型倒立振子システムのパラメータを代入した行列AとベクトルB

$$ \begin{eqnarray} \left\{ \begin{array}{l} \boldsymbol{ A } = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & – 1.4 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 16.8 & 0 \end{bmatrix} \\ \boldsymbol{ B } = \begin{bmatrix} 0 \\ 0.0952 \\ 0 \\ -0.1429 \end{bmatrix} \end{array} \right. \end{eqnarray} $$

より、行列Coは

$$ \boldsymbol{ Co } = \begin{bmatrix} 0 & 0.0952 & 0 & 0.2000 \\ 0.0952 & 0 & 0.2000 & 0 \\ 0 & -0.1426 & 0 & -2.4000 \\ -0.1429 & 0 & -2.4000 & 0 \end{bmatrix} $$

となるため、階数は

$$ \mathrm{ rank } \left( \boldsymbol{ Co } \right) = 4 $$

となり、状態変数の要素数（n=4）と一致します。

よって、今回の台車型倒立振子システムは可制御性があることが分かりました。