本シリーズでは、制御工学で学ぶ基本的な知識から実際の応用例までを、なるべく分かりやすく解説しています。
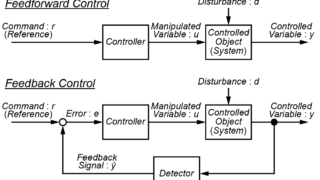
前回までの記事では、世の中にある動的システムと制御方法、そしてフィードバック制御の重要性について紹介しました。
今回からの記事では、固有値と固有ベクトルを用いて常微分方程式で表された線形システムを解析する方法を説明していきたいと思います。
線形システムと常微分方程式
線形システムの状態方程式は
$$ \dot{\boldsymbol{ x }} = \boldsymbol{ A } \boldsymbol{ x } $$
という常微分方程式を用いて表されます。
ここで、xはn次元の状態変数ベクトルで、Aはn×nの行列で状態変数ベクトルxがどのように変化するかを表しています。
状態ベクトルの微分方程式を解く
この様な微分方程式の一般解は
$$ \begin{eqnarray} \begin{array}{l} \dot{x} = a x \\ \Rightarrow x(t) = e^{a t} x(0) \end{array} \end{eqnarray} $$
と求めることが出来ます。
よって、与えられた線形システムの常微分方程式解くと、
$$ x(t) = e^{\boldsymbol{ A } t} x(0) $$
という一般解になります。
しかし、注目してほしいのは自然数eのべき数に行列Aが含まれています。
そのため、行列Aに対する処理が必要になります。
テイラー展開を適用
ここで、行列Aはn×nの正方行列なので、テイラー展開を用いて
$$ e^{\boldsymbol{ A } t} = \boldsymbol{ I } + \boldsymbol{ A } t + \frac{\boldsymbol{ A }^2 t^2}{2!} + \frac{\boldsymbol{ A }^3 t^3}{3!} + \cdots $$
と表すことが出来ます。
よって、線形システムの解は
$$ \begin{eqnarray} x(t) &=& e^{\boldsymbol{ A } t} x(0) \\ &=& \left[ \boldsymbol{ I } + \boldsymbol{ A } t + \frac{\boldsymbol{ A }^2 t^2}{2!} + \frac{\boldsymbol{ A }^3 t^3}{3!} + \cdots \right] x(0) \end{eqnarray} $$
となりました。
テイラー展開を用いて自然数eのAt乗を含む一般解を表す方法は分かりました。
では、実際にどうやって計算すれば良いでしょう。
テイラー展開後の式には行列Aのn乗が含まれています。
この計算は難しく、複雑で、計算に時間がかかります。
そこで、行列Aの固有値（Eigenvalue）と固有ベクトル（Eigenvector）を用いる手法が重要になります。
まとめ
今回は、常微分方程式で表された線形システムの状態方程式の一般解について紹介しました。
状態ベクトルxの一般解を求めるためには、行列Aのn乗という複雑で難しく時間のかかる計算が必要になります。
次回は、線形システムの解を簡単に求めるために、行列Aの固有値（Eigenvalue）と固有ベクトル（Eigenvector）を用いた方法を紹介します。
ELEGOO Arduinoスターターキット
UNO R3スマートロボットカー
Raspberry Pi 3 Model b+
