離散的な線形システムの安定性を確認する方法：制御工学入門

本シリーズでは、制御工学で学ぶ基本的な知識から実際の応用例までを、なるべく分かりやすく解説しています。

制御工学入門制御工学（Control Engineering）についての情報を紹介します。動的システムと制御方法世の中にあふれる動的...

前回の記事では、常微分方程式で表された連続時間での線形システムの安定性を確認する方法を紹介しました。

連続的な線形システムの安定性を確認する方法：制御工学入門本シリーズでは、制御工学で学ぶ基本的な知識から実際の応用例までを、なるべく分かりやすく解説しています。 https://t...

しかし、この世の中には連続的なシステムのみではなく、たくさんの離散的なシステムが存在します。

今回の記事では、この離散時間での線形システムの安定性を確認する方法を紹介していきたいと思います。

Contents

離散時間システムの状態方程式
離散時間システムの安定性
おまけ
まとめ

離散時間システムの状態方程式

前回の記事で取り扱った常微分方程式

$$ \dot{\boldsymbol{ x }} = \boldsymbol{ A } \boldsymbol{ x } $$

は連続時間の線形システムの状態方程式を表しています。

しかし、世の中のシステムには離散的な時間で表された離散的システムが多く存在します。

これら離散時間システムの状態方程式は

$$ \boldsymbol{ x }(k+1) = \boldsymbol{ \tilde{A} } \boldsymbol{ x }(k) $$

と表すことが出来ます。

ここで、x_kはサンプルk番目の状態xを表していて

$$ \boldsymbol{ x }(k) = \boldsymbol{ x }(k \Delta t) $$

のようにサンプル時間Δtを用いて表されます。

そして、離散時間システムの状態方程式に含まれる$\boldsymbol{ \tilde{A} }$は連続時間システムの状態方程式に含まれる行列Aを用いて

$$ \boldsymbol{ \tilde{A} } = e^{\boldsymbol{ A } \Delta t} $$

という式で求められます。

今回は、この離散的な時間で表された線形システムについて安定性を確認していきます。

離散時間システムの安定性

離散的な線形システムの安定性を確認する方法を紹介していきます。

まず、システムに与えられるサンプリング時間k=0での初期値をx₀と設定します。

このとき、サンプリング時間k=1での状態x₁は、離散的な線形システムの状態方程式を用いて

$$ \boldsymbol{ x_1 } = \boldsymbol{ \tilde{A} } \boldsymbol{ x_0 } $$

と求めることが出来ます。

そして、サンプリング時間k=2での状態x₂は、状態x₁と状態方程式を用いて

$$ \begin{eqnarray} \boldsymbol{ x_2 } &=& \boldsymbol{ \tilde{A} } \boldsymbol{ x_1 } \\ &=& \boldsymbol{ \tilde{A} } \boldsymbol{ \tilde{A} } \boldsymbol{ x_0 } \\ &=& {\boldsymbol{ \tilde{A} }}^2 \boldsymbol{ x_0 } \end{eqnarray} $$

となります。

同様に、サンプリング時間k=3での状態x₃は

$$ \begin{eqnarray} \boldsymbol{ x_3 } &=& \boldsymbol{ \tilde{A} } \boldsymbol{ x_2 } \\ &=& \boldsymbol{ \tilde{A} } {\boldsymbol{ \tilde{A} }}^2 \boldsymbol{ x_0 } \\ &=& {\boldsymbol{ \tilde{A} }}^3 \boldsymbol{ x_0 } \end{eqnarray} $$

と算出できます。

よって、サンプリング時間k=nでの状態x_nは

$$ \boldsymbol{ x_n } = {\boldsymbol{ \tilde{A} }}^n \boldsymbol{ x_0 } $$

と表すことが出来ます。

このx_nについて式からも分かるように、初期状態x₀が与えられた場合に$\boldsymbol{ \tilde{A} }$を用いることで、未来の値を求めることが出来ます。

ここで、$\boldsymbol{ \tilde{A} }$の固有値λとすると

$$ \begin{eqnarray} \begin{array}{ll} \boldsymbol{ x_1 } = \boldsymbol{ \tilde{A} } \boldsymbol{ x_0 } & \lambda \\ \boldsymbol{ x_2 } = {\boldsymbol{ \tilde{A} }}^2 \boldsymbol{ x_0 } & {\lambda}^2 \\ \boldsymbol{ x_3 } = {\boldsymbol{ \tilde{A} }}^3 \boldsymbol{ x_0 } & {\lambda}^3 \\ \boldsymbol{ x_n } = {\boldsymbol{ \tilde{A} }}^n \boldsymbol{ x_0 } & {\lambda}^n \\ \end{array} \end{eqnarray} $$

という関係性が導かれます。

（詳しくは記事下部のおまけを参照してください。）

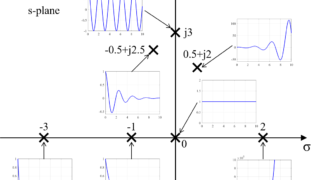
ここで、固有値λは常に上の図のように実部σと虚部ωで表されます。

この固有値λの大きさをR、角度をθとすると固有値λは

$$ \lambda = R e^{i \theta} $$

のように書き換えることが出来ます。

そして、状態x_nに対するλⁿは

$$ {\lambda}^n = R^n e^{i n \theta} $$

と表すことが出来ます。

この式で、e^inθは回転（角度）のみを表しており、大きさには影響はありません。

よって、Rが1より大きいければλⁿは無限大に発散し、Rが1より小さければ0に収束することが分かります。

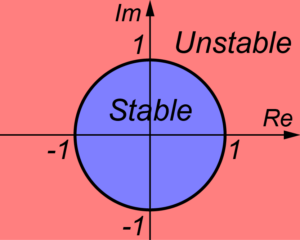
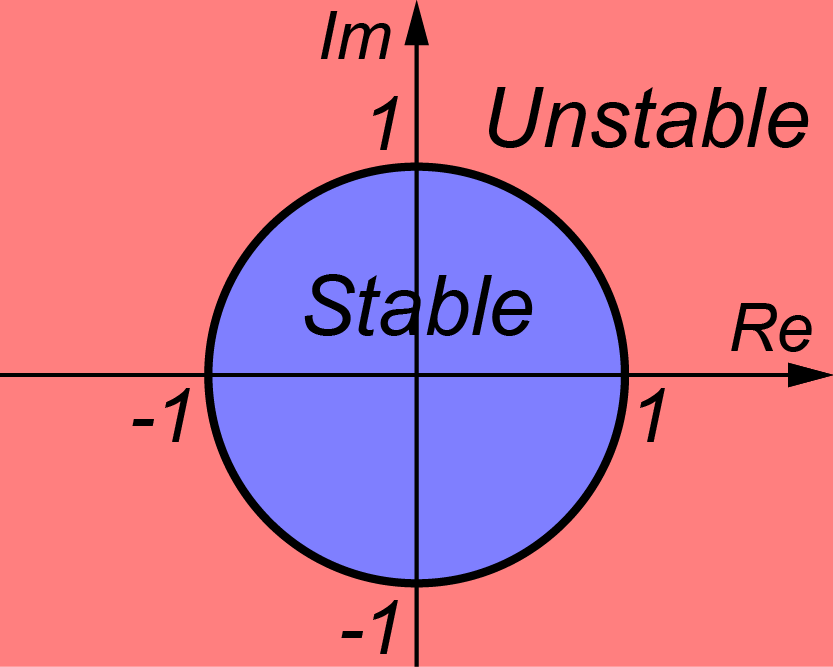
ここで、長さが１の単位円を書きます。

この円の中に固有値λが存在するとシステムは安定となります。

言い換えると、固有値λが円の外に存在した場合、システムは不安定になります。

おまけ

以前のシリーズ記事でも紹介した通り、連続時間システムの場合

$$ \begin{eqnarray} \begin{array}{l} \boldsymbol{ A } \boldsymbol{ T } = \boldsymbol{ T } \boldsymbol{ D } \\ \Rightarrow \boldsymbol{ A } = \boldsymbol{ T } \boldsymbol{ D } {\boldsymbol{ T }}^{-1} \end{array} \end{eqnarray} $$

という関係性が成り立ちます。

離散時間システムでも同様で

$$ \begin{eqnarray} \begin{array}{l} \boldsymbol{ \tilde{A} } \boldsymbol{ \tilde{T} } = \boldsymbol{ \tilde{T} } \boldsymbol{ \tilde{D} } \\ \Rightarrow \boldsymbol{ \tilde{A} } = \boldsymbol{ \tilde{T} } \boldsymbol{ \tilde{D} } {\boldsymbol{ \tilde{T} }}^{-1} \end{array} \end{eqnarray} $$

という関係性が成り立ちます。