加速度(Acceleration)の単位時間当たりの変化率を表すものとして、躍度(Jerk、加加速度)があります。
今回は、この躍度を用いてロボットの軌跡生成(Trajectory Generation)をする方法を紹介します。
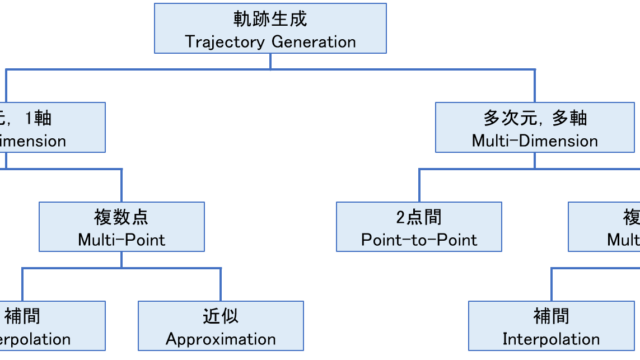
躍度とは
躍度(Jerk)とは
- 加速度の単位時間当たりの変化率
です。
通常、躍度はjと表されます。
加速度aに対して時間tについての時間微分をすることで
$$ j = \frac{da}{dt} $$
と躍度j求めることが出来ます。
また、速度vや変位xについても、
$$ j = \frac{d^2 v}{dt^2} = \frac{d^3 x}{dt^3} $$
と2階微分、3階微分をすることでも求めることができます。
軌跡生成に躍度を使うメリット
加速度を制御(制限)した軌跡生成の手法として、台形速度プロファイル(Trapezoidal Velocity Profile)があります。
台形速度を用いた軌跡生成については、こちらの記事を参考にしてください。
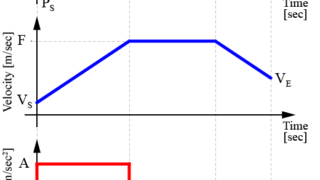
この台形速度プロファイルでは、速度は連続的に変化します。
一方、加速度はパルス状になっており、加減速の開始時や終了時に急激な変化が生じます。
この急激な変化がロボットの制御に影響を及ぼすことがあります。
そこで、よりスムーズにロボットを制御するために、躍度を用いた連続的な加速度波形を用いての軌跡生成が必要となります。
躍度制限加速度プロファイル
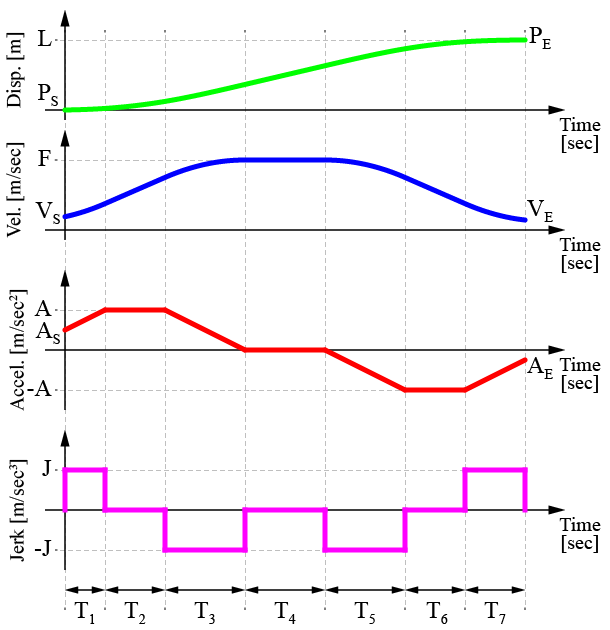
上の図のような、躍度を制限して行う軌跡生成の手法を躍度制限加速度プロファイル(Jerk Limited Acceleration Profile、JLAP)と言います。
加減速時の躍度を考慮することで、加速度波形の傾きを制御することが出来ます。
これよりパルス状であった加速度の急激な変化を台形の連続的な変化に変更することが出来ました。
このような加速度波形を台形加速度プロファイル(Trapezoidal Acceleration Profile)と言います。
その結果、速度プロファイルもよりスムーズに変化をさせることが可能となります。
まとめ
今回は、躍度制限を利用した台形加速度の軌跡生成方法を紹介しました。
躍度を制御することで、台形の加速度、S字の速度プロファイルの作成が可能になります。
次回は、この躍度制限台形加速度プロファイルを実際に作成するために必要な、各期間の時間を算出する方法を紹介したいと思います。
























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
