システムがどのように振動するかを求める方法にモード解析(Modal Analysis)があります。
2質量システムを例にモード解析の使い方を説明していきます。
モード解析とは
モード解析とは、力学モデルと基にして、システムの振動についてその周波数や振幅を解析するための方法です。
システムの運動方程式を用いて固有値解析を行うことで、振動の周波数(周期)や各周波数での振幅を算出することが出来ます。
2質量システムの運動方程式
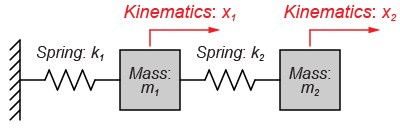
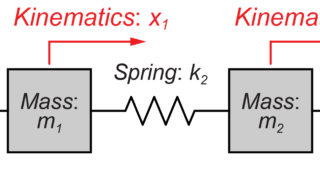
図のように2つの質量(\(m_1\)と\(m_2\))が、それぞればね(\(k_1\)と\(k_2\))によって壁と互いに接続されているモデルを扱います。
各パラメータについて、
$$ m_1 = m_2 = m $$
$$ k_1 = 3 k $$
$$ k_2 = 2 k $$
とすると、この2質量モデルの運動方程式は、
$$ \begin{eqnarray} \left\{ \begin{array}{l} m \ddot{x}_1(t) + 5 k x_1(t) – 2 k x_2(t) = 0 \\ m \ddot{x}_2(t) – 2 k x_1(t) + 2 k x_2(t) = 0 \end{array} \right. \end{eqnarray} $$
となります。
固有値解析を用いて振動の周波数を求める
2質量モデルの運動方程式を行列式の形にすると、
$$ m \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} \ddot{x}_1(t) \\ \ddot{x}_2(t) \end{bmatrix} + k \begin{bmatrix} 5 & -2 \\ -2 & 2 \end{bmatrix} \begin{bmatrix} x_1(t) \\ x_2(t) \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$
と置き換えることが出来ます。
ここで、
$$ M = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} $$
$$ K = \begin{bmatrix} 5 & -2 \\ -2 & 2 \end{bmatrix} $$
とすると、
$$ \det \left(K – M \omega^2 \right) = 0 $$
を解くことで振動の周波数\(\omega\)を求めることが出来ます。
$$ \det \left(K – M \omega^2 \right) = 0 $$
$$ \Rightarrow \det \left(\begin{bmatrix} 5 & -2 \\ -2 & 2 \end{bmatrix} – \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \omega^2 \right) = 0 $$
$$ \Rightarrow \det \left(\begin{bmatrix} 5 & -2 \\ -2 & 2 \end{bmatrix} – \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \omega^2 \right) = 0 $$
$$ \Rightarrow \det \left(\begin{bmatrix} 5 – \omega^2 & -2 \\ -2 & 2 – \omega^2 \end{bmatrix} \right) = 0 $$
$$ \Rightarrow \left(5 – \omega^2\right) \left(2 – \omega^2\right) – 4 = 0 $$
$$ \Rightarrow \omega^4 – 7 \omega^2 + 6 = 0 $$
よって、振動の周波数は、
$$ {\omega_1}^2 = 1 $$
$$ {\omega_2}^2 = 6 $$
となります。
モード解析で振動の振幅を求める
システムの運動方程式から、
$$ \left(5 – \omega^2\right) x_1 – 2 x_2 = 0 $$
と1つ目の式を用いて振幅を算出していきます。
ここで、\(x_1\)の振幅を
$$ x_1 = 1 $$
とすると、\(x_2\)の振幅は
$$ x_2 = \frac{5 – \omega^2}{2} $$
となります。
この関係式を用いて、先に求めた各周波数について、\(x_1=1\)とした際の\(x_2\)の振幅を求めていきます。
周波数\({\omega_1}^2 = 1\)について、この値を先の関係式に代入すると、
$$ x_2 = \frac{5 – 1}{2} = 2 $$
となります。
同様に、周波数\({\omega_2}^2 = 6\)について、
$$ x_2 = \frac{5 – 6}{2} = -\frac{1}{2} $$
となります。
よって、各周波数(\(\omega_1\)と\(\omega_2\))に対する振幅(\(X_1\)と\(X_2\))は、
$$ X_1 = \begin{bmatrix} 1 \\ 2 \end{bmatrix} $$
$$ X_2 = \begin{bmatrix} 1 \\ – \frac{1}{2} \end{bmatrix} $$
と表すことが出来ました。
まとめ
今回は、モード解析(Modal Analysis)を用いて、2質量システムがどのように振動するかを求める方法を紹介しました。
次回は、求めた周波数と振幅を用いて、実際のシステム内の質量の運動(\(x_1(t)\)と\(x_2(t)\))を求めていきたいと思います。
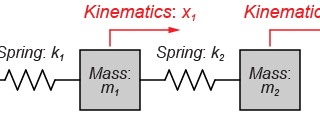

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+

2質点の運動についてこのサイトで勉強させて頂いています。ありがとうございます。
勉強不足で申し訳ないのですが教えて頂きたい事があります。
運動方程式から行列式を解く際に、「各質点の位置xは互いに同じ振動数で位相差が無い」という仮定を置いてると思うのですが、なぜこの仮定で良いのでしょうか。
2質点だと振動数も位相も異なるように思えるのですが。。
お手数ですがご教授頂けると幸いです。
コメントありがとうございます。
ご質問の中に記載いただいた「各質点の位置は互いに同じ振動数で位相差が無い」という仮定は少しニュアンスが異なるかと思います。
本記事で取り扱っているシステムは2質点のシステムのため、システムの運動は2つのモード(振動数と位相)の組み合わせによる運動となります。
ただ各質点は同じ動きをするという訳ではなく、2つのモードの異なる組み合わせによる運動をします。
各質点の運動を構成する2つの振動数と位相の成分は同じですが、それぞれのモードの割合(振幅など)が異なるため、結果的に2質点は異なる運動をします。
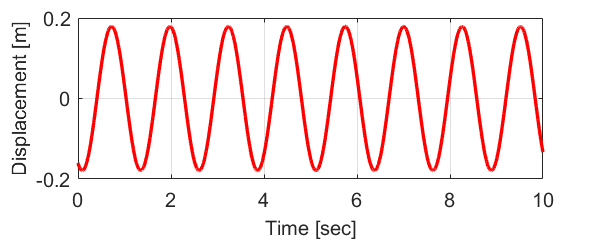
こちらの記事に求めた振動数と位相による2質点の運動の様子を表したグラフがあるので、ご確認いただければと思います。
https://tajimarobotics.com/mode-analysis-3/
参考になれば幸いです。