台形速度プロファイルの軌跡を量子化してロボットを精密制御する

ロボットの軌跡を生成する際に、加速度を制限した台形速度プロファイルを用いることで、ロボットを滑らかに制御することが出来ます。

ロボットの軌跡生成：加速度制限を用いて台形速度プロファイルを作成する ロボットの軌跡を生成する際に重要な項目として、 モータの出力できる限界を使って 短い時間で移動する という...

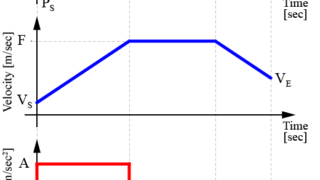
実際に、生成した軌跡を用いてロボットを正確に制御するためには、制御の周期やサンプリング時間に合わせた量子化（Quantization）が必要となります。

以前の記事では、一定速度でロボットを制御するシンプルなシステムについて、軌跡の量子化を行う方法を紹介しました。

軌跡生成の量子化をしてロボットを正確に制御する 加速度制限や躍度制限による軌跡を生成することで、滑らかにロボットを制御できます。 以前の記事でも、これらの軌跡生成...

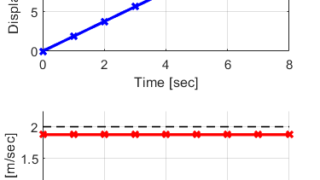
今回の記事では、加速度制限による台形速度プロファイルによる軌跡生成について、量子化を行う方法を紹介します。

台形速度プロファイルと一般式

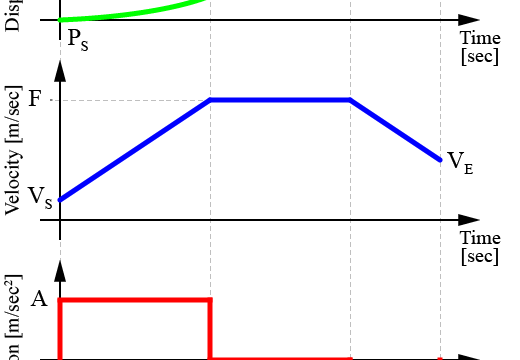
加速度制限による台形速度プロファイルでの軌跡生成をした様子は、下の図のようになります。

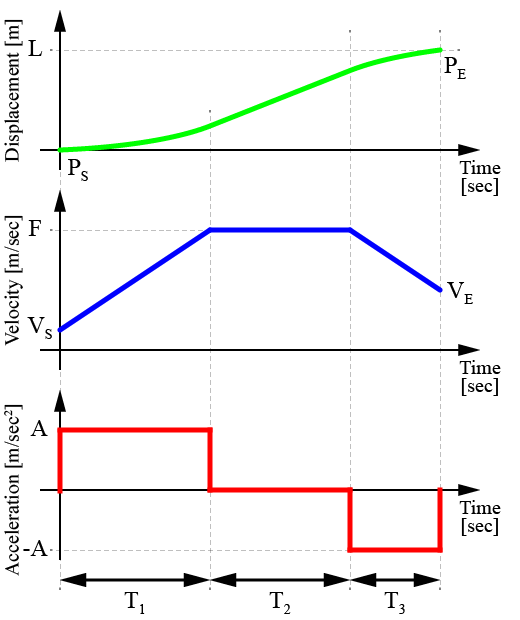
軌跡生成の際に台形速度プロファイルを用いることで、

• 最大加速度と最大速度の制御と、
• 滑らかで最短時間での制御

を可能にします。

台形速度プロファイルの一般式

台形速度プロファイルを作成するためには、軌跡に含まれるパラメータとして各期間の時間（加速期間T₁、巡航期間T₂、減速期間T₃）を求める必要があります。

加速期間T₁と減速期間T₃は、ロボットの最大速度Fと最大加速度A、そして初速V_Sと終速V_Eから

$$ \begin{eqnarray} T_1 &=& \frac{F – V_S}{A} \\ T_3 &=& \frac{F – V_E}{A} \end{eqnarray} $$

と求められます。

ここで、V_SとV_Eはロボットの初速と終速です。

もし、停止状態のロボットを制御し、制御終了時にも停止させたい場合は、この初速V_Sと終速V_Eは0になります。

算出した期間（T₁とT₃）をもとに、各期間での移動距離（L₁とL₃）を求めると、

$$ \begin{eqnarray} L_1 &=& \frac{\left( F + V_S \right) T_1}{2} \\ L_3 &=& \frac{\left( F + V_E \right) T_3}{2} \end{eqnarray} $$

となります。

これより、巡航期間T₂は移動させたい距離Lと巡航（最大）速度F、そして残りの期間での距離（L₁とL₃）より

$$ T_2 = \frac{L – L_1 – L_3}{F} $$

と算出することが出来ます。

これら算出した各期間より、台形速度プロファイルを作成します。

巡航期間が無い場合

ロボットの最大速度Fや最大加速度Aに対して移動距離Lが短い場合、巡航期間T₂がなくなる場合があります。

この場合、生成される軌跡は加速期間T₁と減速期間T₃のみになり、軌跡の速度も最大速度Fより低くなります。

前の項で紹介した巡航期間T₂を求める式

$$ T_2 = \frac{L – L_1 – L_3}{F} $$

より算出した値が0よりも小さい場合、

$$ T_2 < 0 \Rightarrow T_2 = 0 $$

のように巡航期間T₂を0に設定します。

この巡航期間T₂が無い場合の速度のピークF_Pは

$$ F_P = \sqrt{\frac{2 A L + {V_S}^2 + {V_E}^2}{2}} $$

と算出できるため、加速期間と減速期間は

$$ \begin{eqnarray} T_1 &=& \frac{F_P – V_S}{A} \\ T_3 &=& \frac{F_P – V_E}{A} \end{eqnarray} $$

と求めることが出来ます。

加速度制限プロファイルの量子化

これまでに紹介した式を用いて算出したパラメータ（加速期間T₁、巡航期間T₂、減速期間T₃）より、台形速度軌跡の量子化を行います。

つまり、各期間（T₁、T₂、T₃）をサンプリング時間T_sの整数倍にします。

そして、速度Vおよび加速度Aの値を各期間にあわせて調整することで、精密な制御を実現します。

制御期間を量子化する

まずはじめに生成した軌跡の移動時間（T₁、T₂、T₃）をサンプリング時間T_sに合わせて変更します。

天井関数を用いて、各期間の制御時間（移動時間）をサンプリング時間T_sの何倍にすればよいかを求めます。

$$ \begin{eqnarray} \left\{ \begin{array}{l} N_1 &=& \lceil \frac{T_1}{T_s} \rceil \\ N_2 &=& \lceil \frac{T_2}{T_s} \rceil \\ N_3 &=& \lceil \frac{T_3}{T_s} \rceil \end{array} \right. \end{eqnarray} $$

そして求めたN_iとサンプリング時間T_sより、各期間での制御時間T_iは

$$ \begin{eqnarray} \left\{ \begin{array}{l} T_1 &=& N_1 T_s \\ T_2 &=& N_2 T_s \\ T_3 &=& N_3 T_s \end{array} \right. \end{eqnarray} $$

と求めることが出来ます。

天井関数を使った制御時間の変換についての詳細は、こちらの記事を参考にしてください。

軌跡生成の量子化をしてロボットを正確に制御する 加速度制限や躍度制限による軌跡を生成することで、滑らかにロボットを制御できます。 以前の記事でも、これらの軌跡生成...

パラメータを変更する

変更した各期間の制御時間に合わせて、巡航期間T₂での速度Fと加速期間T₁と減速期間T₃での加速度Aを変更します。

まず、サンプリング時間T_sに合わせて変更後の各期間（T₁、T₂、T₃）と移動距離L、そしてロボットの初速V_Sと終速V_Eより

$$ F = \frac{2 L – V_S T_1 – V_E T_3}{T_1 + 2 T_2 + T_3} $$

のように量子化後の移動速度Fを求めます。

この求めた移動速度Fを用いて、加速期間T₁と減速期間T₃での加速度は

$$ \begin{eqnarray} A_1 &=& \frac{F – V_S}{T_1} \\ A_3 &=& \frac{F – V_E}{T_3} \end{eqnarray} $$

と求めることが出来ます。

まとめ

今回の記事では、加速度制限を用いた台形速度プロファイルについて、生成した軌跡の量子化を行う方法を紹介しました。

今回紹介した量子化の方法を用いてパラメータを変更することで、台形速度プロファイルによるロボットの正確で精密な制御が可能になります。

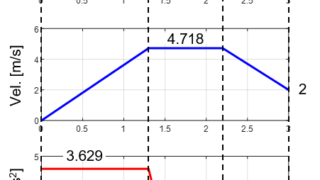
次回の記事では、実際に具体的な値を用いて台形速度制御の量子化を行う流れを紹介したいと思います。

加速度を制限して生成した軌跡を量子化して機械を正確に制御する 加速度制限による台形速度制御を行うことで、ロボットや機械を滑らかに動作させることが出来ます。 https://tajima...