フィードバックシステムと伝達関数の極と根軌跡

高い次数の伝達関数を含む複雑なフィードバックシステムの特性を根軌跡によって可視化することが出来ます。

根軌跡で制御システムを設計する 根軌跡を用いることで、取り扱いが難しい高い次数の伝達関数を含む複雑なフィードバックシステムの特性を可視化することができます。 ...

今回は、具体的なフィードバックシステムの伝達関数を用いて、システムのパラメータが変化した際の極の動きを求めていきます。

フィードバックシステムと極

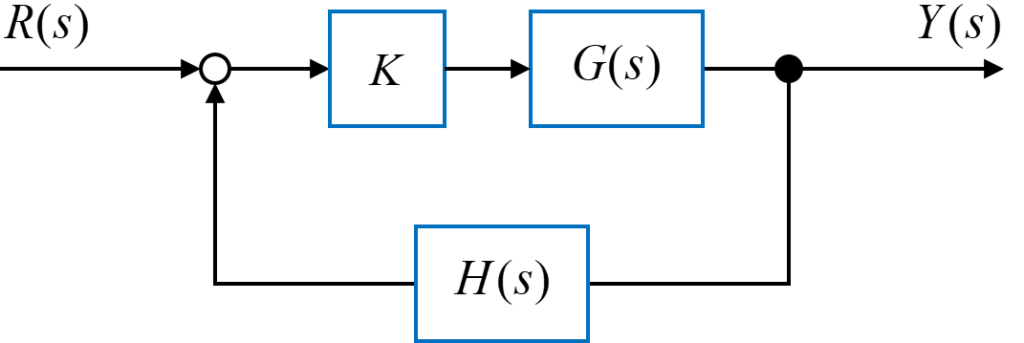
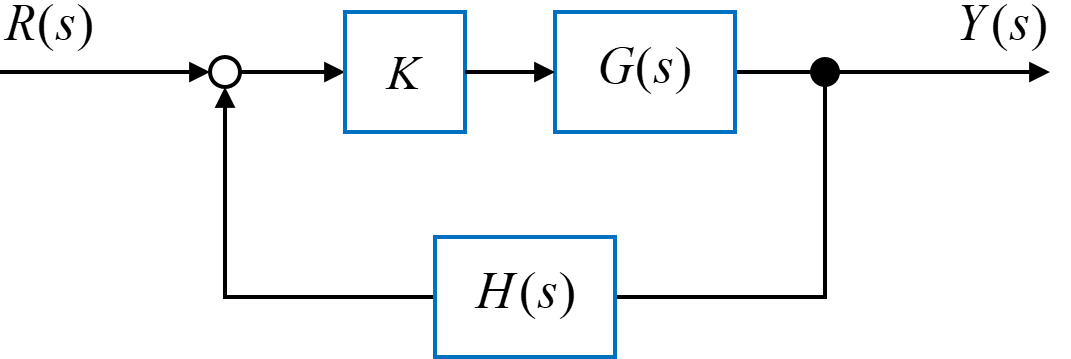
図のようなフィードバックシステム全体の伝達関数\(T(s)\)は

$$ T(s) = \frac{K G(s)}{1 + K G(s) H(s)} $$

と求めることが出来ます。

ここで、フィードフォワード伝達関数\(G(s)\)を

$$ G(s) = \frac{1}{s (s+4)} $$

として、フィードバック伝達関数\(H(s)\)を

$$ H(s) = 1 $$

とすると、このフィードバックシステム全体の伝達関数\(T(s)\)は

$$ T(s) = \frac{K \frac{1}{s (s+4)}}{1 + K \frac{1}{s (s+4)}} $$

$$ = \frac{K}{s^2 + 4s + K} $$

と求めることが出来ます。

このシステム全体の伝達関数\(T(s)\)の極は、伝達関数の分母が\(0\)になる際の\(s\)の値になるので、

$$ s^2 + 4s + K = 0 $$

で求められる解\(s\)が今回のフィードバックシステム全体の極になります。

この式をシステムの特性方程式\(D(s)\)

$$ D(s) = s^2 + 4s + K $$

と言います。

パラメータの変化と極

先ほど求めた特性方程式\(D(s)\)について、様々な値のパラメータ\(K\)で解くことでシステムのパラメータ\(K\)が変化した際の極の変化を求めていきます。

システムのパラメータ\(K\)を0から10まで変化させた際のシステム全体の伝達関数の極は下記のように算出することが出来ます。

$$ \begin{eqnarray} \begin{array}{c|c|c} K & pole 1 & pole 2 \\ \hline 0 & 0 & -4 \\ 1 & -0.2679 & -3.7321 \\ 2 & -0.5858 & -3.4142 \\ 3 & -1 & -3 \\ 4 & -2 & -2 \\ 5 & -2+j1 & -2-j1 \\ 6 & -2+j1.4142 & -2-j1.4142 \\ 7 & -2+j1.7321 & -2-j1.7321 \\ 8 & -2+j2 & -2-j2 \\ 9 & -2+j2.2361 & -2-j2.2361 \\ 10 & -2+j2.4495 & -2-j2.4495 \\ \end{array} \end{eqnarray} $$

この表を用いて、各ゲインにおける2つの極の位置を複素平面上に表すと下図のように表されます。

図より、2つの極はパラメータ\(K\)の上昇とともに互いに近づき、\(K=4\)の時に2つの極が同じ位置になり、\(K>4\)となると上下に分かれて\(\pm \infty \)（無限大）に向かいます。

この図のように、システムのパラメータ（ゲイン）を変えた際の閉回路の極の位置の移動の軌跡を表したものを根軌跡と言います。

根軌跡の特徴

フィードバック系の伝達関数\(T(s)\)が

$$ T(s) = \frac{K G(s)}{1 + K G(s) H(s)} $$

で表されるとき、このシステム全体の極は伝達関数\(T(s)\)の分母より

$$ 1 + K G(s) H(s) = 0 $$

と求めることが出来ます。

この式より、パラメータ\(K\)、フィードフォワード伝達関数\(G(s)\)、フィードバック伝達関数\(H(s)\)について

$$ K G(s) H(s) = -1 $$

という関係式を導くことが出来ます。

ここで、

$$ K G(s) H(s) $$

を開回路伝達関数と言います。

この開回路伝達関数について、先ほど求めた関係式より

$$ K G(s) H(s) = 1 \angle \left(2k+1\right) 180^{ \circ } $$

$$ k = 0, \pm 1, \pm 2, \pm 3, \cdots $$

と表すことが出来ます。

これより、開回路伝達関数の大きさは

$$ \left| K G(s) H(s) \right| = 1 $$

となり、角度は

$$ \angle K G(s) H(s) = \left(2k+1\right) 180^{ \circ } $$

と求められます。

また、パラメータ（ゲイン）\(K\)をフィードフォワード伝達関数\(G(s)\)とフィードバック伝達関数\(H(s)\)を用いて表すと

$$ K = \frac{1}{|G(s)| |H(s)|} $$

となります。

パラメータと極と根軌跡

今回用いているフィードバックシステムの開回路伝達関数は

$$ K G(s) H(s) = \frac{K}{s (s+4)} $$

です。

この伝達関数に先ほど求めた表のパラメータ\(K\)の値と対応する極の値を代入すると

$$ K = 3 ,  pole = -1 \Rightarrow $$

$$ K G(s) H(s) = \frac{3}{-1 (-1+4)}= \frac{3}{-3}=-1 $$

や

$$ K = 8 ,  pole = -2 – j2 \Rightarrow $$

$$ K G(s) H(s) = \frac{8}{\left(-2 – j2\right) (-2 – j2+4)}= \frac{8}{\left(-2 – j2\right) (2 – j2)}= \frac{8}{-8}=-1 $$

と\(-1\)になる事が確認できます。

まとめ

今回は、実際に具体的なフィードバックシステムの伝達関数を用いて、制御システムのパラメータが変化した際の伝達関数の極の動きを求めました。

そして、このパラメータが変化した際の極の移動の経路を表したものを根軌跡ということも紹介しました。

次回は、実際に根軌跡を描く方法を紹介していきたいと思います。

根軌跡を構成する伝達関数の極の位置 前回の記事では、制御システムのパラメータが変化した際の伝達関数の極の動きを求めて根軌跡を求めました。 https://ta...