システムの定常偏差：入力信号と制御系の出力信号との偏差

ロボットや機械などを制御する際に、システムの制御系が安定であることはとても重要です。

そのような安定な制御系について、目標値を入力した際のシステムの出力値が時間経過しても目標値まで到達せず、ある一定の偏差（誤差）が生じることがあります。

このような偏差を定常偏差（Steady-state Error）と言います。

今回は、代表的な入力信号が安定なシステムに与えられた際の定常偏差を算出する方法を紹介します。

Contents

定常偏差とは
定常偏差を求める一般式
各入力に対する定常偏差の求め方
まとめ

定常偏差とは

定常偏差とは、安定な制御システムについて入力された目標値と出力される制御値との定常状態での偏差の事を言います。

定常偏差が生じるシステムでは、時間が無限大∞に経過してもシステムの出力値が入力された目標値に到達しません。

そのため、このような定常偏差が生じるシステムかどうかを事前に確認することはとても重要になってきます。

定常偏差を求める一般式

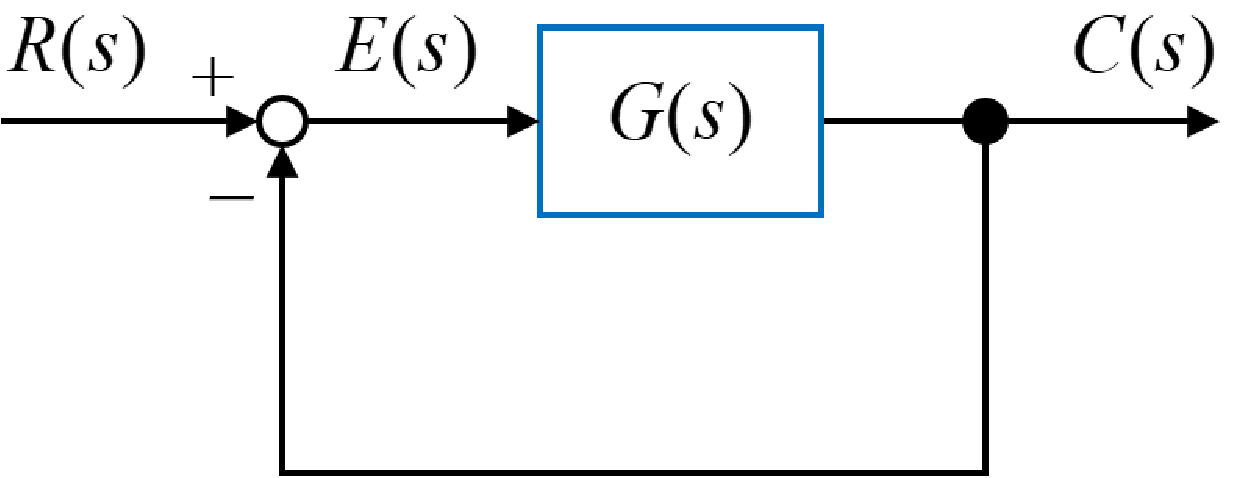
一般的なフィードバック制御を用いて、定常偏差の一般式を求めていきます。

システム内の伝達関数に入力される信号は、目標値R(s)（入力）と制御値C(s)（出力）の差で求められます。

よって、この偏差E(s)は

$$ E(s) = R(s) – C(s) $$

で表されます。

また、制御値C(s)は偏差E(s)と伝達関数G(s)より、

$$ C(s) = G(s) E(s) $$

となります。

よって、フィードバックシステムの偏差E(s)は、

$$ \begin{eqnarray} E(s) = R(s) – G(s) E(s) \\ E(s) + G(s) E(s)= R(s) \\ E(s) \left(1+G(s)\right)= R(s) \\ \Rightarrow E(s) = \frac{R(s)}{1+G(s)} \end{eqnarray} $$

で表すことが出来ます。

この偏差E(s)について最終値の定理を用いると、

$$ \begin{eqnarray} e(\infty) &=& \displaystyle \lim_{ t \to \infty } e(t) = \displaystyle \lim_{ s \to 0 } s E(s) \\ &=& \displaystyle \lim_{ s \to 0 } \frac{s R(s)}{1+G(s)} \end{eqnarray} $$

と時刻$t$が$\infty$になった場合の偏差を求めることが出来ます。

この時刻t=∞での偏差e(∞)が定常偏差になります。

各入力に対する定常偏差の求め方

代表的な入力信号の種類として

ステップ入力
ランプ入力（定速度入力）
パラボラ入力（定加速度入力）

の３種類を用いて、各入力が与えられた際のフィードバックシステムの定常偏差の求め方を紹介します。

ステップ入力の場合

ステップ入力r(t)=u(t)をラプラス変換すると、

$$ R(s) = \frac{1}{s} $$

となります。

この式を先程の定常偏差e(∞)を表す式に代入すると、

$$ \begin{eqnarray} e_{step}(\infty) &=& \displaystyle \lim_{ s \to 0 } \frac{s \frac{1}{s}}{1+G(s)} \\ \Rightarrow e_{step}(\infty) &=& \displaystyle \lim_{ s \to 0 } \frac{1}{1+G(s)} \end{eqnarray} $$

と表されます。

この式を用いることで、制御値としてステップ入力u(t)が与えられた際のフィードバックシステムの定常偏差e_step(∞)を求めることが出来ます。

ランプ入力（定速度入力）の場合

ステップ入力u(t)の場合と同様に、ランプ入力tu(t)が与えられた場合の定常偏差を表す式を求めていきます。

ランプ入力r(t)=tu(t)をラプラス変換すると、

$$ R(s) = \frac{1}{s^2} $$

となります。

よって、この関係式を定常偏差e(∞)の式に代入して、

$$ \begin{eqnarray} e_{ramp}(\infty) &=& \displaystyle \lim_{ s \to 0 } \frac{s \frac{1}{s^2}}{1+G(s)} = \displaystyle \lim_{ s \to 0 } \frac{1}{s+sG(s)} \\ \Rightarrow e_{ramp}(\infty) &=& \displaystyle \lim_{ s \to 0 } \frac{1}{sG(s)} \end{eqnarray} $$

と、制御値としてランプ入力tu(t)が与えられた際のフィードバックシステムの定常偏差e_ramp(∞)を求めることが出来ます。

パラボラ入力（定加速度入力）の場合

先程と同様に、パラボラ入力r(t)=t²u(t)をラプラス変換すると、

$$ R(s) = \frac{1}{s^3} $$

と表されます。

このラプラス変換後の式を定常偏差e(∞)の式に代入することで

$$ \begin{eqnarray} e_{parabola}(\infty) &=& \displaystyle \lim_{ s \to 0 } \frac{s \frac{1}{s^3}}{1+G(s)} = \displaystyle \lim_{ s \to 0 } \frac{1}{s^2+s^2 G(s)} \\ \Rightarrow e_{parabola}(\infty) &=& \displaystyle \lim_{ s \to 0 } \frac{1}{s^2 G(s)} \end{eqnarray} $$

と、パラボラ入力t²u(t)が制御値として与えられた際のフィードバックシステムの定常偏差e_parabola(∞)を求めることが出来ました。