システムを伝達関数で表す：入力、動摩擦力ありの質量、ばね、ダンパーによるシステム

ロボットなどを制御するために伝達関数を用いて、入力に対する出力を表す方法を紹介します。

今回は、質量にばねとダンパーが含まれているモデルに対して、動摩擦力まで考慮した場合のシステムの伝達関数を求める方法を紹介します。

取り扱うシステム

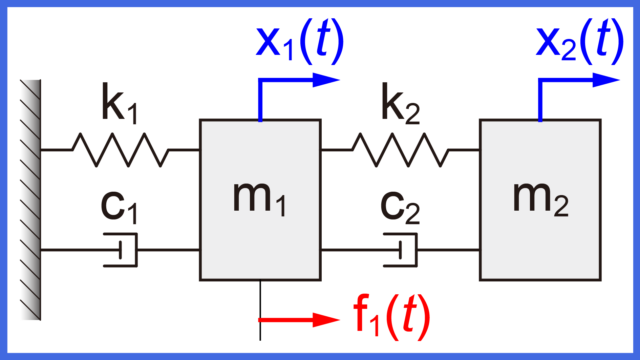
図のように質量（\(m_1\)と\(m_2\)）、ばね（\(k_1\)と\(k_2\)）、ダンパー（\(c_1\)）からなるシステムを取り扱います。

各質量（\(m_1\)と\(m_2\)）には、それぞれ動摩擦力が動摩擦係数（\(\mu_1\)と\(\mu_2\)）と速度（\(\dot{x}_1(t)\)と\(\dot{x}_2(t)\)）との積で掛かります。

このシステムに対し、質量\(m_2\)に右向きに入力\(f(t)\)が与えられた時の質量\(m_1\)の変位\(x_1(t)\)について伝達関数\(G(s)=\frac{X_1(s)}{F(s)}\)を求めていきます。

システム内の各パラメータは、

$$ m_1 = 1 [kg] , m_2 = 2 [kg] $$

$$ k_1 = 4 [N/m] , k_2 = 5 [N/m] $$

$$ c = 3 [N \cdot s/m] $$

$$ \mu_1 = 3 [N \cdot s/m] , \mu_2 = 2 [N \cdot s/m] $$

とします。

運動方程式を求める

それぞれの質量（\(m_1\)と\(m_2\)）について運動方程式を求めていきます。

各質量の運動方程式は、

$$ F = m a $$

の関係式より、

$$ 0 = m_1 \ddot{x}_1(t) + k_1 x_1(t) + \mu_1 \dot{x}_1(t) + k_2 (x_1(t) – x_2(t)) + c (\dot{x}_1(t) – \dot{x}_2(t)) $$

$$ f(t) = m_2 \ddot{x}_2(t) + k_2 (x_2(t) – x_1(t)) + c (\dot{x}_2(t) – \dot{x}_1(t)) + \mu_2 \dot{x}_2(t) $$

と求めることが出来ます。

この運動方程式についてラプラス変換を行い、時間領域\(t\)から周波数領域\(s\)に変換していきます。

ラプラス変換を行う

算出した運動方程式について、各パラメータ値を代入してラプラス変換を行います。

$$ 0 = s^2 X_1(s) + 4 X_1(s) + 3 s X_1(s) + 5 (X_1(s) – X_2(s)) + 3 (s X_1(s) – s X_2(s)) $$

$$ F(s) = 2 s^2 X_2(s) + 5 (X_2(s) – X_1(s)) + 3 (s X_2(s) – s X_1(s)) + 2 s X_2(s) $$

ラプラス変換を行った式について、各変位について整理します。

$$ 0 = \left( s^2 + 6 s + 9 \right) X_1(s) + \left( – 3 s – 5 \right) X_2(s) $$

$$ F(s) = \left( – 3 s – 5 \right) X_1(s) + \left( 2 s^2 + 5 s + 5 \right) X_2(s) $$

この連立方程式を\(X_1(s)\)について解くことで、伝達関数\(G(s)\)を求めていきます。

伝達関数を求める

先程の連立方程式について、1つ目の式から変位\(X_1(s)\)と変位\(X_2(s)\)の関係を求めます。

$$ X_2(s) = \frac{s^2 + 6 s + 9}{3 s + 5} X_1(s) $$

求めた\(X_2(s)\)を\(X_1(s)\)で表した式を2つ目の式に代入し、入力\(F(s)\)と変位\(X_1(s)\)の関係を求めていきます。

$$ F(s) = \left( – 3 s – 5 \right) X_1(s) + \left( 2 s^2 + 5 s + 5 \right) \frac{s^2 + 6 s + 9}{3 s + 5} X_1(s) $$

$$ F(s) = \left( -(3 s + 5) + \frac{( 2 s^2 + 5 s + 5)(s^2 + 6 s + 9)}{3 s + 5} \right) X_1(s) $$

$$ F(s) = \frac{-9s^2-30s-25+2s^4 + 17 s^3 + 53 s^2 + 75 s + 45}{3 s + 5} X_1(s) $$

$$ F(s) = \frac{2s^4 + 17 s^3 + 44 s^2 + 45 s + 20}{3 s + 5} X_1(s) $$

これより、求めたい伝達関数\(G(s)=\frac{X_1(s)}{F(s)}\)は、

$$ G(s) = \frac{X_1(s)}{F(s)} = \frac{3 s + 5}{2s^4 + 17 s^3 + 44 s^2 + 45 s + 20} $$

となることが分かりました。

まとめ

今回は、質量とばねとダンパーが含まれている機械システムについて、動摩擦力まで考慮した場合の伝達関数を求める方法を紹介しました。

システムが複雑になった場合でも、一つずつ求めていくことで、複雑なシステムの伝達関数を求めることが出来ます。