ロボットなどのシステムについて、ブロック線図を用いることで入力と出力の関係を表すことが出来ます。
今回は、複数の伝達要素、加え合わせ点、引き出し点で構成されたブロック線図について、一つの伝達要素（伝達関数）にまとめる方法を紹介します。
ブロック線図の内部信号について詳しくは、こちらの記事を参考にしてください。
取り扱うブロック線図
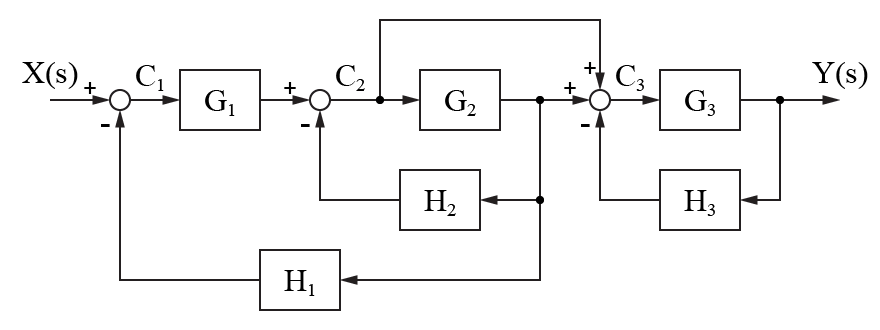
図のように入力X(s)が与えられた時のシステムの出力Y(s)を求めます。
システム内には、伝達要素が6つ、加え合わせ点が3つ、引き出し点が3つ含まれています。
このような複雑なブロック線図を伝達要素が1つだけのブロック線図に変換していきます。
ブロック線図を簡略化することで、複雑なシステムを取り扱いやすくなります。
内部の信号を定義する
複雑なブロック線図について入力を出力の関係を示すために、システムの内部に信号を定義します。
3つの加え合わせ点について、それぞれの出口の信号をC1、C2、C3と定義します。
この定義した内部信号を用いて、入力と出力の関係を表していきます。
出力から入力までの関係を内部信号を用いて示す
出力Y(s)から入力X(s)までの関係を内部信号（C1、C2、C3）を用いて順に表していきます。
$$ \begin{eqnarray} \left\{ \begin{array}{l} Y &=& G_3 C_3 \\ C_3 &=& \left( 1 + G_2 \right) C_2 – G_3 H_3 C_3 \\ C_2 &=& G_1 C_1 – G_2 H_2 C_2 \\ C_1 &=& X – G_2 H_1 C_2 \end{array} \right. \end{eqnarray} $$
これらの4式を連立方程式として、この連立方程式を解くことで出力Y(s)と入力X(s)の関係を求めていきます。
伝達関数を求める
まず、連立方程式の2つ目の式より、
$$ \begin{eqnarray} C_3 &=& \left( 1 + G_2 \right) C_2 – G_3 H_3 C_3 \\ && \Rightarrow C_3 = \frac{1 + G_2}{1 + G_3 H_3} C_2 \end{eqnarray} $$
とC3をC2で表すことが出来ます。
次に、連立方程式の3つ目と4つ目の式より、
$$ C_2 = G_1 C_1 – G_2 H_2 C_2 $$
$$ C_1 = X – G_2 H_1 C_2 $$
$$ \Rightarrow C_2 = G_1 \left( X – G_2 H_1 C_2 \right) – G_2 H_2 C_2 $$
$$ \Rightarrow C_2 = \frac{G_1}{1 + G_1 G_2 H_1 + G_2 H_2} X $$
とC2をXで表すことが出来ます。
これら求めた2式と連立方程式の1つ目の式より、
$$ Y = G_3 C_3 $$
$$ Y = G_3 \frac{1 + G_2}{1 + G_3 H_3} C_2 $$
$$ Y = G_3 \frac{1 + G_2}{1 + G_3 H_3} \frac{G_1}{1 + G_1 G_2 H_1 + G_2 H_2} X $$
と出力Y(s)を入力X(s)で表すことが出来ました。
これより、このシステムの伝達関数G(s)=Y(s)/X(s)は、
$$ G(s) = \frac{Y(s)}{X(s)} = G_3 \frac{1 + G_2}{1 + G_3 H_3} \frac{G_1}{1 + G_1 G_2 H_1 + G_2 H_2} $$
と求めることが出来ます。
この伝達関数を伝達要素として用いることで、複雑だったブロック線図を1つの伝達要素で表すことが出来ました。
まとめ
今回は、ロボットなどのシステムを表すブロック線図について、複雑なブロック線図を1つの伝達要素で構成されたブロック線図に置き換える方法を紹介しました。
次回の記事では、ブロック線図の特性を利用して、複雑なブロック線図を簡単化する手法を紹介したいと思います。
合わせて読みたい記事
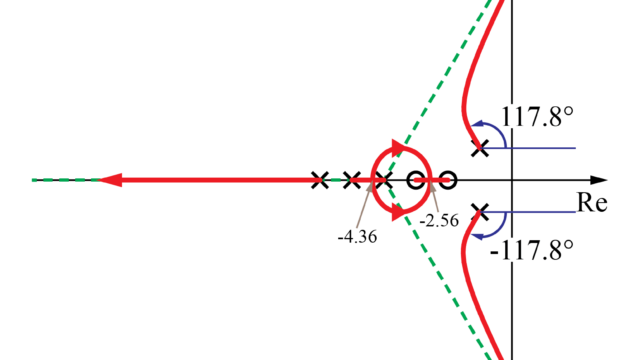
より複雑なブロック線図の例はこちら
ELEGOO Arduinoスターターキット
UNO R3スマートロボットカー
Raspberry Pi 3 Model b+
