摩擦を含んだ2質量系の運動方程式を求める方法

システムの運動方程式や伝達関数の導出は、制御工学においての基本であり、とても重要です。

この運動方程式や伝達関数の算出方法を身につけるためには、いろいろなパターンのシステムを学ぶことが大事だと思います。

以前の記事では、2質量システムの運動方程式の算出方法を紹介しました。

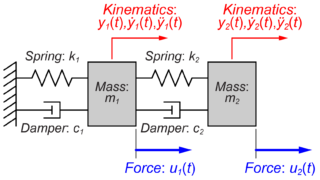
2質量システム（MIMOシステム）の運動方程式を求める MIMO系の状態方程式（状態空間モデル）や伝達関数について、実際に例題を解きながら求めていきたいと思います。 MI...

今回の記事では、摩擦を含む2質量システムの運動方程式と伝達関数を求める流れを紹介します。

Contents

取り扱う2質量システム
運動方程式の導出
まとめ

取り扱う2質量システム

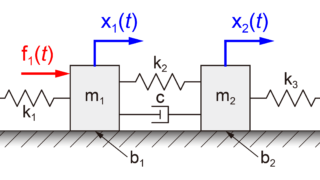
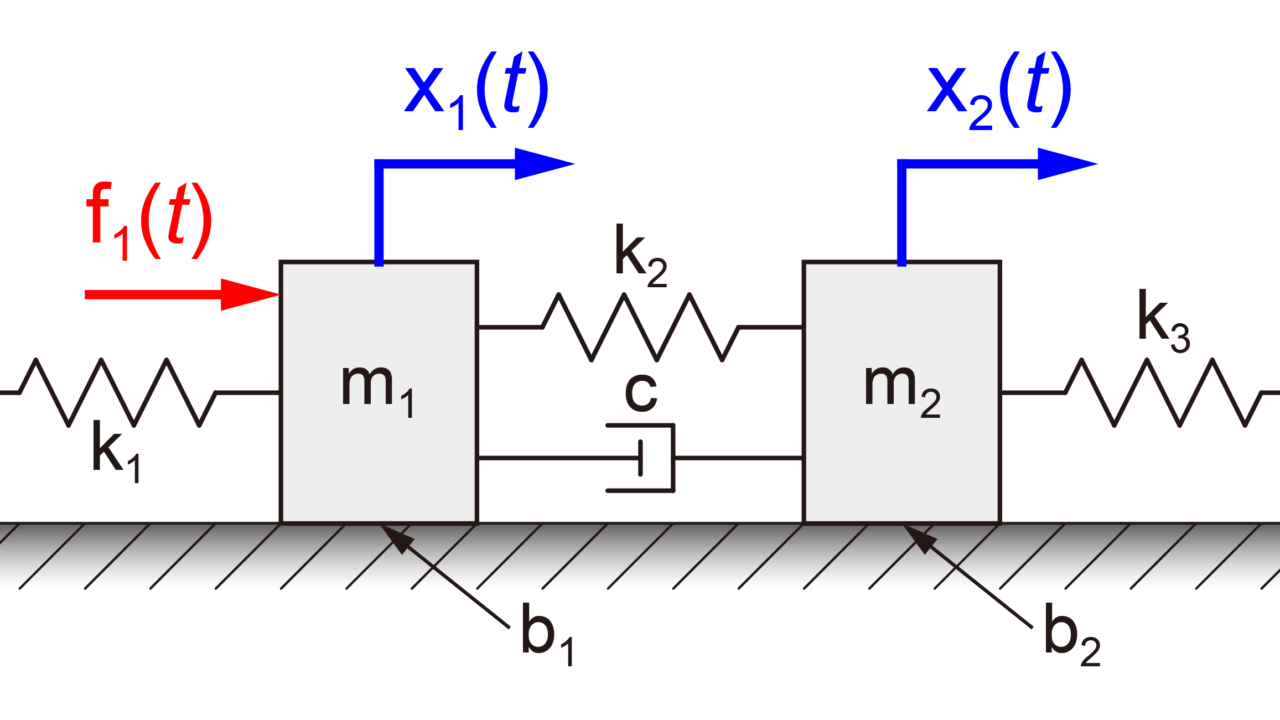
今回の記事では下の図のように、2つの質量が接続されている2質量モデルを取り扱います。

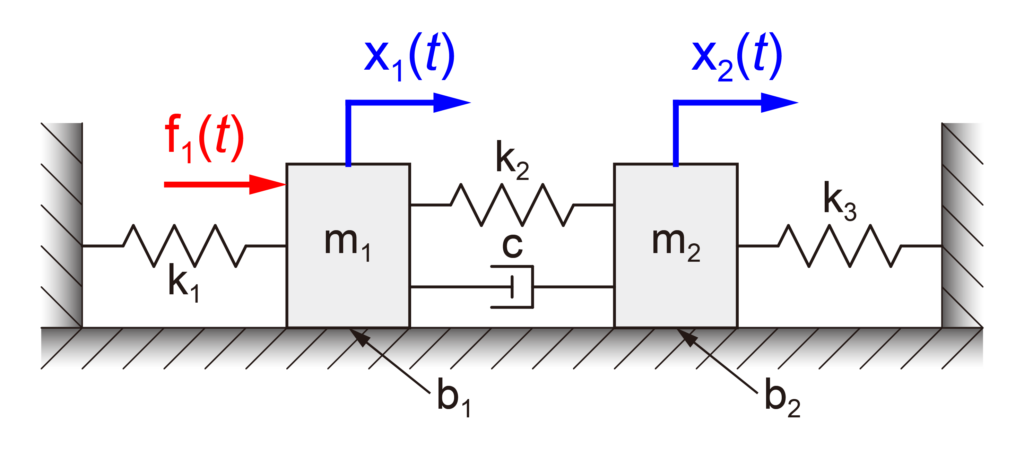
上の図のように、質量m₁に力f₁が加わったときのそれぞれの質量（m₁とm₂）の運動（x₁とx₂）を考えます。

今回は、2つの質量に接続されているばねとダンパーに加えて、各質量にかかる摩擦も考慮します。

この摩擦を含む2自由度系の質量-ばね-ダンパーシステムについて、運動方程式を求めていきます。

運動方程式の導出

2質量システムの運動方程式を求めるために、それぞれの質量にかかる力を考えます。

質量m1の運動方程式

まず始めに、質量m₁について考えます。

質量m₁に影響する力を下図に示します。

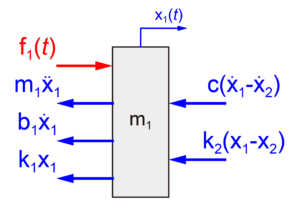
図のように質量m₁には力f₁に加えて、質量m₁と摩擦b₁、ダンパーcとばねk₁とk₂による力が影響します。

また、ダンパーcとばねk₂については、質量m₁の運動のほかに質量m₂の運動を考慮します。

これは、ダンパーcとばねk₂には質量m₁と質量m₂の両方に接続しているからです。

これより、質量m₁に関する力の関係式で表すと

$$ m_1 \ddot{x}_1(t) + b_1 \dot{x}_1(t) + k_1 x_1(t) + c \left( \dot{x}_1(t) – \dot{x}_2(t) \right) + k_2 \left( x_1(t) – x_2(t) \right) = f_1(t) $$

とすることが出来ます。

この式を整理してまとめることで、質量m₁に関する運動方程式

$$ m_1 \ddot{x}_1(t) + \left( b_1 + c \right) \dot{x}_1(t) + \left( k_1 + k_2 \right) x_1(t) – c \dot{x}_2(t) – k_2 x_2(t) = f_1(t) $$

を導出することが出来ました。

質量m2の運動方程式

質量m₁と同様に、質量m₂についても考えます。

下図に質量m₂に影響する力を示します。

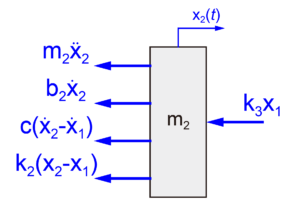
図のように質量m₂には質量m₂と摩擦b₂、ダンパーcとばねk₂とk₃による力が影響します。

先の質量m₁の場合と同様に、ダンパーcとばねk₂については、質量m₂の運動に加えて質量m₁の運動を考慮して算出します。

これらの情報より、質量m₂についての関係式は

$$ m_2 \ddot{x}_2(t) + b_2 \dot{x}_2(t) + c \left( \dot{x}_2(t) – \dot{x}_1(t) \right) + k_2 \left( x_2(t) – x_1(t) \right) + k_3 x_2(t) = 0 $$

と表すことが出来ます。

この式を整理してまとめることで、質量m₂に関する運動方程式

$$ m_2 \ddot{x}_2(t) + \left( b_2 + c \right) \dot{x}_2(t) + \left( k_2 + k_3 \right) x_2(t) – c \dot{x}_1(t) – k_2 x_1(t) = 0 $$

を求めることが出来ました。

2質量系の運動方程式

これまでに求めた各質量の運動方程式より、今回の記事で取り扱っているシステムの運動方程式は、

$$ \begin{eqnarray} \left\{ \begin{array}{l} m_1 \ddot{x}_1(t) + \left( b_1 + c \right) \dot{x}_1(t) + \left( k_1 + k_2 \right) x_1(t) – c \dot{x}_2(t) – k_2 x_2(t) &=& f_1(t) \\ m_2 \ddot{x}_2(t) + \left( b_2 + c \right) \dot{x}_2(t) + \left( k_2 + k_3 \right) x_2(t) – c \dot{x}_1(t) – k_2 x_1(t) &=& 0 \end{array} \right. \end{eqnarray} $$

となることが分かりました。

ちなみに、質量m₂にも力f₂が加わる場合は、運動方程式の第2式の右辺の0がf₂に代わります。