システムが伝達関数として与えられた場合に、その伝達関数からボード線図を書く方法を紹介しています。
これまでの記事では、
が伝達関数として与えられた場合のボード線図の書き方を紹介しました。
今回は、1次遅れ要素が伝達関数で与えられた場合について、ボード線図の書き方を紹介していきたいと思います。
1次遅れ要素の伝達関数
今回は、システムの伝達関数\(G(s)\)として
$$ G(s) = \frac{1}{s + a} $$
のように、1次遅れ要素が与えられた場合についてボード線図を求めていきます。

ボード線図はシステムの定常状態での関係を示すため、この伝達関数内の複素数\(s\)を
$$ s = j \omega $$
と置き換えると、与えられた1次遅れ要素を表す伝達関数\(G(s)\)は
$$ \begin{eqnarray} G(j \omega) &=& \frac{1}{j \omega + a} \\ &=& \frac{1}{a \left(j \frac{\omega}{a} + 1 \right)} \end{eqnarray} $$
と書き換えることが出来ます。
ゲインと位相を算出
実際に1次遅れ要素に対するボード線図を書くため、周波数\(\omega\)が小さい場合と大きい場合に場合分けして、それぞれのゲインと位相を求めていきます。
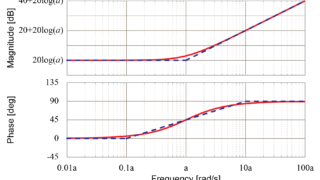
基本的なゲインと位相の求め方の流れは1次進み要素の場合と同様です。
周波数が十分に小さい場合
入力信号の周波数\(\omega\)が小さい場合について、ゲインと位相を求めていきます。
周波数\(\omega\)が十分に小さい場合、伝達関数\(G(j \omega)\)
$$ G(j \omega) =\frac{1}{ a \left(j \frac{\omega}{a} + 1 \right) } $$
の中に含まれる式について
$$ \begin{eqnarray} \omega \ll a \\ \Rightarrow \frac{\omega}{a} = 0 \end{eqnarray} $$
が成り立ちます。
そのため、1次遅れ要素の伝達関数\(G(j \omega)\)は
$$ G(j \omega) \approx \frac{1}{a} $$
と書くことが出来ます。
この伝達関数\(G(j \omega)\)より、ゲインは
$$ \begin{eqnarray} Magnitude &=& 20 \log M = 20 \log |G(j \omega)| \\ &=& 20 \log \frac{1}{a} \ [dB] \\ &=& -20 \log a \ [dB] \end{eqnarray}$$
と求めることが出来ます。
また、伝達関数\(G(j \omega)\)は正の実数のみで構成されているので
$$ Phase = 0 \ [^{\circ}] $$
となります。
周波数が十分に大きい場合
同様に、入力信号の周波数\(\omega\)が小さい場合について、ゲインと位相を求めていきます。
周波数\(\omega\)が十分に大きい場合、伝達関数\(G(j \omega)\)に含まれる式について
$$ \begin{eqnarray} \omega \gg a \\ \Rightarrow \frac{\omega}{a} \gg 1 \end{eqnarray} $$
が成り立ちます。
よって、伝達関数\(G(j \omega)\)を
$$ \begin{eqnarray} G(j \omega) &\approx& \frac{1}{j \omega} \\ &=& -j \frac{1}{\omega} \end{eqnarray} $$
と表すことが出来ます。
この伝達関数\(G(j \omega)\)より、ゲインを求めると
$$ \begin{eqnarray} Magnitude &=& 20 \log M = 20 \log |G(j \omega)| \\ &=& 20 \log \frac{1}{\omega} \ [dB] \\ &=& -20 \log \omega \ [dB] \end{eqnarray}$$
となる事が分かります。
ここで、伝達関数\(G(j \omega)\)は負の虚数のみで構成されているので
$$ Phase = -90 \ [^{\circ}] $$
となります。
漸近線近似によるボード線図
算出したゲインと位相を表す式から、1次遅れ要素のボード線図を直線の漸近線を用いて近似を行います。
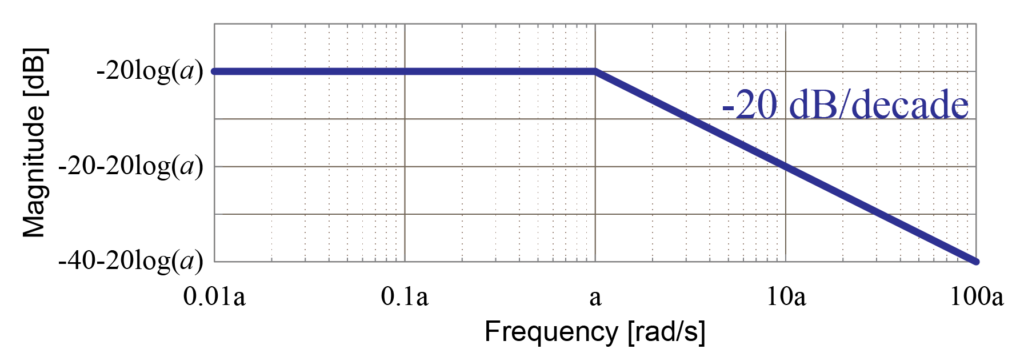
ゲイン線図
周波数\(\omega\)が小さい場合は
$$ Magnitude = – 20 \log a \ [dB] $$
となり、傾き\(0\)の一定値の直線で近似することが出来ます。
そして周波数\(\omega\)が大きくなると
$$ Magnitude = – 20 \log \omega \ [dB] $$
のように、積分要素の場合と同様に右下がりの直線で近似が出来ます。
ここで2つの近似が変化する周波数\(\omega\)を1次遅れ要素\(\frac{1}{s+a}\)に含まれている\(a\)とすることで、図のように直線の漸近線を用いたゲイン線図の近似を行うことが出来ます。
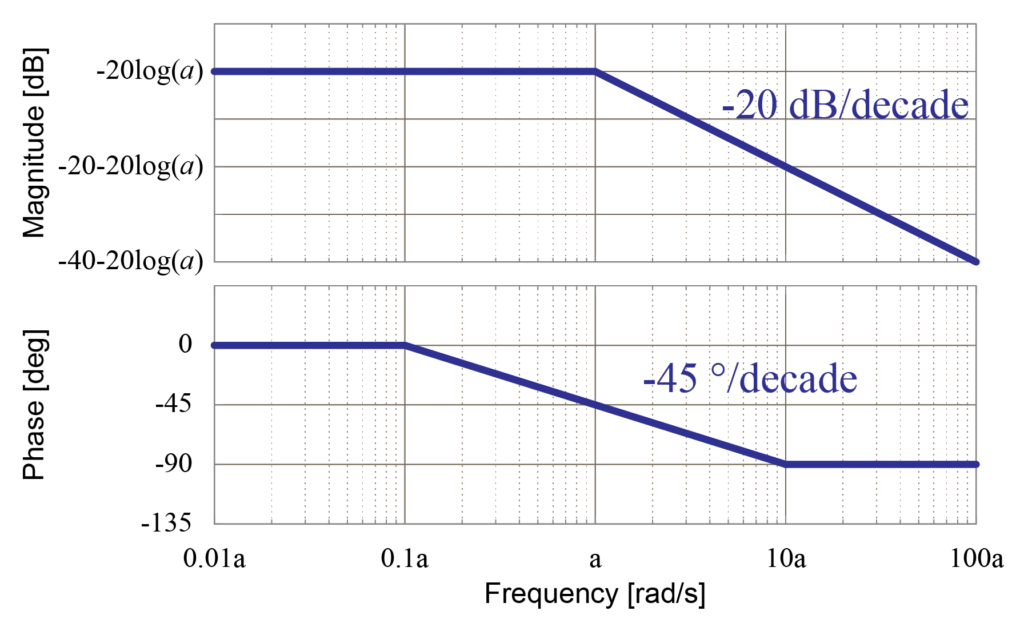
位相線図
周波数\(\omega\)が小さい場合に位相は
$$ Phase = 0 \ [^{\circ}] $$
となります。
また、周波数\(\omega\)が大きくなると
$$ Phase = -90 \ [^{\circ}] $$
と表されます。
さらに、周波数\(\omega\)が
$$ \omega = a $$
の場合の1次進み要素を考えると、伝達関数\(G(j \omega) \)は
$$ G(j \omega) = \frac{1}{j a + a} $$
となります。
この式を整理すると
$$ \begin{eqnarray} \frac{1}{j a + a} &=& \frac{-(j a + a)}{(j a + a)(-j a + a)} \\ &=& \frac{a – ja}{a^2+a^2} \\ &=& \frac{1 – j1}{\sqrt{2} a} \end{eqnarray} $$
と表すことが出来ます。
よって、この時の位相は
$$ Phase = – 45 \ [^{\circ}] $$
となる事が分かります。
ここで、位相線図に関して十分に小さい周波数を0.1倍の
$$ \omega = \frac{1}{10} a = 0.1 a $$
とし、十分に大きい周波数を10倍の
$$ \omega = 10 a $$
とします。
この2つの周波数の地点を直線で結ぶことで、漸近線を用いた位相線図の近似を行うことが出来ます。
この時、周波数\(\omega\)が\(a\)の地点では、先に求めた通り位相が\(-45^{\circ}\)になっていることが分かります。
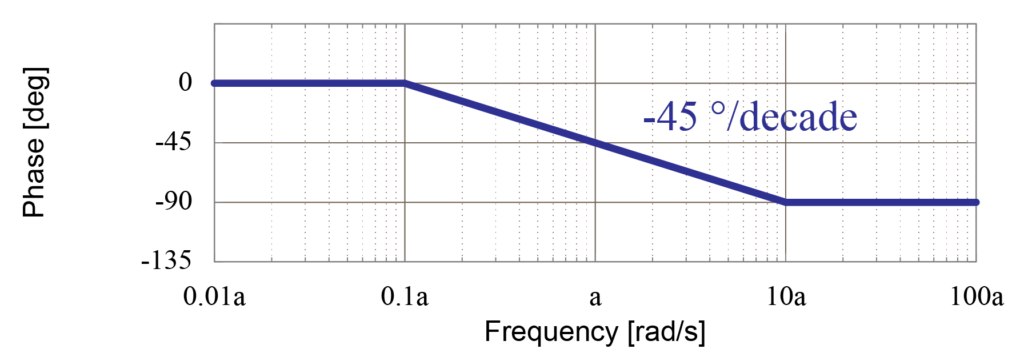
漸近線近似と実際のボード線図との比較
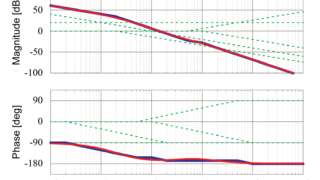
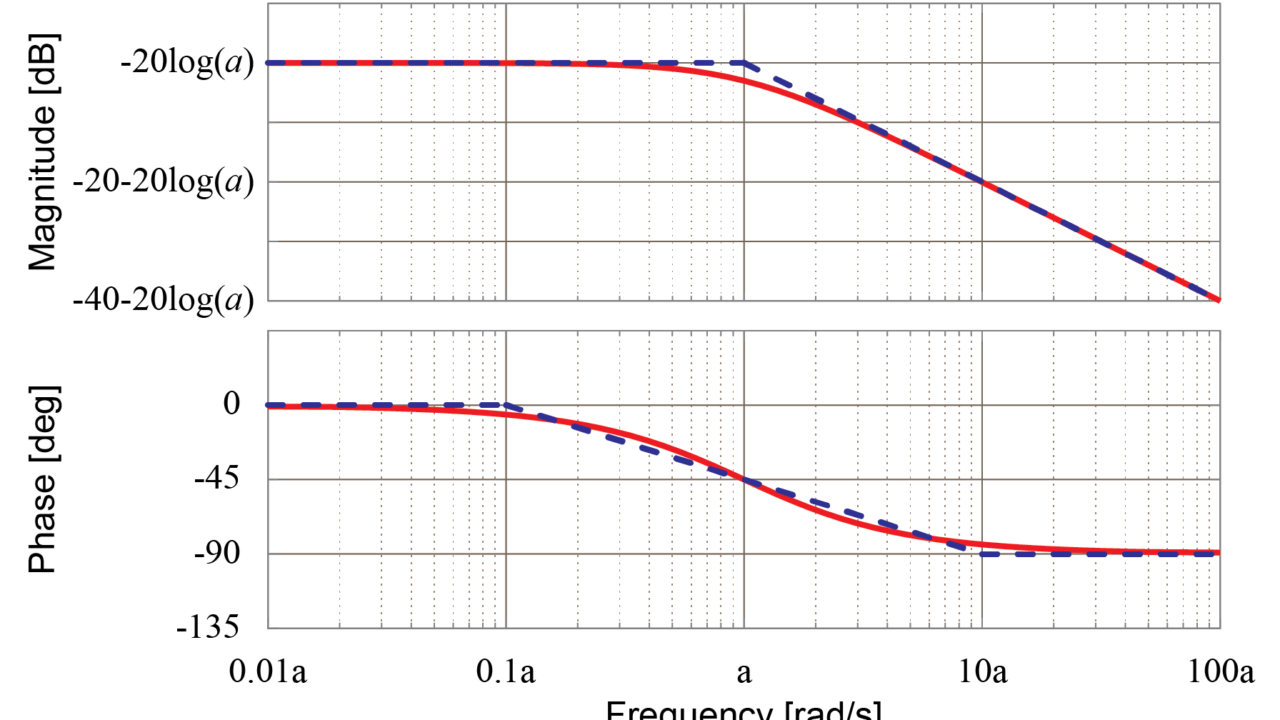
先ほど求めた漸近線で近似したボード線図と、実際のボード線図を比較してみます。
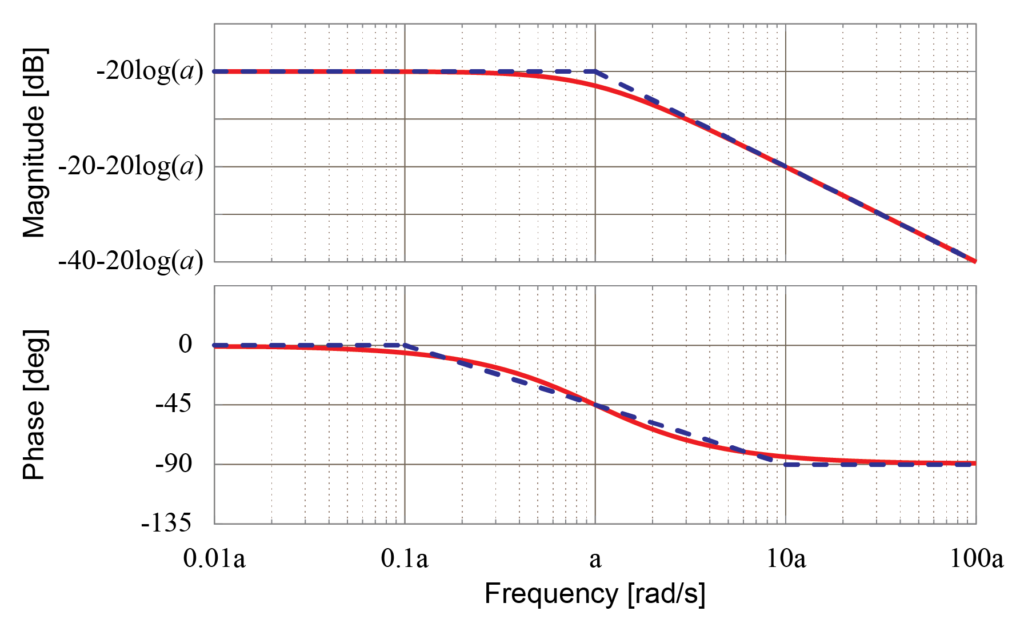
比較したボード線図より、漸近線近似(青の点線)と実際のボード線図(赤の実践)は、ほとんど同じとなっていることが分かります。
まとめ
今回は、1次遅れ要素が伝達関数として与えられた場合について、漸近線を用いた近似によりボード線図を書く方法を紹介しました。
実際に求めたボード線図との比較した結果、今回の記事で紹介している漸近線近似の手法は、1次遅れ要素のボード線図を表すために有効だと分かりました。
次回の記事では、2次進み要素や2次遅れ要素が伝達関数として与えられた場合について、実際にボード線図を書く方法を紹介していきたいと思います。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
