MIMO系システムの状態空間モデルから伝達関数行列を求める

MIMO系の状態空間モデル（状態方程式）から伝達関数を求める方法を紹介します。

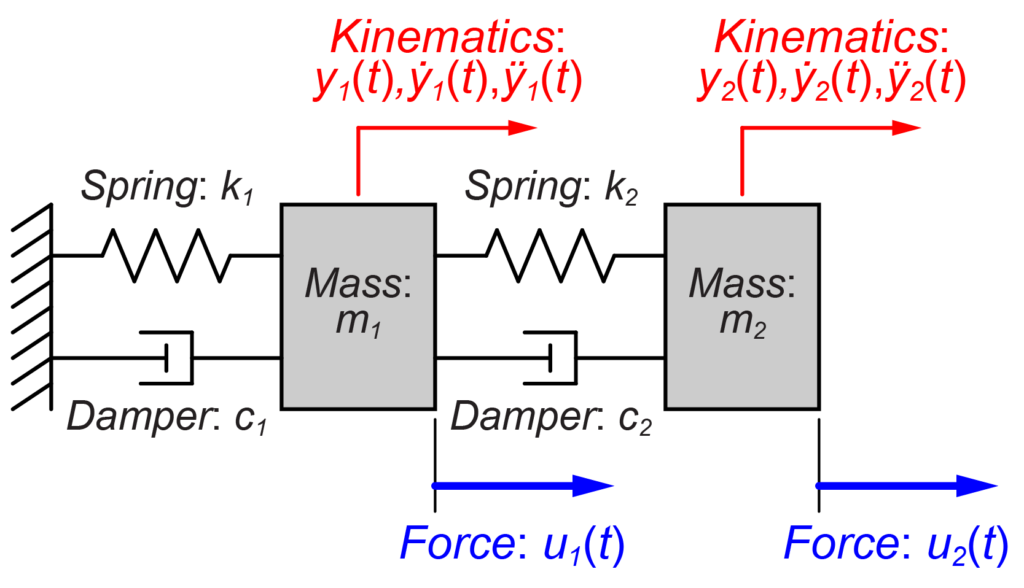
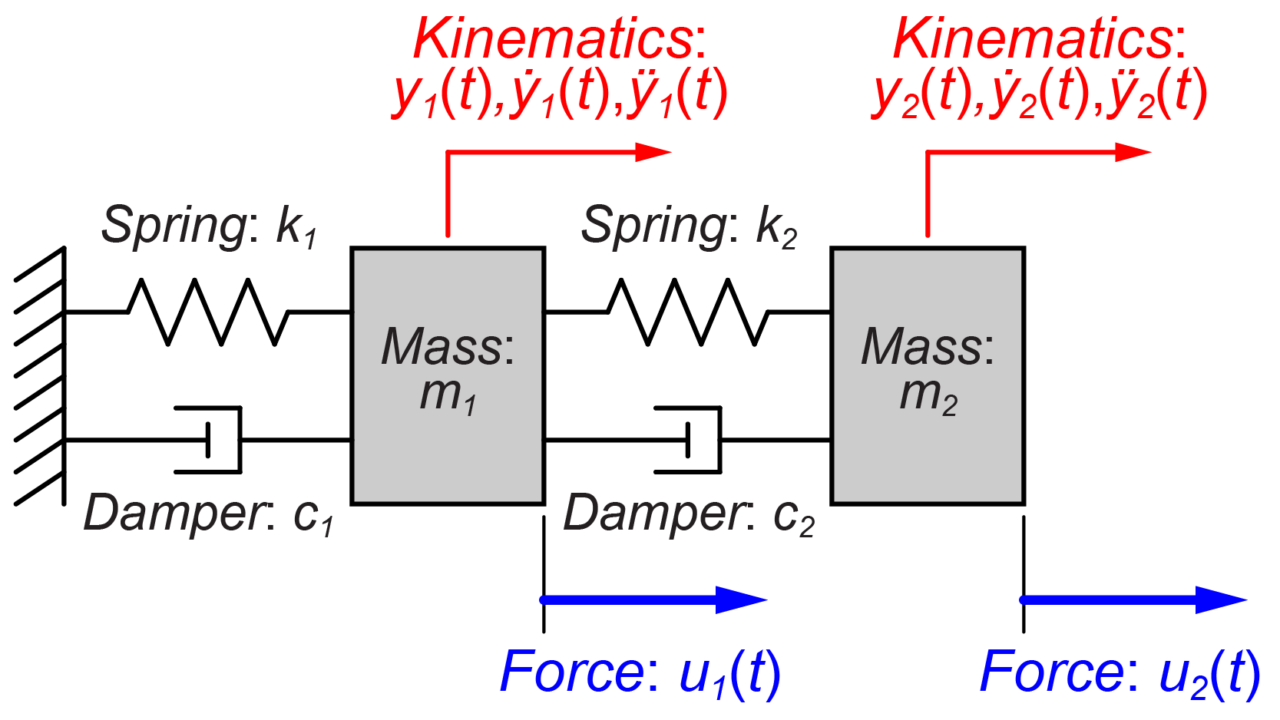
今回もMIMOシステムの例として2質量系モデルを扱います。

このMIMO系モデルの状態空間モデルについては、こちらの記事を参考にしてください。

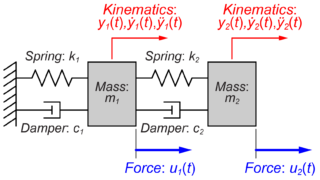
状態方程式で2質量システム（MIMOシステム）を表す2質量システムを例に、実際にMIMO系システムの運動方程式から状態方程式を求める方法を紹介します。...

このモデルの伝達関数をラプラス変換を用いて求める方法は、こちらの記事を参考にしてください。

伝達関数でMIMOシステム（2質量系）を表すMIMOシステムの例として2質量系モデルを用いて、実際に線形微分方程式（運動方程式）から伝達関数を求める方法を紹介します。...

Contents

状態空間モデルと伝達関数の関係
状態空間モデルから伝達関数の算出
まとめ

状態空間モデルと伝達関数の関係

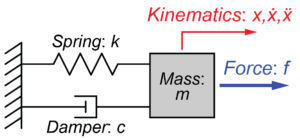
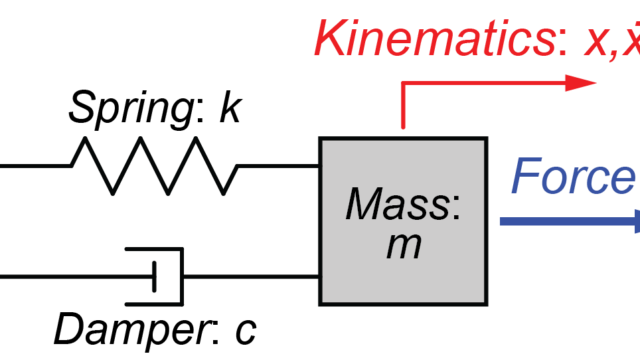
以前の記事で、SISO系の質量-ばね-ダンパーシステムについて、状態空間モデルと伝達関数は、

$$ G(s) = \frac{Y(s)}{U(s)} = \boldsymbol{ C } \left( s \boldsymbol{ I } – \boldsymbol{ A } \right)^{-1} \boldsymbol{ B } + D $$

と表すことが出来ると紹介しました。

このSISO系で用いた関係式はMIMO系でも同様に用いることが出来ます。

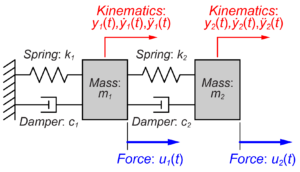
今回扱っている2質量システムの状態空間モデルの各行列は、

$$ \boldsymbol{A} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ – \frac{k_1+k_2}{m_1} & – \frac{c_1+c_2}{m_1} & \frac{k_2}{m_1} & \frac{c_2}{m_1} \\ 0 & 0 & 0 & 1 \\ \frac{k_2}{m_2} & \frac{c_2}{m_2} & – \frac{k_2}{m_2} & – \frac{c_2}{m_2} \end{bmatrix} $$

$$ \boldsymbol{B} = \begin{bmatrix} 0 & 0 \\ \frac{1}{m_1} & 0 \\ 0 & 0 \\ 0 & \frac{1}{m_2} \end{bmatrix} $$

$$ \boldsymbol{C} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} $$

$$ \boldsymbol{D} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} $$

となります。

今回の2質量モデルは、2入力2出力システムなので、算出した伝達関数は$2 \times 2$の行列になります。

状態空間モデルから伝達関数の算出

実際に値を入れて計算していきます。

$$ \boldsymbol{G(s)} = \frac{\boldsymbol{Y(s)}}{\boldsymbol{U(s)}} = \boldsymbol{ C } \left( s \boldsymbol{ I } – \boldsymbol{ A } \right)^{-1} \boldsymbol{ B } + \boldsymbol{ D } $$

$$ = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \left( s \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} – \begin{bmatrix} 0 & 1 & 0 & 0 \\ – \frac{k_1+k_2}{m_1} & – \frac{c_1+c_2}{m_1} & \frac{k_2}{m_1} & \frac{c_2}{m_1} \\ 0 & 0 & 0 & 1 \\ \frac{k_2}{m_2} & \frac{c_2}{m_2} & – \frac{k_2}{m_2} & – \frac{c_2}{m_2} \end{bmatrix} \right)^{-1} \begin{bmatrix} 0 & 0 \\ \frac{1}{m_1} & 0 \\ 0 & 0 \\ 0 & \frac{1}{m_2} \end{bmatrix} + \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} $$

$$ = \begin{bmatrix} \frac{m_2 s^2 + c_2 s + k_2}{ \left( m_1 s^2 + c_1 s + k_1 \right) \left( m_2 s^2 + c_2 s + k_2 \right) + m_2 s^2 \left( c_2 s + k_2 \right) } & \frac{c_2 s + k_2}{ \left( m_1 s^2 + c_1 s + k_1 \right) \left( m_2 s^2 + c_2 s + k_2 \right) + m_2 s^2 \left( c_2 s + k_2 \right) } \\ \frac{c_2 s + k_2}{ \left( m_1 s^2 + c_1 s + k_1 \right) \left( m_2 s^2 + c_2 s + k_2 \right) + m_2 s^2 \left( c_2 s + k_2 \right) } & \frac{m_1 s^2 + \left(c_1+c_2\right) s + \left(k_1+k_2\right)}{ \left( m_1 s^2 + c_1 s + k_1 \right) \left( m_2 s^2 + c_2 s + k_2 \right) + m_2 s^2 \left( c_2 s + k_2 \right) } \end{bmatrix} $$

この伝達関数行列は、以前の記事でラプラス変換から導出した場合との同じになります。