制御工学を学ぶ上で、システムの運動を理解することは重要です。
様々な機械システムの基本として、1つの質量にばねとダンパーが接続された1自由度の質量-ばね-ダンパーシステムがあります。
今回の記事では、この1自由度振動系を取り扱うために必要となるシステムの運動方程式、伝達関数、状態方程式を紹介します。
1自由度振動系モデル
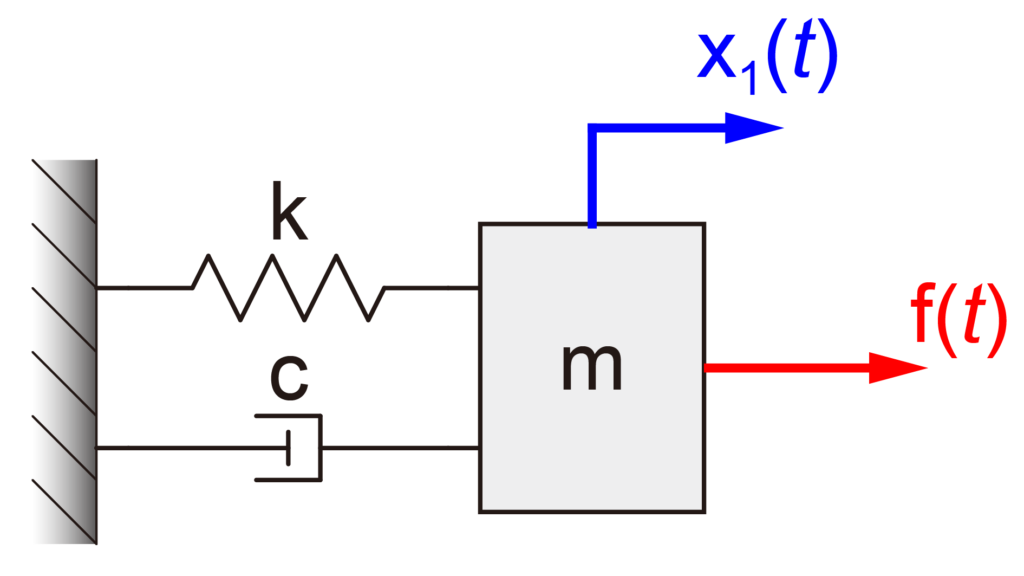
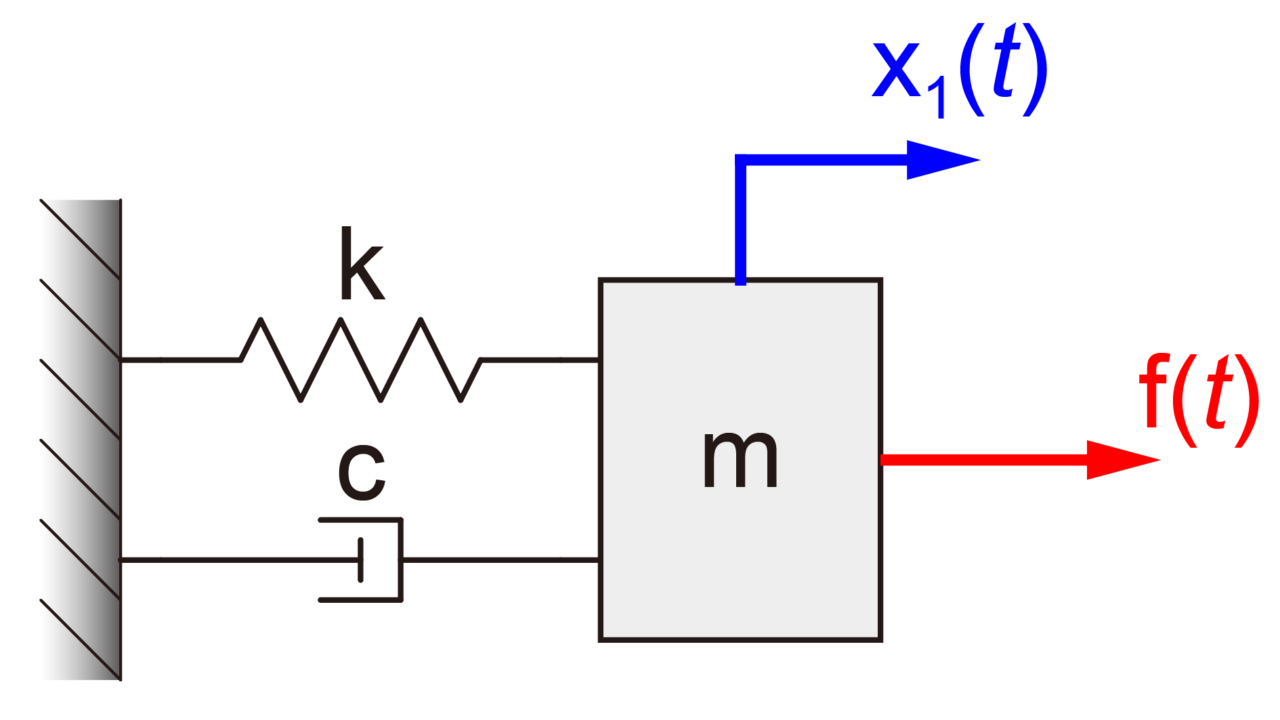
今回の記事では、下の図のように質量mがばねkとダンパーcにより壁に接続された1自由度のモデルを取り扱います。
この様に質量とばねとダンパーで構成されたシステムを質量-ばね-ダンパーシステムと言います。
この1自由度の質量-ばね-ダンパーモデルについて、運動方程式と伝達関数、状態方程式を紹介します。
詳しい算出方法は各項目のリンクを参照してください。
1自由度系の運動方程式
運動方程式とは、運動の法則を表した数式のことを言います。
入力fと各要素(質量m、ダンパーc、ばねk)による力の関係式を微分方程式の形で求めることで算出できます。
1自由度振動系の運動方程式は下記の数式で表されます。
$$ m \ddot{x}(t) + c \dot{x}(t) + k x(t) = f(t) $$
この運動方程式(微分方程式)を解くことで、入力に対する質量の運動(変位)を求めることが出来ます。
運動方程式については、こちらの記事も参考にしてください。

1自由度系の伝達関数
伝達関数とは、システムの入力を出力に変換する関数のことを言います。
ラプラス変換により運動の法則より得られた式を周波数領域に変換し、出力信号X(s)(質量の変位x(t))を入力信号U(s)(力f(t))で割ることで求められます。
1自由度振動系の伝達関数は下記の数式で表されます。
$$ G(s) = \frac{X(s)}{U(s)} = \frac{1}{m s^2 + c s + k} $$
この伝達関数を用いることで、システムの応答特性や安定性を求めることが出来ます。
また、逆ラプラス変換により伝達関数を時間領域に変換することで、システムの運動を求めることが出来ます。
伝達関数については、こちらの記事も参考にしてください。

1自由度系の状態方程式
状態方程式とは、入出力関係に加えて内部状態を表した数式のことを言います。
内部状態を表す状態変数x(t)とdx(t)/dtによる状態ベクトルX(=[x(t),dx(t)/dt]T)と、入力f(t)による入力ベクトルU(=f(t))との関係を1階微分方程式で表すことで求められます。
1自由度振動系の状態方程式は下記の数式で表されます。
$$ \boldsymbol{ \dot{ X } } = \begin{bmatrix} 0 & 1 \\ – \frac{k}{m} & – \frac{c}{m} \end{bmatrix} \boldsymbol{ X } + \begin{bmatrix} 0 \\ \frac{1}{m} \end{bmatrix} \boldsymbol{ X } $$
この状態方程式を解くことで、システムの運動の様子を得ることが出来ます。
また、状態方程式を用いることで、多入力多出力のシステムを取り扱うことが出来ます。
状態方程式については、こちらの記事も参考にしてください。
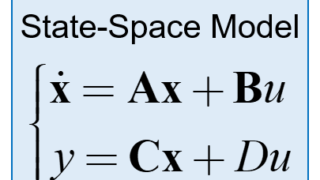
まとめ
今回は1自由度振動系の運動方程式、伝達関数、状態方程式について紹介しました。
1自由度系をしっかりと理解することで、より複雑な2自由度系や3自由度系などシステムを取り扱うことが出来るようになります。
























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
