複数の質量からなるモデルを用いて、このシステムの振動を算出する方法を紹介します。
1つの質量からなるモデルの振動については、こちらの記事を参考にしてください。
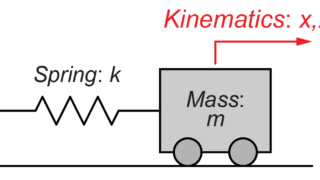
2質量モデル
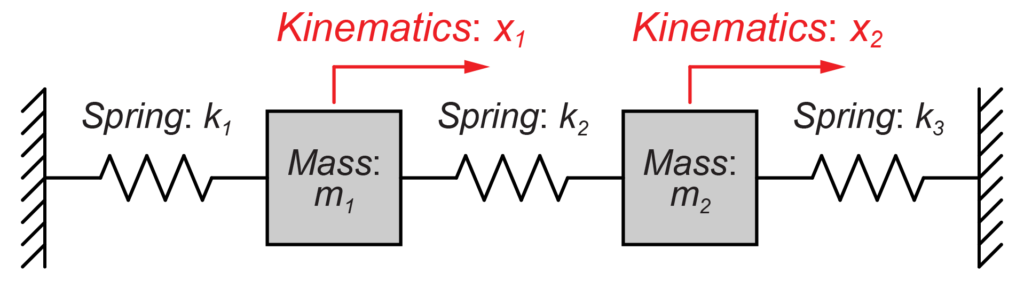
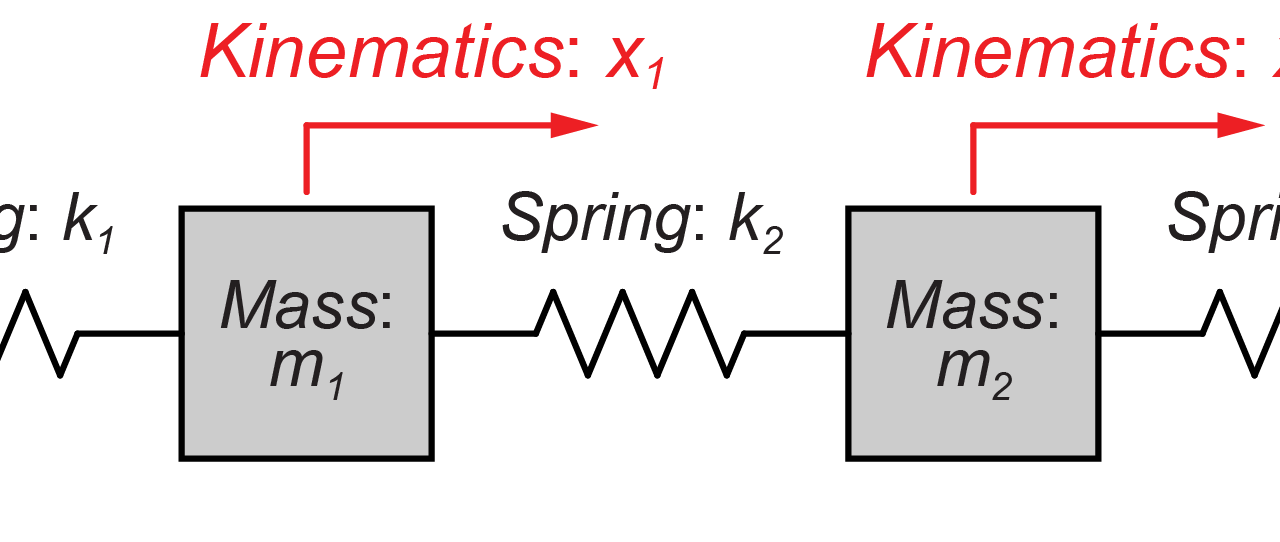
今回は、図のように2質量(m1とm2)がそれぞればね(k1、k2、k3)によって壁と互いに接続されているモデルを扱います。
システム内に質量が2つありますが、質量が1つの場合と同様に、ラグランジュ方程式を用いて運動方程式を求めていきます。
2質量モデルの各エネルギー
ラグランジュ方程式を用いて運動方程式を求めるために、システムの運動エネルギーと位置エネルギーを求めていきます。
運動エネルギー
質量m1の運動エネルギーKE1は、質量m1とその速度\(\dot{x}_1\)の2乗より、
$$ {KE}_1 = \frac{1}{2} m_1 {\dot{x}_1}^2 $$
と表すことが出来ます。
同様に、質量m2の運動エネルギーKE2は、質量m2とその速度\(\dot{x}_2\)の2乗より、
$$ {KE}_2 = \frac{1}{2} m_2 {\dot{x}_2}^2 $$
と表すことが出来ます。
よって、システム全体の運動エネルギーKEは、2つの質量の運動エネルギーの計より、
$$ KE = {KE}_1 + {KE}_2 $$
$$ = \frac{1}{2} m_1 {\dot{x}_1}^2 + \frac{1}{2} m_2 {\dot{x}_2}^2 $$
となります。
位置エネルギー
位置エネルギーPEはシステム内のばね(k1、k2、k3)による位置エネルギーの計で求めることが出来ます。
ばねk1による位置エネルギーPE1は、ばねk1とその変位\(x_1\)の2乗より、
$$ {PE}_1 = \frac{1}{2} k_1 {x_1}^2 $$
と表すことが出来ます。
同様に、ばねk3による位置エネルギーPE3は、ばねk3とその変位\(x_2\)の2乗より、
$$ {PE}_3 = \frac{1}{2} k_3 {x_2}^2 $$
と表すことが出来ます。
2質量間のばねk2による位置エネルギーは、ばねk2とその変位(x2 – x1)の2乗より、
$$ {PE}_2 = \frac{1}{2} k_2 \left(x_2 – x_1\right)^2 $$
となります。
よって、システム全体の位置エネルギーPEは、各位置エネルギーの計より、
$$ PE = {PE}_1 + {PE}_2 + {PE}_3 $$
$$ = \frac{1}{2} k_1 {x_1}^2 + \frac{1}{2} k_2 \left(x_2 – x_1\right)^2 + \frac{1}{2} k_3 {x_2}^2 $$
となります。
2質量モデルのラグランジュ方程式
複数の質量を含むモデルのラグランジュ方程式は、
$$ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}_i} KE \right) + \frac{\partial}{\partial x_i} PE = 0$$
と表すことが出来ます。
今回のシステムにおけるxiは、x1とx2です。
このラグランジュ方程式に各エネルギーの値を代入して解いていきます。
x1について
各エネルギーをラグランジュ方程式に代入した関係式をx1について解いていきます。
$$ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}_1} \left(\frac{1}{2} m_1 {\dot{x}_1}^2 + \frac{1}{2} m_2 {\dot{x}_2}^2\right) \right) $$
$$ + \frac{\partial}{\partial x_1} \left(\frac{1}{2} k_1 {x_1}^2 + \frac{1}{2} k_2 \left(x_2 – x_1\right)^2 + \frac{1}{2} k_3 {x_2}^2\right) = 0$$
$$ \Rightarrow m_1 \ddot{x}_1(t) + k_1 x_1(t) – k_2 \left(x_2 – x_1\right) = 0 $$
よって、x1についての運動方程式は、
$$ m_1 \ddot{x}_1(t) + \left(k_1 + k_2\right) x_1(t) – k_2 x_2(t) = 0 $$
となりました。
x2について
同様に、各エネルギーをラグランジュ方程式に代入した関係式をx2について解いていきます。
x1について求めた時と同様に、x2についての運動方程式は、
$$ m_2 \ddot{x}_2(t) – k_2 x_1(t)+ \left(k_2 + k_3\right) x_2(t) = 0 $$
となります。
2質量モデルの運動方程式
先程求めた2式から、今回の2質量モデルの運動方程式は、
$$ \begin{eqnarray} \left\{ \begin{array}{l} m_1 \ddot{x}_1(t) + \left(k_1 + k_2\right) x_1(t) – k_2 x_2(t) = 0 \\ m_2 \ddot{x}_2(t) – k_2 x_1(t)+ \left(k_2 + k_3\right) x_2(t) = 0 \end{array} \right. \end{eqnarray} $$
となりました。
この2式を行列式として1式にまとめると、
$$ \begin{bmatrix} m_1 & 0 \\ 0 & m_2 \end{bmatrix} \begin{bmatrix} \ddot{x_1} \\ \ddot{x_2} \end{bmatrix} + \begin{bmatrix} k_1+k_2 & -k_2 \\ -k_2 & k_2+k_3 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$
と表すことが出来ます。
まとめ
今回は、2質量モデルを例にシステムの運動(振動)を算出する方法を紹介しました。
次回は、求めた2質量モデルの運動方程式から振動の様子(振幅や周期)を求める方法を紹介したいと思います。
























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
