ロボットなどのシステムを表した複雑なブロック線図について、簡単化するために必要な知識を紹介していきます。
今回は第4回目です。
過去の記事はこちら。


今回は、加え合わせ点と伝達要素の関係についての知識を、数式を用いながら証明していきます。
伝達要素と加え合わせ点
伝達要素を用いることで、入力された信号を伝達要素(伝達関数)に応じて出力信号に変換することが出来ます。
加え合わせ点を用いることで、信号の足し算や引き算を行うことが出来ます。
この伝達要素と加え合わせ点について、ブロック線図の簡単化のために必要な特性を紹介していきます。
伝達要素を加え合わせ点の後から前に移動
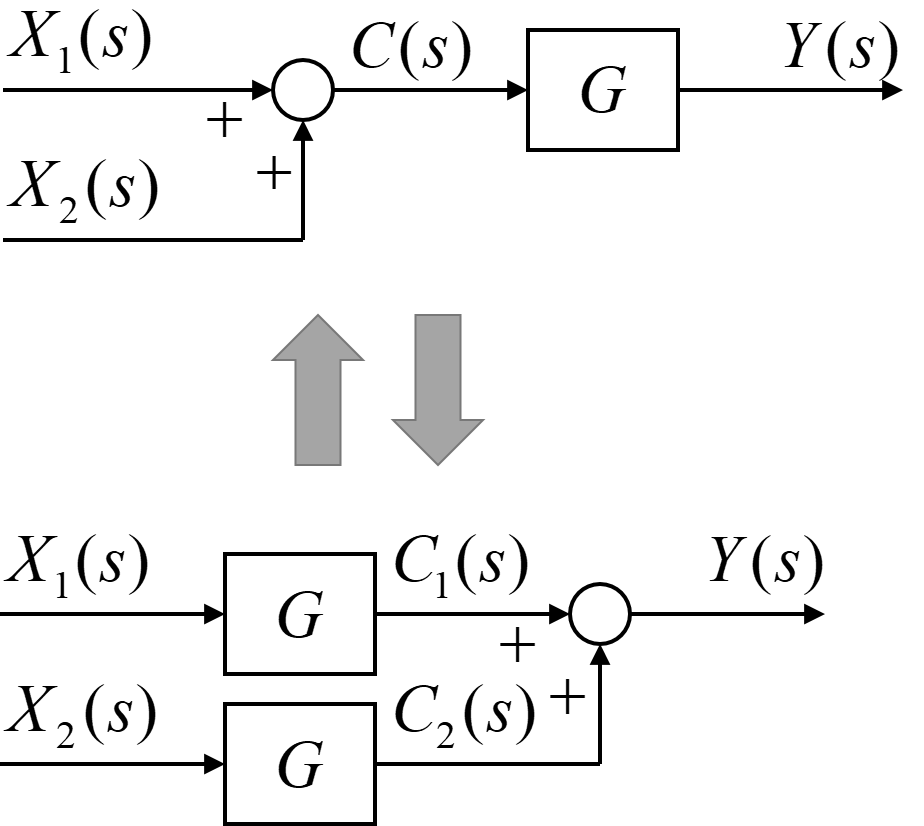
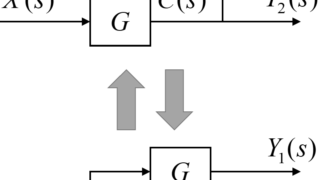
引き出し点の後にある伝達要素は、加え合わせ点で足し合わされる前の両方の信号に伝達要素を掛けることで、加え合わせ点の後から前に移動させることが出来ます。
2つの入力信号をそれぞれ\(X_1(s)\)と\(X_2(s)\)、出力信号を\(Y(s)\)とします。
まず上の図のように、2つの入力信号\(X_1(s)\)と\(X_2(s)\)が加え合わせ点で足し合わされた後に伝達要素\(G\)を通る場合の出力信号\(Y(s)\)を考えます。
加え合わせ点で足し合わされた内部信号\(C(s)\)は、入力信号\(X_1(s)\)と\(X_2(s)\)より、
$$ C(s) = X_1(s) + X_2(s) $$
と表すことが出来ます。
出力信号\(Y(s)\)は、内部信号\(C(s)\)と伝達要素\(G\)を用いて、
$$ Y(s) = G C(s) $$
となります。
よって、出力信号(\(Y(s)\))と入力信号(\(X_1(s)\)と\(X_2(s)\))の関係は、
$$ Y(s) = G \left( X_1(s) + X_2(s) \right) $$
と表すことが出来ます。
つぎに下の図のように、入力信号\(X_1(s)\)と\(X_2(s)\)が伝達要素\(G\)を通った後、加え合わせ点よって足し合わされ、出力信号\(Y(s)\)となる場合を考えます。
入力信号\(X_1(s)\)と\(X_2(s)\)はそれぞれ伝達要素\(G\)によって、内部信号\(C_1(s)\)と\(C_2(s)\)に変換されます。
$$ C_1(s) = G X_1(s) $$
$$ C_2(s) = G X_2(s) $$
出力信号\(Y(s)\)は、2つの内部信号\(C_1(s)\)と\(C_2(s)\)が加え合わせ点で足し合わされるため、
$$ Y(s) = C_1(s) + C_2(s) $$
となります。
よって、出力信号(\(Y(s)\))は入力信号(\(X_1(s)\)と\(X_2(s)\))を用いて、
$$ Y(s) = G \left( X_1(s) + X_2(s) \right) $$
と求めることが出来ます。
これより、組み合わせ点の後にある伝達要素(上図)を組み合わせ点の前に移動させた場合(下図)も出力信号は同じになることが分かりました。
伝達要素を引き出し点の後から前に移動
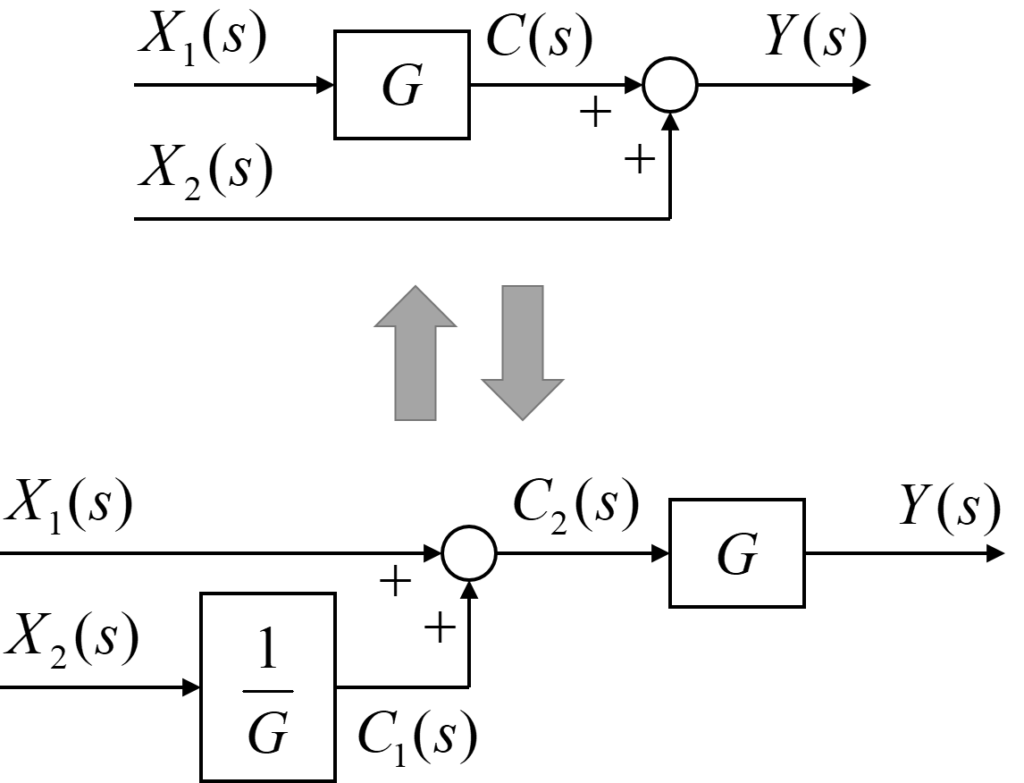
加え合わせ点の前にある伝達要素は、加え合わせ点の後に移動し、かつもう一方の加え合わされる信号に伝達要素の逆数を掛けることで、組み合わせ点の前から後に移動させることが出来ます。
2つの入力信号をそれぞれ\(X_1(s)\)と\(X_2(s)\)、出力信号を\(Y(s)\)とします。
まず上の図のように、一方の入力信号\(X_1(s)\)が伝達要素\(G\)を通り、もう一方の入力信号\(X_2(s)\)はそのまま加え合わせ点によって足し合わされて出力信号\(Y(s)\)となる場合を考えます。
まず、入力信号\(X_1(s)\)が伝達要素\(G\)を通り出力される内部信号を\(C(s)\)とすると、
$$ C(s) = G X_1(s) $$
と求めることが出来ます。
そして、出力信号\(Y(s)\)は加え合わせ点によって、内部信号を\(C(s)\)と入力信号\(X_2(s)\)が足し合わされるので、
$$ Y(s) = C(s) + X_2(s) $$
と表すことが出来ます。
よって、出力信号(\(Y(s)\))と入力信号(\(X_1(s)\)と\(X_2(s)\))の関係は、伝達要素\(G\)を用いて、
$$ Y(s) = G X_1(s) + X_2(s) $$
と表すことが出来ます。
つぎに下の図のように、一方の入力信号\(X_1(s)\)がそのままで、もう一方の入力信号\(X_2(s)\)が伝達要素\(G\)の逆数を通った後、加え合わせ点によって足し合わされた信号が伝達要素\(G\)を通り出力信号\(Y(s)\)となる場合を考えます。
伝達要素\(G\)の逆数\(\frac{1}{G}\)から出力される内部信号\(C_1(s)\)は、入力信号\(X_2(s)\)と伝達要素\(\frac{1}{G}\)を用いて、
$$ C_1(s) = \frac{1}{G} X_2(s) $$
と表すことが出来ます。
次に加え合わせ点によって足し合わされた内部信号\(C_2(s)\)は、そのままにゅうう力される入力信号\(X_1(s)\)と内部信号\(C_1(s)\)を用いて、
$$ C_2(s) = X_1(s) + C_1(s) $$
となります。
さらに出力信号\(Y(s)\)は、内部信号\(C_2(s)\)と伝達要素\(G\)を用いて、
$$ Y(s) = G C_2(s) $$
と求めることが出来ます。
よって、出力信号(\(Y(s)\))は入力信号(\(X_1(s)\)と\(X_2(s)\))と伝達要素\(G\)を用いて、
$$ Y(s) = G \left(X_1(s) + C_1(s) \right) $$
$$ \Rightarrow Y(s) = G \left(X_1(s) + \left( \frac{1}{G} X_2(s) \right) \right) $$
$$ \Rightarrow Y(s) = G X_1(s) + X_2(s) $$
と算出することが出来ました。
これより、加え合わせ点の前にある伝達要素(上図)と引き出し点の後に移動させて、もう一方の入力信号に伝達要素の逆数を掛けた場合(下図)の出力信号は同じになることが分かりました。
まとめ
今回は、複雑なブロック線図を簡単化するために必要な伝達要素と加え合わせ点の関係についての知識を、数式を用いながら紹介しました。
今まで紹介してきたブロック線図の特性を用いることで、複雑なブロック線図を簡単化することが出来ます。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
