ボード線図の位相余裕とゲイン余裕から安定性を確認する方法

あるシステムを制御する際に、そのシステムが安定か不安定かを事前に確認することは、とても重要です。

システムが不安定の場合、入力によるシステムの応答が無限大に発散したりと、システムが制御不能になり暴走する可能性があります。

今回からの記事では、制御システムのボード線図からシステムの安定性を判別する方法を紹介します。

安定性の判別方法

システムが安定であるかを判別する条件として、システムの伝達関数G(s)

$$ G(s) = \frac{b_m s^m+b_{m-1} s^{m-1}+\cdots+b_1 s+b_0}{s^n+a_{n-1} s^{n-1}+\cdots+a_1 s+a_0} $$

から得られる特性方程式D(s)

$$ \begin{eqnarray} D(s) &=& 1 + G(s) \\ &=& b_m s^m+b_{m-1} s^{m-1}+\cdots+b_1 s+b_0 + s^n+a_{n-1} s^{n-1}+\cdots+a_1 s+a_0 \end{eqnarray} $$

について、解の実部がすべて負（マイナス）になる必要があります。

詳しくは、こちらの記事を参考にしてください。

伝達関数の極とインパルス応答 複素平面上での伝達関数の極の位置から、システムのインパルス応答の様子を見ることが出来ます。 今回は、ロボットなどの...

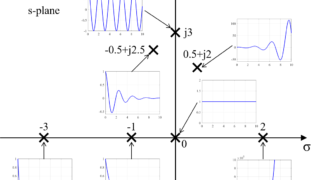
しかし、この特性方程式D(s)の次数が増えると、特性方程式を解く計算が難しく（ややこしく、面倒くさく）なります。

そのため、多くの場合はこの特性方程式を解かずに判別する方法を用いています。

安定性を判別する方法として、

• ラウス・フルビッツの安定判別法
• ボード線図による安定判別法
• ナイキスト線図による安定判別法

があります。

今回は、ボード線図を用いた安定判別法を紹介します。

ラウス・フルビッツの安定判別法については、こちらの記事を参考にしてください。

システムの安定性：ラウス・フルビッツの安定判別法 ロボットなどのシステムの安定性を判別することは、ロボットなどを制御する際にとても重要です。 前回の記事では、システ...

開ループ系のボード線図と安定余裕

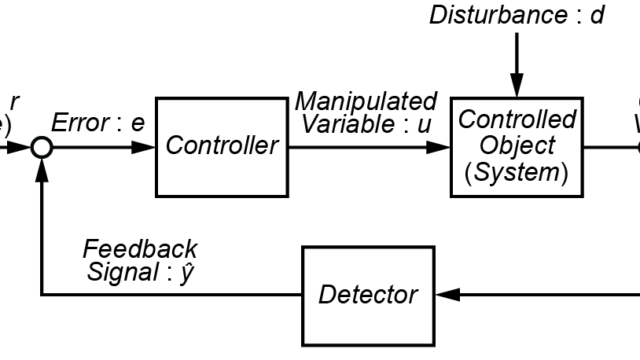
与えられた制御システムが安定か不安定かを確認する指標として、開ループ系の安定余裕を確認するという方法があります。

この安定余裕には、

• ゲイン余裕（Gain Margin）
• 位相余裕（Phase Margin）

の2つの項目があります。

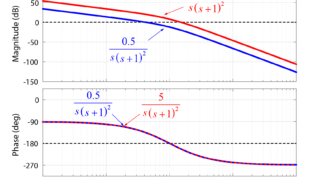
制御システムの開ループ系のボード線図が、下の図のように表された場合を考えます。

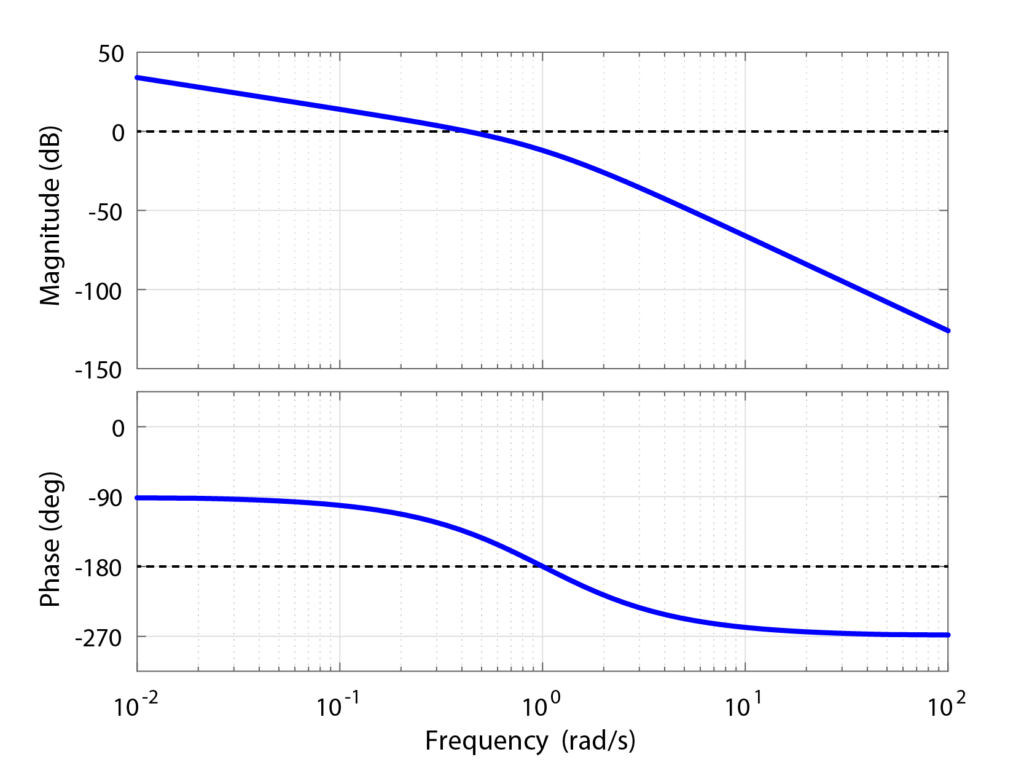
この開ループ系のボード線図から、システムのゲイン余裕と位相余裕を求めていきます。

ゲイン余裕

ゲイン余裕とは、位相が-180°の時のゲインと0dBとの差です。

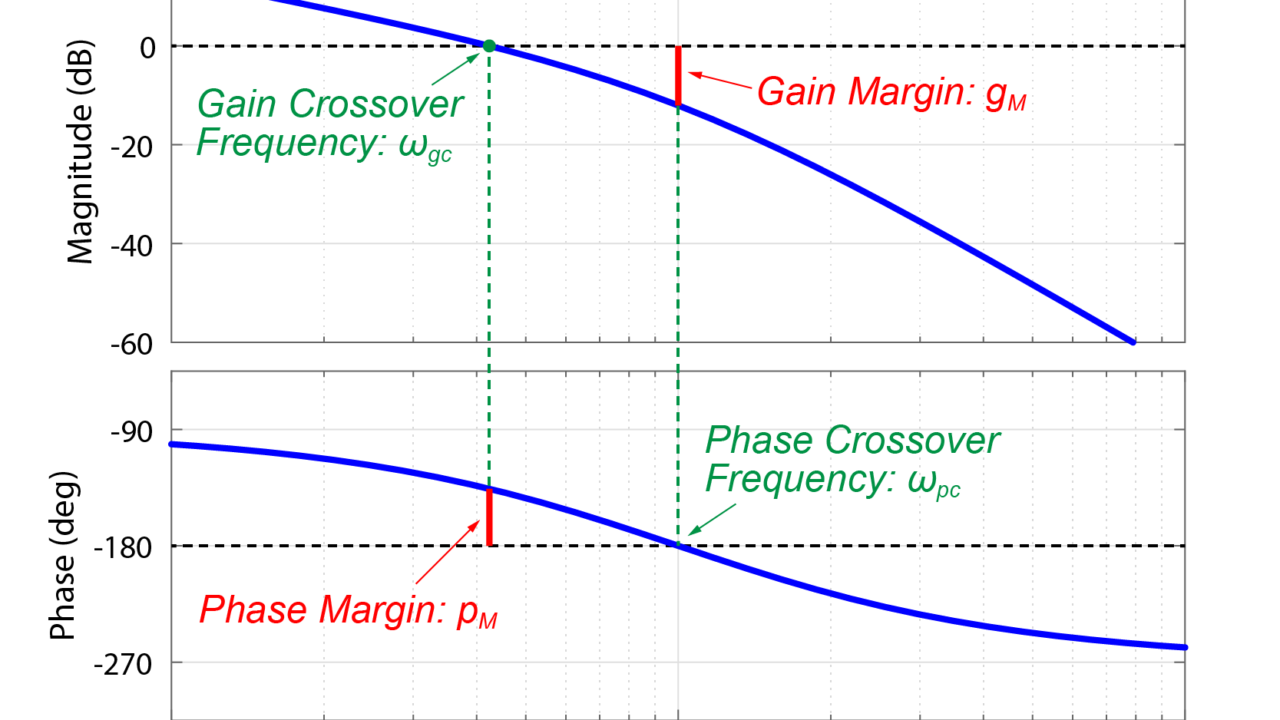
ボード線図を用いて表すと下図のようになります。

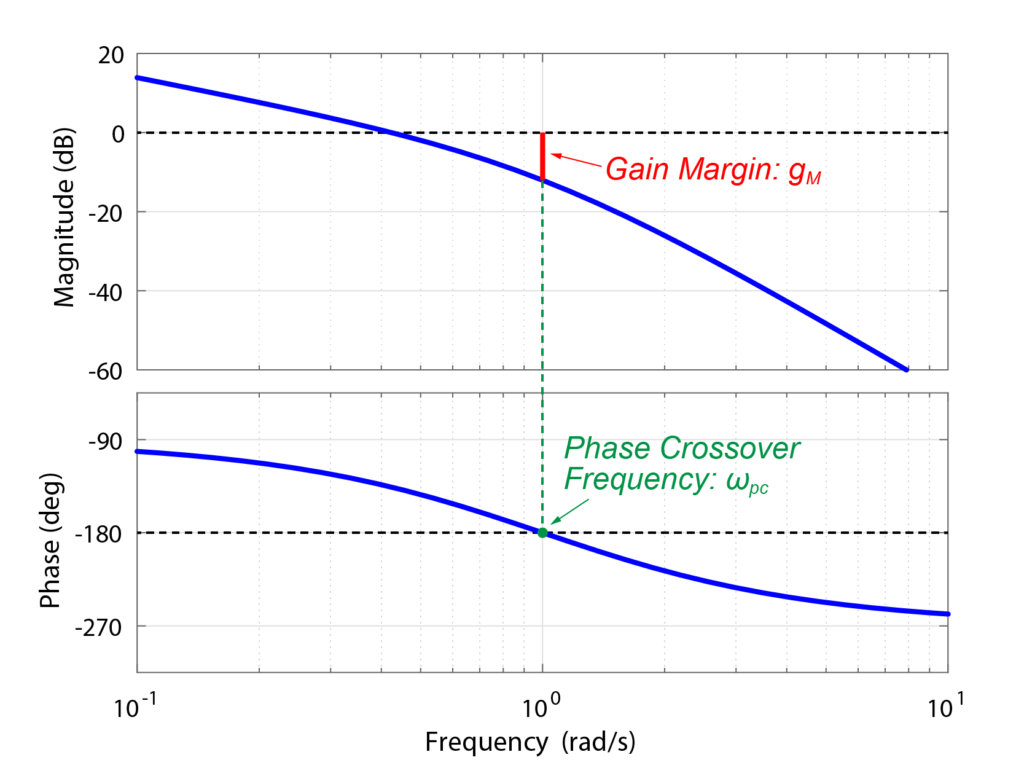
位相線図の値（下側グラフの青線）が-180°となるとき（緑点）の、ゲイン線図の値（上側グラフの青線）と0dBとの差（赤線）を、ゲイン余裕と言います。

この時の周波数（緑）を位相交差周波数（Phase Crossover Frequency）と呼びます。

位相余裕

位相余裕とは、ゲインが0dBの時の位相の値と-180°との差です。

ボード線図を用いて表すと下図のようになります。

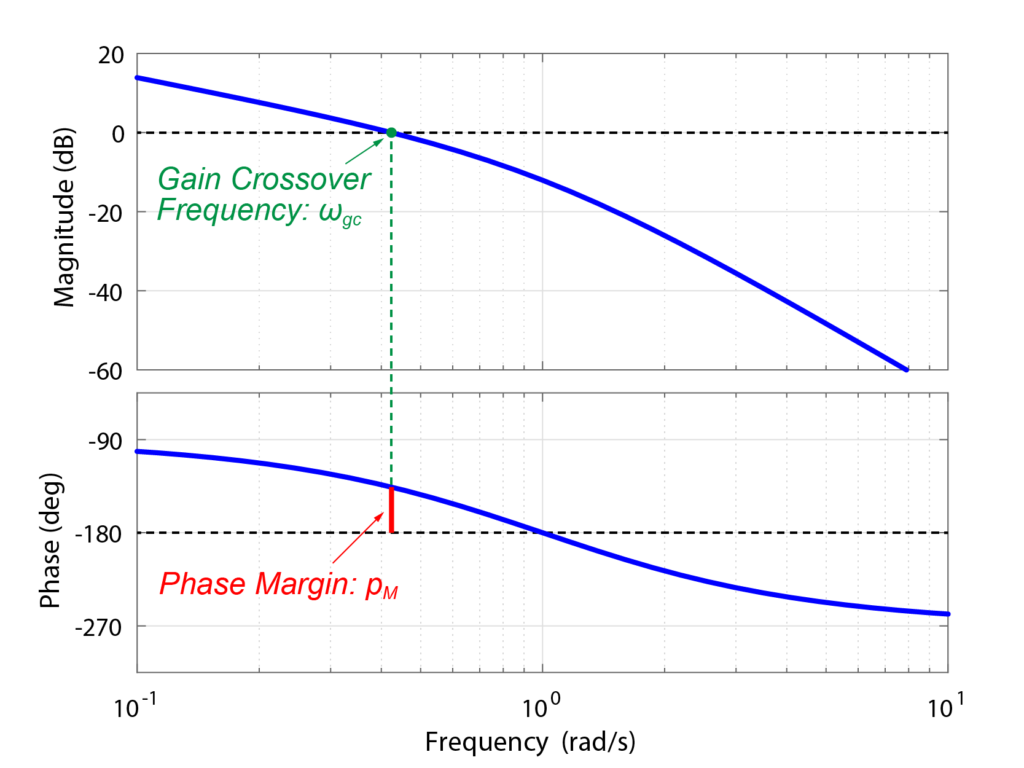
ゲイン線図の値（上側グラフの青線）が0dBとなるとき（緑点）の、位相線図の値（下側グラフの青線）と-180°との差（赤線）を、位相余裕と言います。

この時の周波数をゲイン交差周波数（Gain Crossover Frequency）といいます。

まとめ

今回の記事では、開ループ系のボード線図からゲイン余裕と位相余裕を求める方法を紹介しました。

次回の記事では、今回求めた安定余裕を用いてシステムの安定性を確認する方法を紹介したいと思います。

システムの安定性をボード線図の安定余裕から確認する方法 制御システムの安定性をボード線図を用いて判別する方法を紹介しています。 前回の記事では、開ループ系のボード線図から...