ボード線図を用いてシステムの周波数特性を表す：ゲインと位相の算出

ボード線図を用いることで、フィードバックシステムの周波数特性が理解しやすくなります。

前回の記事では、ボード線図について基本的な知識を紹介しました。

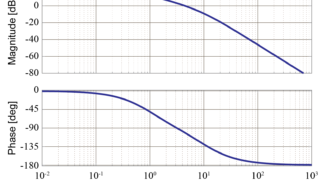
ボード線図を用いてシステムの周波数特性を表す：基本知識ボード線図を用いることでフィードバックシステムの周波数特性を求めることが出来ます。今回の記事では、ボード線図とそ...

今回は、実際に具体的な値を用いてボード線図を描くために必要となる計算方法を紹介します。

Contents

取り扱うシステム
出力信号を求める
ゲインと位相を算出する
- ゲインを求める
- 位相を求める
ボード線図を書く
まとめ

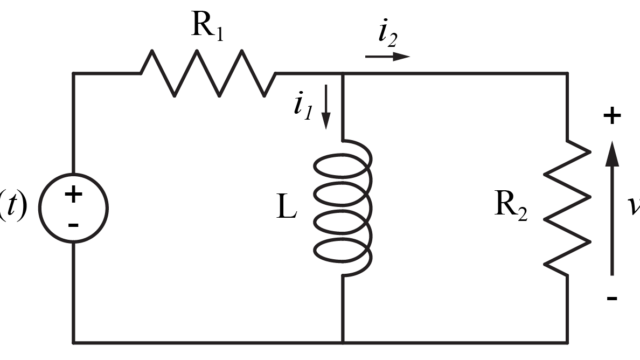
取り扱うシステム

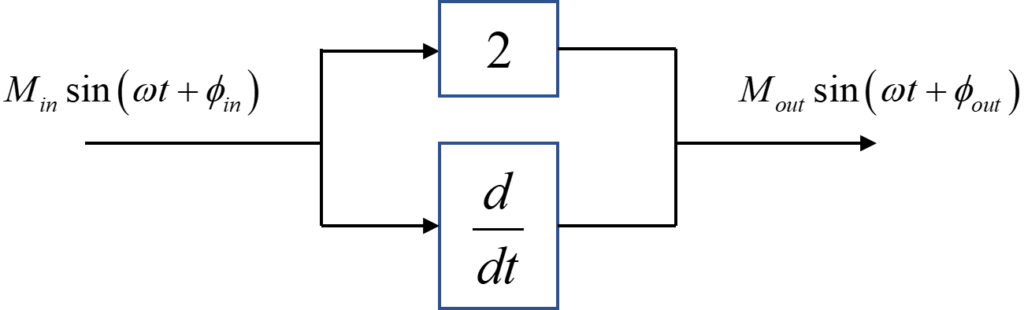
今回は上図のようなシステムについて、入力信号と出力信号の関係を求めることで、ボード線図を描いていきます。

今回の例では、入力信号$u(t)$を

$$ \begin{eqnarray} u(t) &=& M_{in} \sin (\omega t + \phi_{in}) \\ &=& \sin (2 t) \end{eqnarray} $$

とします。

ここで、入力信号$u(t)$内の各パラメータは

$$ \begin{eqnarray} \left\{ \begin{array}{l} M_{in} &=& 1 \\ \omega &=& 2 \\ \phi_{in} &=& 0 \end{array} \right. \end{eqnarray} $$

で表されます。

出力信号を求める

先程の入力信号$u(t)$を今回のシステムに入力した際の出力信号$y(t)$を算出していきます。

今回のシステムは、入力信号$u(t)$を2倍したものと微分したものを加え合わせて、出力信号$y(t)$としています。

よって、この入力信号$u(t)$をシステムに入力した際の出力信号$y(t)$は

$$ y(t) = 2 \sin (2 t) + 2 \cos (2 t) $$

で求められます。

この出力信号$y(t)$を

$$ y(t) = M_{out} \sin (\omega t + \phi_{out}) $$

の形に整理すると、

$$ \begin{eqnarray} y(t) &=& 2 \sin (2 t) + 2 \cos (2 t) \\ &=& \sqrt{2^2+2^2} \sin \left(2 t + \arctan \left(\frac{2}{2}\right) \right) \\ &=& 2\sqrt{2} \sin \left(2 t + \frac{\pi}{4} \right) \end{eqnarray} $$

と表すことが出来ます。

この式より、入力信号$y(t)$内の各パラメータは

$$ \begin{eqnarray} \left\{ \begin{array}{l} M_{in} &=& 2\sqrt{2} \\ \omega &=& 2 \\ \phi_{in} &=& \frac{\pi}{4} \end{array} \right. \end{eqnarray} $$

と求められることが分かりました。

ゲインと位相を算出する

算出した出力信号$y(t)$を基に、入力信号$u(t)$に対するゲインと位相の変化を求めていきます。

ゲインを求める

ボード線図を構成する2つのグラフの内の1つであるゲイン線図の縦軸は通常$[dB]$（デシベル）という単位を用いて表されます。

このゲイン\(G [dB]は入力信号と出力信号の振幅の比を用いて

$$ G = 20 \log \left( \frac{M_{out}}{M_{in}} \right) $$

と算出されます。

この関係式を用いて、実際に今回の例のゲインを求めると

$$ \begin{eqnarray}G &=& 20 \log \left( \frac{2\sqrt{2}}{1} \right) \\ &=& 9.031 [dB] \end{eqnarray} $$

と求めることが出来ました。

位相を求める

ボード線図を構成する2つのグラフの内のもう1つ、位相線図の縦軸について単位は通常$[^\circ]$（度）を用いて表されます。

この位相は、入力信号と出力信号を用いて

$$ \phi = \phi_{out} – \phi_{in} $$

のように2つの信号の差から求めることが出来ます。

この関係式を用いて、実際に今回の例の位相を求めると

$$ \begin{eqnarray} \phi &=& 45^{\circ} – 0 \\ &=& 45^{\circ} \end{eqnarray} $$

と求めることが出来ました。

これより、信号の周波数$\omega$が

$$ \omega = 2 $$

の場合のボード線図のゲインと位相の値はそれぞれ

$$ \begin{eqnarray} \left\{ \begin{array}{l} G &=& 9.031 [dB] \\ \phi &=& 45 [^{\circ}] \end{array} \right. \end{eqnarray} $$

となる事が分かりました。

ボード線図を書く

この様な計算を角周波数に対して行うことでボード線図を書くことが出来ます。

入力信号$u(t)$の周波数$\omega$が

$$ \omega = \frac{1}{2} = 0.5 $$

の場合、出力信号$y(t)$は

$$ \begin{eqnarray} y(t) &=& 2 \sin (0.5 t) + 0.5 \cos (0.5 t) \\ &=& \sqrt{2^2+{0.5}^2} \sin \left(0.5 t + \arctan \left(\frac{0.5}{2}\right) \right) \\ &=& 2.062 \sin \left(2 t + 0.245 \right) \end{eqnarray} $$

と求められます。

よって、ゲインと位相の値はそれぞれ

$$ \begin{eqnarray} \left\{ \begin{array}{l} G &=& 6.284 [dB] \\ \phi &=& 14.04 [^{\circ}] \end{array} \right. \end{eqnarray} $$

と算出されます。

しかし、このような計算を全ての周波数に対して行う事は現実的ではありません。

そのため、伝達関数からボード線図の概略を書く方法があります。