ボード線図を用いてシステムの周波数特性を表す：基本知識

ボード線図を用いることでフィードバックシステムの周波数特性を求めることが出来ます。

今回の記事では、ボード線図とその基本知識について紹介していきたいと思います。

ボード線図とは

ボード線図（Bode Plot）とは、入力信号を線形時不変システムに入力した際の出力信号の周波数特性を表した図の事です。

振幅の増幅を示すゲイン線図と、位相の変化を示す位相線図の2つで成り立っています。

ボード線図の横軸は周波数となっているため、ボード線図を用いることで、対象の周波数をもつ信号がシステムに入力された場合の出力信号の様子を理解することが出来ます。

このボード線図を構成する2つのグラフ（ゲイン線図と位相線図）を書くために必要となる基本知識を紹介していきます。

ボード線図の基本知識

システムが安定した状態では、線形時不変システムに入力された正弦信号（sin波やcos波）は、同じ周波数を保ったまま出力されます。

入力信号と出力信号の周波数は同じですが、入力信号と出力信号の振幅と位相には変化が生じます。

この振幅と位相の変化は、入力信号の周波数の関数として表すことが出来ます。

入力信号\(u(t)\)が

$$ u(t) = M_i \sin \left( \omega t + {\phi}_i \right) $$

で表されるとします。

この時の入力信号の周波数は\(\omega\)で、振幅は\(M_i\)、位相は\({\phi}_i\)となります。

この正弦信号\(u(t)\)を線形時不変システムに入力した際の出力信号\(y(t)\)は、

$$ y(t) = M_o \sin \left( \omega t + {\phi}_o \right) $$

で表すことが出来ます。

入力信号\(u(t)\)の場合と同様に、この時の出力信号\(y(t)\)の周波数は\(\omega\)となり、振幅は\(M_o\)、位相は\({\phi}_o\)と変化します。

この2つの信号（入力信号\(u(t)\)と出力信号\(y(t)\)）を表す式から、入力信号\(u(t)\)と出力信号\(y(t)\)は異なる振幅と位相を持つ同じ周波数の信号であると分かります。

この時の振幅の変化\(M(\omega)\)は

$$ M(\omega) = \frac{M_o(\omega)}{M_i(\omega)} $$

で求めることが出来ます。

また、位相の変化\(\phi(\omega)\)は

$$ \phi(\omega) = {\phi}_o (\omega) – {\phi}_i (\omega) $$

と求めることが出来ます。

これら振幅\(M(\omega)\)と位相の変化\(\phi(\omega)\)の変化を角周波数で求めてグラフ化したものがボード線図です。

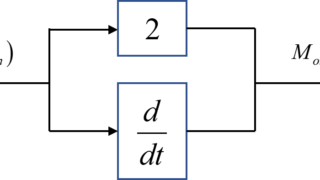
ブロック線図で表す

先ほど求めた線形時不変システムに対する入力信号と出力信号の関係をブロック線図で表したいと思います。

前に正弦信号の形で表した入力信号\(u(\omega)\)は

$$ u(\omega) = M_i (\omega) \angle {\phi}_i (\omega) $$

の形で表すことが出来ます。

同様に、出力信号\(y(\omega)\)も

$$ y(\omega) = M_o (\omega) \angle {\phi}_o (\omega) $$

で表すことが出来ます。

制御システムについても同様の形で表すと

$$M (\omega) \angle {\phi} (\omega) $$

と表すことが出来ます。

この時の振幅\(M(\omega)\)と位相\(\phi(\omega)\)は、

$$ \begin{eqnarray} \left\{ \begin{array}{l} M(\omega) &=& \frac{M_o(\omega)}{M_i(\omega)} \\ \phi(\omega) &=& {\phi}_o (\omega) – {\phi}_i (\omega) \end{array} \right. \end{eqnarray} $$

のように、先に求めた方法で求めることが出来ます。

まとめ

今回は、ボード線図の基本的な知識について紹介しました。

ボード線図を用いることで、システムの周波数特性を得ることが出来ます。

次回は、具体的な値を用いて実際にボード線図を求めていきたいと思います。

ボード線図を用いてシステムの周波数特性を表す：ゲインと位相の算出 ボード線図を用いることで、フィードバックシステムの周波数特性が理解しやすくなります。 前回の記事では、ボード線図に...