台車型倒立振子の運動方程式をラグランジュ方程式で求める（その２）

前回の記事の続きとして、台車型倒立振子の運動方程式をラグランジュ方程式を用いて求めていく方法を紹介します。

台車型倒立振子の運動方程式をラグランジュ方程式で求める 倒立振子が台車の上に乗っているシステムを台車型倒立振子と言います。 この台車型倒立振子を制御する際には運動方程式を...

前回のまで記事では、台車型倒立振子の運動方程式を紹介して、ラグランジュ方程式を用いるために運動エネルギーと位置エネルギーを算出しました。

今回の記事では、前回求めた運動エネルギーと位置エネルギーからラグランジュ方程式を用いた運動方程式の求め方を紹介します。

台車型倒立振子と運動方程式

前回のおさらいです。

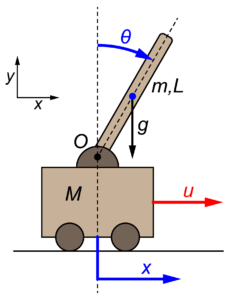
台車型倒立振子とは、下の図のように倒立振子が台車の上に設置されたモデルです。

このときの台車型倒立振子の運動方程式は

$$ \begin{eqnarray} \left\{ \begin{array}{l} \left( M + m \right) \ddot{x} + \frac{1}{2} m L \cos (\theta) \ddot{\theta} -\frac{1}{2} m L \sin (\theta) \dot{\theta}^2 = u \\ \frac{1}{2} m L \cos (\theta) \ddot{x} – \frac{1}{2} m L \sin (\theta) \dot{x} \dot{\theta} + \frac{1}{3} m L^2 \ddot{\theta} – \frac{1}{2} m g L \sin (\theta) = 0 \end{array} \right. \end{eqnarray} $$

と表すことが出来ます。

この運動方程式を、前回求めた運動エネルギーと位置エネルギーからラグランジュ方程式を用いて実際に算出していきます。

ラグランジュ方程式と運動方程式

システム内に外力Fが存在する場合のラグランジュ方程式の一般式は

$$ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}} KE \right) + \frac{\partial}{\partial x} PE = F $$

と表すことが出来ます。

この式に含まれる運動エネルギーKEと位置エネルギーPEについて、前回求めた台車型倒立振子の運動エネルギーKEと位置エネルギーPE

$$ \begin{eqnarray} \left\{ \begin{array}{l} KE &=& \frac{1}{2} M \dot{x}^2 + \frac{1}{2} m \left[ \dot{x}^2 + L \cos (\theta) \dot{x} \dot{\theta} + \frac{L^2}{4} \dot{\theta}^2 \right] + \frac{1}{2} \left[ \frac{1}{12} m L^2 \right] \dot{\theta}^2 \\ PE &=& \frac{m g L}{2} \cos (\theta) \end{array} \right. \end{eqnarray} $$

を代入して、台車型倒立振子の運動方程式を求めていきます。

運動エネルギーと位置エネルギーの詳しい求め方は、こちらの記事を参考にしてください。

台車型倒立振子の運動方程式をラグランジュ方程式で求める 倒立振子が台車の上に乗っているシステムを台車型倒立振子と言います。 この台車型倒立振子を制御する際には運動方程式を...

今回取り扱っている台車型倒立振子のモデルでは、変数が台車の変位xと振り子の角度θが含まれています。

よって、ラグランジュ方程式の一般式に含まれる変数xは

$$ x = \{ x , \theta \} $$

となります。

また外力Fについては、台車にかかる力uが存在し、棒振り子には力はかかっていないため

$$ F = \{ u , 0 \} $$

と表すことが出来ます。

よって、今回の台車型倒立振子のラグランジュ方程式は

$$ \begin{eqnarray} \left\{ \begin{array}{l} \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}} KE \right) + \frac{\partial}{\partial x} PE = u \\ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{\theta}} KE \right) + \frac{\partial}{\partial \theta} PE = 0 \end{array} \right. \end{eqnarray} $$

の２式となります。

この2つのラグランジュ方程式について、それぞれの変数（xとθ）について解くことで、台車型倒立振子の運動方程式を求めることが出来ます。

変数xについて解く

はじめに、台車の変位xについてのラグランジュ方程式

$$ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}} KE \right) + \frac{\partial}{\partial x} PE = u $$

を解くことで、運動方程式を求めていきたいと思います。

まず運動エネルギー（KE）について、ラグランジュ方程式に含まれる運動エネルギー（KE）を変位の時間微分（\(\dot{x}\)）で偏微分した結果を求めます。

$$ \begin{eqnarray} \frac{\partial}{\partial \dot{x}} KE &=& \frac{\partial}{\partial \dot{x}} \left( \frac{1}{2} M \dot{x}^2 + \frac{1}{2} m \left[ \dot{x}^2 + L \cos (\theta) \dot{x} \dot{\theta} + \frac{L^2}{4} \dot{\theta}^2 \right] + \frac{1}{2} \left[ \frac{1}{12} m L^2 \right] \dot{\theta}^2 \right) \\ &=& M \dot{x} + m \dot{x} + \frac{1}{2} m L \cos (\theta) \dot{\theta} \end{eqnarray} $$

そして、求めた結果を時間微分します。

$$ \begin{eqnarray} \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}} KE \right) &=& \frac{d}{dt} \left( M \dot{x} + m \dot{x} + \frac{1}{2} m L \cos (\theta) \dot{\theta} \right) \\ &=& M \ddot{x} + m \ddot{x} + \frac{1}{2} m L \cos (\theta) \ddot{\theta} -\frac{1}{2} m L \sin (\theta) \dot{\theta}^2 \end{eqnarray} $$

さらに、位置エネルギー（PE）を変位（x）で微分します。

$$ \begin{eqnarray} \frac{\partial}{\partial x} PE &=& \frac{\partial}{\partial x} \left( \frac{m g L}{2} \cos (\theta) \right) \\ &=& 0 \end{eqnarray} $$

今回は、位置エネルギーPEに台車の変位xが含めれていないため、結果は0になります。

最後に、求めた結果を足し合わせて変位xについての運動方程式は

$$ M \ddot{x} + m \ddot{x} + \frac{1}{2} m L \cos (\theta) \ddot{\theta} -\frac{1}{2} m L \sin (\theta) \dot{\theta}^2 = u $$

と求めることが出来ました。

変数θについて解く

つぎに、棒振り子の角度θについてのラグランジュ方程式

$$ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{\theta}} KE \right) + \frac{\partial}{\partial \theta} PE = 0 $$

を解いて、運動方程式を求めていきたいと思います。

基本的に求め方は台車の変位xの場合と同じです。

まず運動エネルギー（KE）について、ラグランジュ方程式に含まれる運動エネルギー（KE）を棒振り子の角度（θ）の時間微分（\(\dot{\theta}\)）で偏微分した結果を求めます。

$$ \begin{eqnarray} \frac{\partial}{\partial \dot{\theta}} KE &=& \frac{\partial}{\partial \dot{\theta}} \left( \frac{1}{2} M \dot{x}^2 + \frac{1}{2} m \left[ \dot{x}^2 + L \cos (\theta) \dot{x} \dot{\theta} + \frac{L^2}{4} \dot{\theta}^2 \right] + \frac{1}{2} \left[ \frac{1}{12} m L^2 \right] \dot{\theta}^2 \right) \\ &=& \frac{1}{2} m L \cos (\theta) \dot{x} + m \frac{L^2}{4} \dot{\theta} + \frac{1}{12} m L^2 \dot{\theta} \end{eqnarray} $$

そして、求めた結果を時間微分します。

$$ \begin{eqnarray} \frac{d}{dt} \left( \frac{\partial}{\partial \dot{\theta}} KE \right) &=&  \frac{d}{dt} \left( \frac{1}{2} m L \cos (\theta) \dot{x} + m \frac{L^2}{4} \dot{\theta} + \frac{1}{12} m L^2 \dot{\theta} \right) \\ &=& \frac{1}{2} m L \cos (\theta) \ddot{x} – \frac{1}{2} m L \sin (\theta) \dot{x} \dot{\theta} + m \frac{L^2}{4} \ddot{\theta} + \frac{1}{12} m L^2 \ddot{\theta} \end{eqnarray} $$

さらに、位置エネルギー（PE）を角度（θ）で微分します。

$$ \begin{eqnarray} \frac{\partial}{\partial \theta} PE &=& \frac{\partial}{\partial \theta} \left( \frac{m g L}{2} \cos (\theta) \right) \\ &=& – \frac{m g L}{2} \sin (\theta) \end{eqnarray} $$

よって、棒振り子の角度θについての運動方程式は、求めた結果を足し合わせて

$$ \frac{1}{2} m L \cos (\theta) \ddot{x} – \frac{1}{2} m L \sin (\theta) \dot{x} \dot{\theta} + m \frac{L^2}{4} \ddot{\theta} + \frac{1}{12} m L^2 \ddot{\theta} – \frac{m g L}{2} \sin (\theta) = 0 $$

と求めることが出来ます。

全体の運動方程式

さきに求めたそれぞれの変数（変位xと角度θ）についての運動方程式より、今回の台車型倒立振子の運動方程式は

$$ \begin{eqnarray} \left\{ \begin{array}{l} \left( M + m \right) \ddot{x} + \frac{1}{2} m L \cos (\theta) \ddot{\theta} -\frac{1}{2} m L \sin (\theta) \dot{\theta}^2 = u \\ \frac{1}{2} m L \cos (\theta) \ddot{x} – \frac{1}{2} m L \sin (\theta) \dot{x} \dot{\theta} + \frac{1}{3} m L^2 \ddot{\theta} – \frac{1}{2} m g L \sin (\theta) = 0 \end{array} \right. \end{eqnarray} $$

と求めることが出来ました。

（おまけ）運動方程式を線形化する

今回の記事で求めた台車型倒立振子の運動方程式には、三角関数（sin(θ)やcos(θ)）が含まれています。

そのため、運動方程式は非線形な関数になっています。

この非線形なシステムの取り扱いを簡単にするために、運動方程式を線形化する方法を紹介します。

まず、棒振り子の角度θが十分に小さいとします。

この条件の場合、三角関数（sin(θ)やcos(θ)）について

$$ \begin{eqnarray} \left\{ \begin{array}{l} \cos (\theta) \approx 1 \\ \sin (\theta) \approx \theta \end{array} \right. \end{eqnarray} $$

と近似することが出来ます。

さらに、角度θが十分に小さいとすると、角速度\(\dot{\theta}\)を含む項について

$$ \begin{eqnarray} \left\{ \begin{array}{l} \dot{\theta}^2 \approx 0 \\ \theta \dot{\theta} \approx 0 \end{array} \right. \end{eqnarray} $$

のように扱うことが出来ます。

よって、非線形システムであった台車型倒立振子の運動方程式は

$$ \begin{eqnarray} \left\{ \begin{array}{l} \left( M + m \right) \ddot{x} + \frac{1}{2} m L \ddot{\theta}  = u \\ \frac{1}{2} m L \ddot{x} + \frac{1}{3} m L^2 \ddot{\theta} – \frac{1}{2} m g L \theta = 0 \end{array} \right. \end{eqnarray} $$

のように線形のシステムとして表すことが出来ました。

まとめ

今回の記事では、台車型倒立振子の運動エネルギーと位置エネルギーをラグランジュ方程式に代入することで、運動方程式を求める方法を紹介しました。

また、非線形な式で表された運動方程式を線形な運動方程式に変換する方法も紹介しました。

前回と今回で求めた運動方程式を用いることで、台車型倒立振子を制御することが可能になります。

合わせて読みたい

算出した運動方程式から状態方程式を求める方法を紹介します。

台車型倒立振子を制御するために状態方程式を求める 台車の上に倒立振子が設置されているシステムを台車型倒立振子と言います。 この台車型倒立振子を制御するために、システ...