複雑なブロック線図を簡単化して、シンプルなブロック線図に簡略化することで、システムを取り扱いやすく、制御しやすくすることが出来ます。
このブロック線図の簡略化の手法としては
- 内部信号を定義して算出する方法
- ブロック線図の特性を利用する方法
があります。
この2つの手法のうち、2つ目のブロック線図の特性を利用する方法は、実際にどのような流れで考えれば良いかが分からず難しいと感じる方が多くいます。
私も最初はそう感じていました。
今回の記事では、ブロック線図の特性を利用して簡略化する方法について、私が使っている考え方のステップを紹介します。
ブロック線図の特性を利用する利点
まず初めに、ブロック線図の特性を利用する手法の利点を紹介したいと思います。
内部信号を利用する手法では、ブロック線図が複雑化するにつれて連立方程式の未知数が増えるため、計算量が上がり解くことが大変になるという問題があります。
そこで、ブロック線図の特性を利用することで、多くの計算が必要ではなくなり、パズルを解くようにブロック線図の簡略化を行うことが出来ます。
しかし、このパズルのように解くという部分にヒラメキが必要となるため、どのように考えれば良いかが難しくなります。
そこで、今回紹介する考え方の流れを用いることで、複雑なブロック線図を着実にシンプルなブロック線図に簡略化することが出来ます。
考え方のステップ
では、複雑なブロック線図が与えられた場合に、ブロック線図の特性を利用して簡単化するために考え方のフローを紹介します。
ステップ1：直列回路と並列回路をまとめる
ステップ2：フィードバック回路をまとめる
ステップ3：引き出し点の分解と移動
ステップ4：加え合わせ点の分解と移動
上のフローのように、私が使っているブロック線図の簡略化のための考え方では、大きく4つのステップがあります。
ステップ1：直列回路と並列回路をまとめる
まず最初のステップとして、ブロック線図に含まれる直列回路と並列回路（フィードフォワード）をまとめていきます。
直列回路と並列回路を含むブロック線図の簡略化についての詳細は、こちらの記事を参考にしてください。
直列回路と並列回路をどんどんまとめていくことで、ブロック線図内に含まれる伝達要素の数を減らすことができます。
ここで大事なポイントは、一つの直列回路または並列回路を簡略化したらその周りの伝達要素との関係を確認し、新しく直列回路や並列回路が出来ていないかどうかを確認することです。
このステップ1でどれくらい小さな塊を作れるかで、次からのステップの関係を見つけやすくなります。
ステップ2：フィードバック回路をまとめる
次のステップは、ブロック線図内に含まれるフィードバック回路の部分をまとめます。
フィードバック部分を1つの伝達関数にまとめる方法についての詳細は、こちらの記事を参考にしてください。
ここでのポイントは、フィードバック回路の中に分岐点や組み合わせ点を含まず、2つの伝達要素（フィードバック伝達要素が無い場合は1つの伝達要素）のみで構成されている、シンプルなフィードバック部分を見つけることです。
ブロック線図内にフィードバックしている信号があっても、複雑に絡み合ってシンプルなフィードバック部分が見つけづらくなっている場合があります。
複雑なブロック線図の中から、単純なフィードバック部分を見つけ出し、出来るだけ簡略化していきます。
そして、フィードバック部分を1つの伝達要素でまとめたら、ステップ1に戻って周りの伝達要素との関係を確認します。
ステップ3：引き出し点の分解と移動
直列回路と並列回路（フォードフォワード回路）、そしてフィードバック回路をまとめてもブロック線図の簡略化が終わらない場合は、引き出し点（分岐点）の分解や移動について考えます。
引き出し点の分解や移動をさせる方法の詳細は、こちらの記事を参考にしてください。
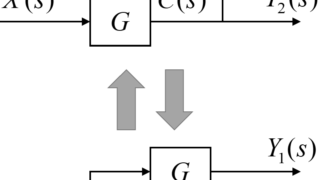
ここでのポイントは、引き出し点を移動させることで新しくフォードフォワード回路やフィードバック回路が出来るように考えることです。
かたまった引き出し点を分解したり、引き出し点同士の位置を移動したりすることで、組み合わさっているフィードバック回路をシンプルすることが出来ます。
例えば、フィードバック回路の中に他のフィードバック回路がある形にするなどします。
そして、新しく組み合わせ点を変更したらステップ1に戻って直列回路を並列回路をまとめて、ステップ2でフィードバック回路をまとめます。
注意してほしいことは、引き出し点と加え合わせ点の位置の入れ替えは出来ないということです。
引き出し点は引き出し点同士、そしてステップ4で扱う加え合わせ点は加え合わせ点同士で必ず処理を行います。
ステップ4：加え合わせ点の分解と移動
これでもブロック線図の簡単化は終わらない場合は、最後に加え合わせ点の分解や移動について考えます。
加え合わせ点の分解や移動をする方法の詳細は、こちらの記事を参考にしてください。
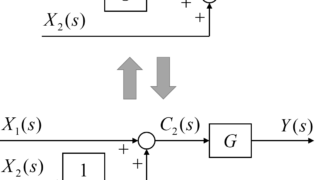
ここでのポイントも引き出し点と同様に、新しくフォードフォワード回路やフィードバック回路が出来るように加え合わせ点の分解や移動を考えることです。
また、ステップ3の引き出し点についてでも言及しましたが、加え合わせ点と引き出し点の位置を移動させることはできません。
加え合わせ点同士の位置を入れ替えたりすることで、ブロック線図の簡略化を進めていきます。
そして他のステップと同様に、加え合わせ点の分解や移動を行った場合は、もう一度ステップ1に戻ります。
このように、ステップ1から4まで順に考えていき、各ステップで処理を行った場合はもう一度ステップ1に戻り、伝達関数を簡単化していきます。
まとめ
今回の記事では、ブロック線図の特性を利用して簡略化する方法について、私が普段使っている考え方のステップを紹介しました。
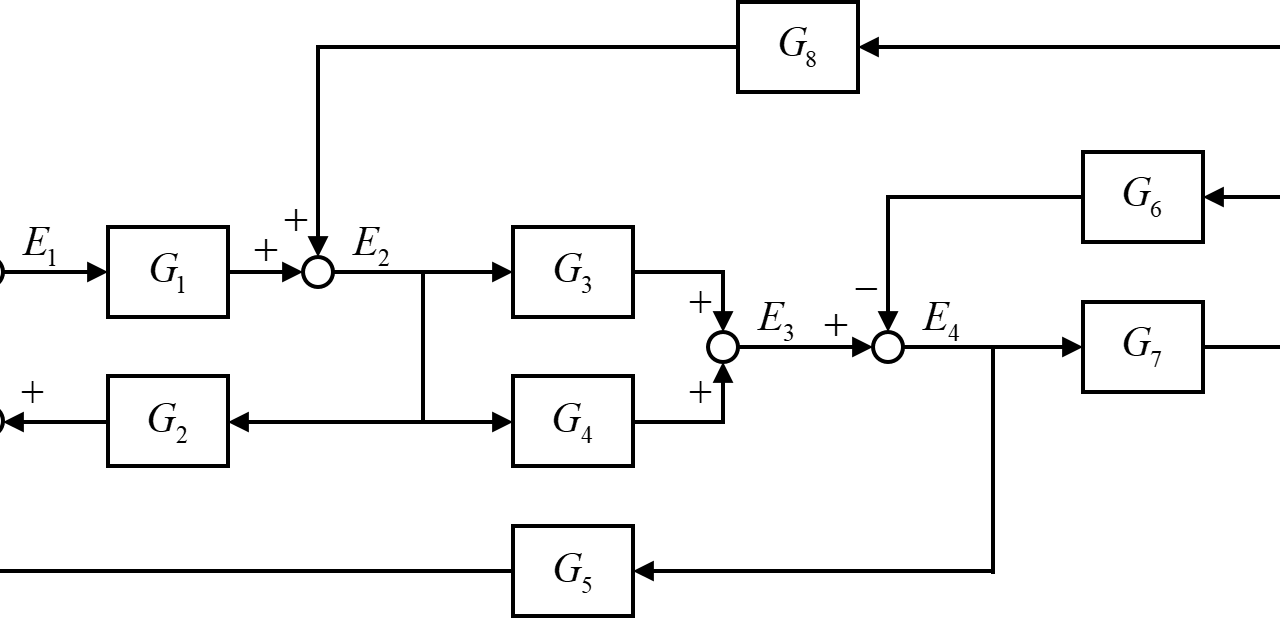
紹介したような考え方をすることで、パズルの様でどこから手を付ければ良いか分からなかったブロック線図の簡略化を、1つずつ順に進めることが出来ます。
ELEGOO Arduinoスターターキット
UNO R3スマートロボットカー
Raspberry Pi 3 Model b+
