このシリーズでは、ロボットや自動運転車を制御する際に重要な、ロボットや車の正確な位置を得る方法として、カルマンフィルタを用いたロボットの位置推定の方法を紹介しています。
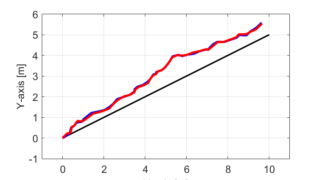
以前の記事では、移動ロボットの自己位置推定を行うために、カルマンフィルタを用いたアルゴリズムをMATALABで実装し、シミュレーションで動作の確認を行いました。
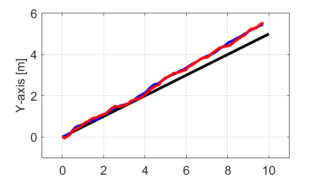
今回の記事では、シミュレーションの際に使用したプログラム(MATLAB)について説明したいと思います。
取り扱う自己位置推定問題
今回のシミュレーションでは、ロボットの状態空間モデルが
$$ \begin{eqnarray} \left\{ \begin{array}{l} \begin{bmatrix} x_t \\ y_t \end{bmatrix} &=& \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x_{t-1} \\ y_{t-1} \end{bmatrix} + \begin{bmatrix} 0.2 \\ 0.1 \end{bmatrix} + \begin{bmatrix} w_1 \\ w_2 \end{bmatrix} \\ \begin{bmatrix} z_{x,t} \\ z_{y,t} \end{bmatrix} &=& \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x_{t-1} \\ y_{t-1} \end{bmatrix} + \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} \end{array} \right. \end{eqnarray} $$
で表される線形システムについて、自己位置推定を行います。
詳しくは、こちらの記事を参考にしてください。

使用したプログラム
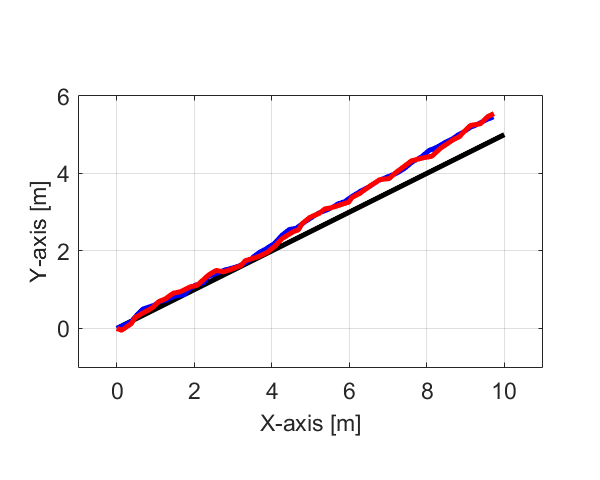
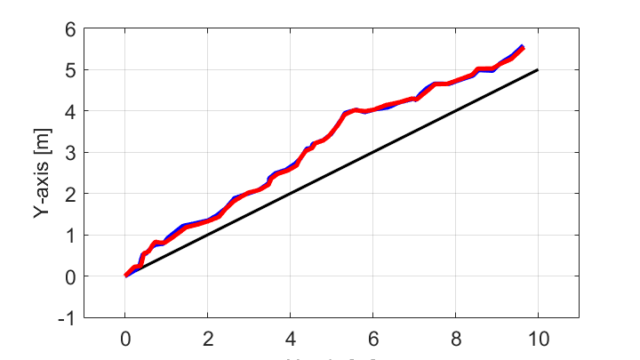
今回の記事で取り扱っている移動ロボットの自己位置推定の問題について、以下のMATALABのプログラム(コード)を用いてシミュレーションを行いました。
clear; close all; F = eye(2); % State Matrix H = eye(2); % Output Matrix u = [0.2;0.1]; % Input Signal Vector w = [0.04;0.04]; % Input Gaussian noise v = [0.09;0.09]; % Output Gaussian noise Q = diag(w); % Covariance Matrix R = diag(v); % Covariance Matrix xDes = [0;0]; % Desired State xAct = [0;0]; % Actual State xEst = [0;0]; % Estimated State P = eye(2); % Initialize Covariance Matrix Out.xDes = xDes; % Desired Trajectory Out.xAct = xAct; % Actual Trajectory Out.xEst = xEst; % Estimated Trajectory for t = 1:50 xDes = StateEquation(xDes,u,w*0); % Update Desired State xAct = StateEquation(xAct,u,w); % Update Actual State z = OutputEquation(xAct,v); % Get Observation Value xEst = F*xEst + u; % Predicted State Estimate P = F*P*F' + Q; % Predicted Error Covariance y = z - H*xEst; % Innovation or Measurement Pre-fit Residual S = R + H*P*H'; % Innovation or Pre-fit Residual Covariance K = P*H'/S; % Optimal Kalman Gain xEst = xEst + K*y; % Updated State Estimate P = (eye(2) - K*H)*P; % Updated Estimate Covariance Out.xDes = [Out.xDes,xDes]; Out.xAct = [Out.xAct,xAct]; Out.xEst = [Out.xEst,xEst]; end time = 0:1:length(Out.xAct)-1; figure; plot(Out.xDes(1,:),Out.xDes(2,:),'k',Out.xAct(1,:),Out.xAct(2,:),'b',Out.xEst(1,:),Out.xEst(2,:),'r','LineWidth',2); grid on; axis equal; axis([-1 11 -1 6]); xlabel('X-axis [m]'); ylabel('Y-axis [m]') return function x = StateEquation(x,u,w) x = x + u + normrnd(0,w); end function z = OutputEquation(x,v) z = x + normrnd(0,v); end
プログラム内で使用している理論や数式についての詳細は、こちらの記事を参考にしてください。

初期条件
シミュレーションに必要となる初期条件を以下のように設定します。
clear; close all; F = eye(2); % State Matrix H = eye(2); % Output Matrix u = [0.2;0.1]; % Input Signal Vector w = [0.04;0.04]; % Input Gaussian noise v = [0.09;0.09]; % Output Gaussian noise Q = diag(w); % Covariance Matrix R = diag(v); % Covariance Matrix xDes = [0;0]; % Desired State xAct = [0;0]; % Actual State xEst = [0;0]; % Estimated State P = eye(2); % Initialize Covariance Matrix Out.xDes = xDes; % Desired Trajectory Out.xAct = xAct; % Actual Trajectory Out.xEst = xEst; % Estimated Trajectory
初期条件を設定した後、for文を使って以下の項目を繰り返します。
ロボットの状態、センサ出力の算出
まず繰り返し部分の初めに、時刻tでのロボットの状態xとセンサによる観測値zを算出します。
xDes = StateEquation(xDes,u,w*0); % Update Desired State xAct = StateEquation(xAct,u,w); % Update Actual State z = OutputEquation(xAct,v); % Get Observation Value
今回は、プログラムの便利性を上げるために、それぞれロボットの状態とセンサの観測値を算出する関数(StateEquationとOutputEquation)を定義しました。
function x = StateEquation(x,u,w) x = x + u + normrnd(0,w); end function z = OutputEquation(x,v) z = x + normrnd(0,v); end
目標の状態xDesは雑音wを含めず算出するため、雑音wを0として状態xDesを算出します。
実際の状態xActの算出には雑音wによる影響を考慮するため、雑音wを含めて状態xActを算出します。
そして、実際の状態xActを用いてセンサによる観測値zを算出します。
予想ステップ
次に、1つ前の時刻t-1で推定したロボットの状態xEstと入力信号utから、時刻tでのロボットの状態xEstを推定します。
xEst = F*xEst + u; % Predicted State Estimate P = F*P*F' + Q; % Predicted Error Covariance
更新ステップ
そして、実際の観測値zと予測ステップで推定した状態xEstで得られるはずの観測値との差を求めることでカルマンゲインKを求め、ロボットの推定状態xEstを更新します。
y = z - H*xEst; % Innovation or Measurement Pre-fit Residual S = R + H*P*H'; % Innovation or Pre-fit Residual Covariance K = P*H'/S; % Optimal Kalman Gain xEst = xEst + K*y; % Updated State Estimate P = (eye(2) - K*H)*P; % Updated Estimate Covariance
結果保存~繰り返し
最後に、更新したロボットの推定状態xEstを保存して、次の時刻t+1に移行して繰り返します。
Out.xDes = [Out.xDes,xDes]; Out.xAct = [Out.xAct,xAct]; Out.xEst = [Out.xEst,xEst];
まとめ
今回の記事では、以前に紹介したカルマンフィルタを用いた移動ロボットの自己位置推定について、シミュレーションで使用したプログラムを紹介しました。
紹介したプログラムは洗練されていないと思いますが、カルマンフィルタの基本式を順に計算していく形になっているので、理解はして頂けるかなと思います。


























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+

Out.xDes = xDes; % Desired Trajectory ←真の値?
Out.xAct = xAct; % Actual Trajectory ←観測値?
Out.xEst = xEst; % Estimated Trajectory ←カルマン?
という認識で合っていますか?
また、
xDes = StateEquation(xDes,u,w*0); % Update Desired State
xAct = StateEquation(xAct,u,w); % Update Actual State
z = OutputEquation(xAct,v); % Get Observation Value
ここでの意味は、実際の観測値がないため、Desが真の値で、それにシステムノイズをのせたものがAct、そしてそれに観測ノイズをのせたものがzということですか?
つまりzには観測ノイズは2つのっているということですか?
コメントありがとうございます。
今回のプログラムで使用した変数(xDes,xAct,xEst)については、下記の通りです。
xDes ← 目標の状態(理想の状態;入力に対するノイズが無く、思った通りに動いた場合の状態)
xAct ← 実際の状態(現実の状態;入力に対するノイズがあるため、思った通りには動かない場合の状態)
xEst ← 推定した状態(観測値を用いて、カルマンフィルタにより推定した状態)
そして、2つの状態xDesとxActのアップデートについて、xDesは目標(理想)の状態なので
xDes = StateEquation(xDes,u,w*0); % Update Desired State
のように雑音部分を0にしています。
そして、xActは実際(現実)の状態なので
xAct = StateEquation(xAct,u,w); % Update Actual State
のようにシステムのノイズwを考慮しています。
また、ロボットの実際の状態はxActなので、観測値を求める際にはxActを用います。
そして、入力と同様に観測した値にも雑音が存在するため、雑音vを考慮して状態xActでの観測値zを求めています。
結果的に、観測値zは入力に対する雑音wを考慮した状態xActでの観測した値に雑音vを考慮しているため、理想値(目標値)から見ると2つのノイズがのっているようにも考えられます。
参考になれば幸いです。