質量‐ばね‐ダンパーシステムを線形微分方程式で表す

今回は、過去に紹介した線形微分方程式（Differential Equation）を用いて、質量‐ばね‐ダンパーシステム（Mass-Spring-Damper System）を表していきます。

質量‐ばね‐ダンパーシステム

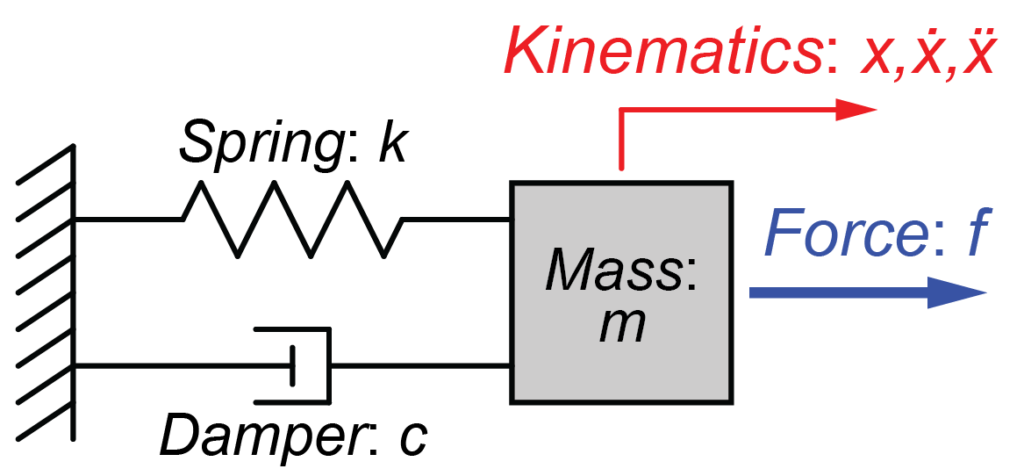
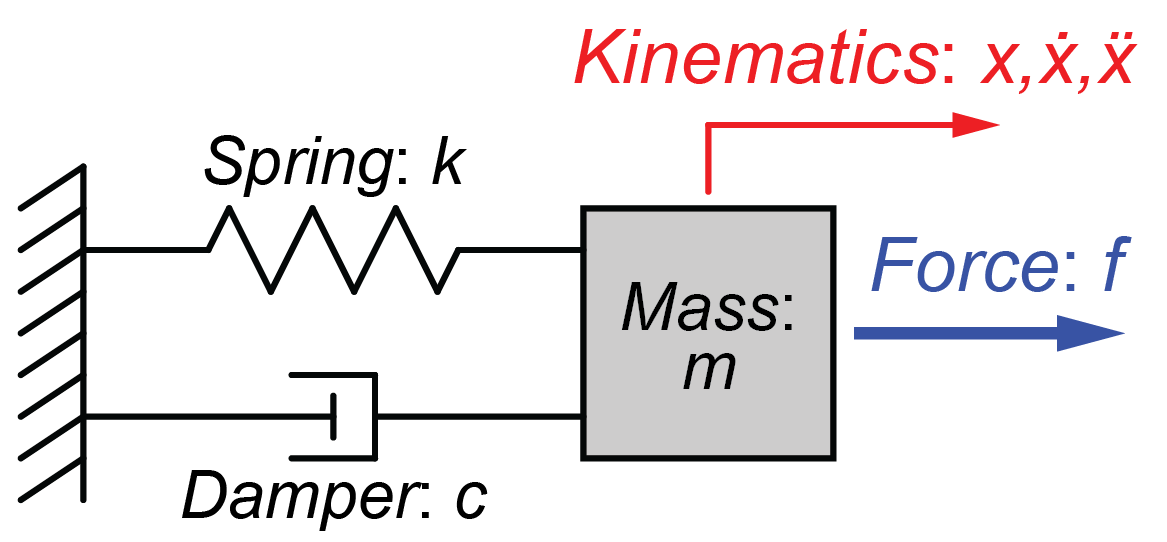
今回扱うシステムモデルは質量\(m\)の左側にばね\(k\)とダンパー\(c\)が取り付けられています。

ばねおよびダンパーの反対側は壁に固定されています。

そして、この右側に力\(f\)を加えた場合の質量の変位\(x\)（及び速度\(\dot{x}\)と加速度\(\ddot{x}\)）を線形微分方程式を用いて表したいと思います。

ニュートンの運動方程式

システムを線形微分方程式で表すために、

$$ F = m a $$

という関係式を使います。

この関係式は、ニュートンの運動方程式というもので、力\(F\)が質量\(m\)と加速度\(a\)の積に等しいということを示しています。

線形微分方程式を使ったシステムモデル

では、今回の質量‐ばね‐ダンパー系の線形微分方程式を考えるために、対象となる質量\(m\)を基準に考えていきます。

質量\(m\)の加速度\(a\)は、

$$ a = \ddot{x} $$

と変位\(x\)の二階微分で求められます。

よって、ニュートンの運動方程式の右辺にあたる質量\(m\)の加速度\(a\)の積は、

$$ m a = m \ddot{x} $$

となります。

次に、質量\(m\)にかかる力を考えていきます。

まず、入力される力\(f\)があります。

この力は変位\(x\)（または加速度\(\ddot{x}\)）と同じ方向に入力されていますので、

$$ F = f $$

とすることが出来ます。

さらにばねとダンパーによる力を考えていきます。

ばねは伸ばされれば縮む方向に縮めれば伸ばす方向に力を発生します。

この時の力の大きさは、$$ F = k x $$と変位\(x\)に比例します。

\(k\)はばね定数で、ばねによって大きさが変わります。

この時の力の向きは変位\(x\)の向きとは逆向きになります。

ダンパーは速度\(\dot{x}\)に対して抑制する向きに力を発生します。

この時の力の大きさは、$$ F = c \dot{x} $$となり、速度\(\dot{x}\)（変位の時間微分）に比例します。

\(c\)はダンパー係数で、ダンパーによって大きさが変わります。

この時の力の向きは速度\(\dot{x}\)の向きとは逆向きになります。

よって、ニュートンの運動方程式の左辺にあたる力の合計は、

$$ F = f – c \dot{x} – k x $$

となります。

以上の結果を組み合わせると、この質量‐ばね‐ダンパー系の線形微分方程式は、

$$ f – c \dot{x} – k x = m \ddot{x} $$

となります。

これを線形微分方程式の基本式のように入力fと出力xで分けて整理すると

$$ m \ddot{x}(t) + c \dot{x}(t) + k x(t) = f(t) $$

となります。

まとめ

このように、質量‐ばね‐ダンパーシステムの入力\(f(t)\)に対する出力\(x(t)\)を線形微分方程式で表すことが出来ました。

次回は、ラプラス変換を用いて伝達関数で表したモデルを紹介したいと思います。